小学数学应用题分类解题大全
求平均数应用题是在“把一个数平均分成几份,求一份是多少”的简单应用题的基础上发展而成的。它的特征是已知几个不相等的数,在总数不变的条件下,通过移多补少,使它们完全相等。最后所求的相等数,就叫做这几个数的平均数。
解答这类问题的关键,在于确定“总数量”和与总数量相对应的“总份数”。
计算方法:
总数量÷总份数=平均数
平均数×总份数=总数量
总数量÷平均数=总份数
例1:东方小学六年级同学分两个组修补图书。第一组28人,平均每人修补图书15本;第二组22人,一共修补图书280本。全班平均每人修补图书多少本?
要求全班平均每人修补图书多少本,需要知道全班修补图书的总本数和全班的总人数。
(15×28+280)÷(28+22)=14本
例2:有水果糖5千克,每千克2.4元;奶糖4千克,每千克3.2元;软糖11千克,每千克4.2元。将这些糖混合成什锦糖。这种糖每千克多少元?
要求什锦糖每千克多少元,要先出这几种糖的总价和总重量最后求得平均数,即每千克什锦糖的价钱。
(2.4×5+3.2×4+4.2×11)÷(5+4+11)=3.55元
例3、要挖一条长1455米的水渠,已经挖了3天,平均每天挖285米,余下的每天挖300米。这条水渠平均每天挖多少米?
已知水渠的总长度,平均每天挖多少米,就要先求出一共挖了多少天。
1455÷(3+(1455-285×3)÷300)=291米
例4、小华的期中考试成绩在外语成绩宣布前,他四门功课的平均分是90分。外语成绩宣布后,他的平均分数下降了2分。小华外语成绩是多少分?
解法一:先求出四门功课的总分,再求出一门功课的的总分,然后求得外语成绩。
(90–2)×5–90×4=80分
例5、甲乙丙三人在银行存款,丙的存款是甲乙两人存款的平均数的1.5倍,甲乙两人存款的和是2400元。甲乙丙三人平均每人存款多少元?
要求甲乙丙三人平均每人存款多少元,先要求得三人存款的总数。
(2400÷2×1.5+2400)÷3=1400元
例6、甲种酒每千克30元,乙种酒每千克24元。现在把甲种酒13千克与乙种酒8千克混合卖出,当剩余1千克时正好获得成本,每千克混合酒售价多少元?
要求每千克混合酒售价多少元,要先求得两种酒的总价钱和两种酒的总千克数。因为当剩余1千克时正好获得成本,所以在总千克数中要减去1千克。
(30×13+24×8)÷(13+8–1)=29.1元
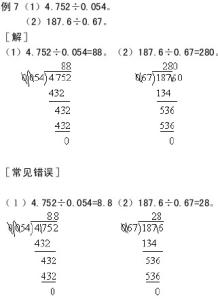
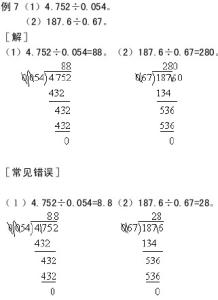
例7、甲乙丙三人各拿出相等的钱去买同样的图书。分配时,甲要22本,乙要23本,丙要30本。因此,丙还给甲13.5元,丙还要还给乙多少元?
先求买来图书如果平均分,每人应得多少本,甲少得了多少本,从而求得每本图书多少元。
1. 平均分,每人应得多少本
(22+23+30)÷3=25本
2. 甲少得了多少本
25–22=3本
3. 乙少得了多少本
25–23=2本
4. 每本图书多少元
13.5÷3=4.5元
5. 丙应还给乙多少元
4.5×2=9元
13.5÷[(22+23+30)÷3–22]×[(22+23+30)÷3–23]=9元
例8、小荣家住山南,小方家住山北。山南的山路长269米,山北的路长370米。小荣从家里出发去小方家,上坡时每分钟走16米,下坡时每分钟走24米。求小荣往返一次的平均速度。
在同样的路程中,由于是下坡的不同,去时的上坡,返回时变成了下坡;去时的下坡,回来时成了上坡,因此,所用的时间也不同。要求往返一次的平均速度,需要先求得往返的总路程和总时间。
1、往返的总路程
(260+370)×2=1260米

2、往返的总时间
(260+370) ÷16+(260+370)÷24=65.625分
3、往返平均速度
1260÷65.625=19.2米
(260+370)×2÷[(260+370) ÷16+(260+370)÷24]=19.2米
例9、草帽厂有两个草帽生产车间,上个月两个车间平均每人生产草帽185顶。已知第一车间有25人,平均每人生产203顶;第二车间平均每人生产草帽170顶,第二车间有多少人?
解法一:
可以用“移多补少获得平均数”的思路来思考。
第一车间平均每人生产数比两个车间平均每人平均数多几顶?203–185=18顶;第一车间有25人,共比按两车间平均生产数计算多多少顶?18×25=450。将这450顶补给第二车间,使得第二车间平均每人生产数达到两个车间的总平均数。
6. 第一车间平均每人生产数比两个车间平均顶数多几顶?
203–185=18顶
7. 第一车间共比按两车间平均数逆运算,多生产多少顶?
18×25=450顶
8. 第二车间平均每人生产数比两个车间平均顶数少几顶?
185–170=15顶
9. 第二车间有多少人、
450÷15=30人
(203–185) ×25÷(185–170) =30人
例10、一辆汽车从甲地开往乙地,去时每小时行45千米,返回时每小时行60千米。往返一次共用了3.5小时。求往返的平均速度。(得数保留一位小数)
解法一:
要求往返的平均速度,要先求得往返的距离和往返的时间。
去时每小时行45千米,1千米要 小时;返回时每小时行60千米,1千米要 小时。往返1千米要( + )小时,进而求得甲乙两地的距离。
1、 甲乙两地的距离
3.5÷( + )=90千米
2、 往返平均速度
90×2÷3.5≈52.4千米
3.5÷( + )×2÷3.5≈52.4千米
解法二:
把甲乙两地的距离看作“1”。往返距离为2个“1”,即1×2=2。去时每千米需 小时,返回时需 小时,最后求得往返的平均速度。
1÷( + )≈51.4千米
 爱华网
爱华网