1962年麦尔齐(Frederick Robertson Macaulay,1882.8.12–1970.3)[1]在对债券价格、债券利息率、到期年限以及到期收益率之间进行了研究后,提出了债券定价的五个定理。至今,这五个定理仍被视为债券定价理论的经典。下面由爱华网小编为你分享债券定价原理的相关内容,希望对大家有所帮助。
债券定价原理是什么
定理一:债券价格与到期收益率
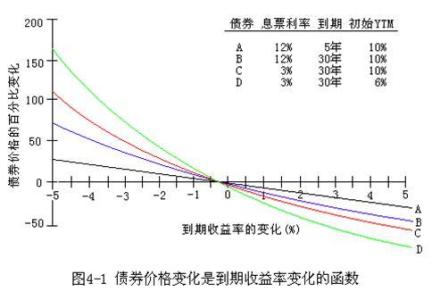
定理一:债券的市场价格与到期收益率呈反向变动关系。(图中,ABCD线都说明了这个反向关系。)
到期收益率上升时,债券价格会下降;反之,到期收益率下降时,债券价格会上升。这一定理对债券投资分析的价值在于,当投资者预测市场利率将要下降时,应及时买入债券,因为利率下降债券价格必然上涨;反之,当预测利率将要上升时,应卖出手中持有的债券,待价格下跌后再买回。
Pv为债券当前市场价格,
F=债券面值
C为按票面利率每年支付的利息
y为到期收益率,到期收益率 (Yield To Maturity,简称YTM),又称“满期收益率”、“到期殖利率”(简称为殖利率)
n为待偿期,也叫剩余到期年限
定理二:债券价格与到期时间
定理二:当债券的收益率不变,即债券的息票率与收益率之间的差额固定不变时,债券的到期时间与债券价格的波动幅度之间成正向变动关系。(比较图中的A线和B线)
即到期时间越长,价格波动幅度越大;反之,到期时间越短,价格波动幅度越小。图中B线到期时间长于A线的到期时间,收益率不变时x固定,B线的价格变动y的绝度值大于A的价格变动y。对投资者而言,如果预测市场利率将下降,在其他条件相同的前提下,应选择离到期日较远的债券投资。
随着债券到期时间的临近,债券价格的波动幅度减少,并且是以递增的速度减少;反之,到期时间越长,债券价格波动幅度增加,并且是以递减的速度增加。
这一定理说明:随着到期日的临近,债券价格对市场利率的敏感度以递增的比率减少。即债券价格的利率敏感性的减少大于相应的债券期限的减少。图中,B线逐渐靠近A线,
这一定理也说明:当到期期限增加时,债券价格对收益变化的敏感性以递减的比率增加,即债券价格的利率敏感性的增加小于相应的债券期限的增加。
定理三:债券价格与债券期限
定理三:长期债券比短期债券具有更强的利率敏感性。(图中,比较A线和B线,再比较A线和BCD线)
即对于等规模的收益变动,长期债券价格的变动幅度大于短期债券。
这一定理也可理解为,若两种债券的其他条件相同,则期限较长的债券销售价格波动较大,债券价格对市场利率变化较敏感;一旦市场利率有所变化,长期债券价格变动幅度大,潜在的收益和风险较大。
随着债券到期时间的临近,债券价格的波动幅度减少,并且是以递增的速度减少;反之,到期时间越长,债券价格波动幅度增加,并且是以递减的速度增加。
定理四:债券价格与市场利率
定理四:债券收益率变化引起的价格变化具有不对称性。(图中,ABCD线都说明了这个不对称性。)
即由收益上升引起的价格下降幅度低于由收益的等规模(相同的基本点)下降引起的价格上升的幅度。
对于期限既定的债券,由收益率下降导致的债券价格上升的幅度大于同等幅度的收益率上升导致的债券价格下降的幅度。
这一定理说明债券价格对市场利率下降的敏感度比利率上升更大,这将帮助投资者在预期债券价格因利率变化而上涨或下跌能带来多少收益时做出较为准确的判断。
即对于同等幅度的收益率变动,收益率下降给投资者带来的利润大于收益率上升给投资者带来的损失。
ABCD线都说明了这个关系:收益率下降a,x为-a,价格变动为Y(-a);收益率上什a,价格变动为Y(a)。Y(-a)的绝对值不等于并且大于Y(a)的绝对值。图示,左边的喇叭口要比右边的喇叭口大。
定理五:债券价格与票面利率
定理五:对于给定的收益率变动幅度,债券的息票率与债券价格的波动幅度之间成反向变动关系(比较图中的B线和C线)。
债券的息票利率越高/低,由收益变动引起的价格变动的百分比越小/大。
也就是说,息票利率较高的债券,其价格的利率敏感性低于息票利率较低的债券。
息票率越高,债券价格的波动幅度越小。图中:B线的息票率高于C线的息票率,在同一x坐标中,但B线y坐标的绝对值小于C线y坐标的绝对值。
这一定理告诉投资者,对于到期日相同且到期收益率也相同的两种债券。如果投资者预测市场利率将下降,则应该选择买入票面利率较低的债券,因为一旦利率下降,这种债券价格上升的幅度较大。如果预测市场利率将上升,则应该选择卖出票面利率较低的债券,因为一旦利率上升,这种债券价格下降的幅度较大。值得注意的是,这一定理不适用于1年期的债券和永久债券。
 爱华网
爱华网