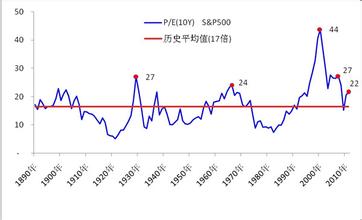
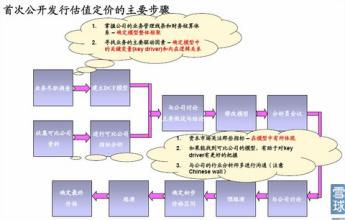
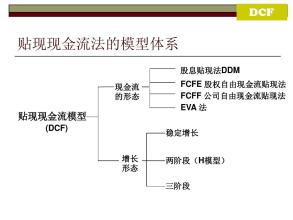
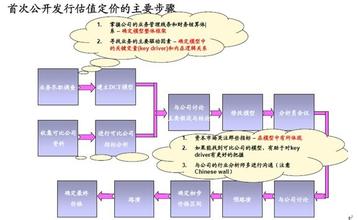
贴现率是指将未来支付改变为现值所使用的利率,或指持票人以没有到期的票据向银行要求兑现,银行将利息先行扣除所使用的利率。这种贴现率也指再贴现率,即各成员银行将已贴现过的票据作担保,作为向中央银行借款时所支付的利息。
一、资本资产定价模型(CAPM)
资本资产定价模型用不可分散化的方差来度量风险,将风险与预期收益联系起来,任何资产不可分散化的风险都可以用β值来描述,并相应地计算出预期收益率。
E(R)=Rf+β(E[Rm]-Rf)
其中:Rf =无风险利率
E(Rm)=市场的预期收益率
投资者所要求的收益率即为贴现率。
因此,从资本资产定价模型公式可以看出,要估算出贴现率要求以下变量是已知的:即期无风险利率(Rf)、市场的预期收益率(E(Rm))、资产的β值。
二、估算无风险利率
无风险利率,是指投资者可以任意借入或者贷出资金的市场利率。现阶段,符合理论要求的无风险利率有两个:回购利率、同业市场拆借利率。
在债券市场发达的国家,无风险利率的选取有三种观点:
第一种观点:用短期国债利率作为无风险利率,用根据短期国债利率计算出的股票市场历史风险溢价收益率作为市场风险溢价收益率的估计值。以这些数据为基础计算股权资本成本,作为未来现金流的贴现率。
第二种观点:用即期短期政府债券与市场的历史风险溢价收益率计算第一期(年)的股权资本成本。同时利用期限结构中的远期利率估计远期的无风险利率,作为未来时期的股权资本成本。
第三种观点:用即期的长期国债利率作为无风险利率,用根据长期国债利率计算出的股票市场历史风险溢价收益率作为市场风险溢价收益率的估计值。以这些数据为基础计算股权资本成本,作为未来现金流的贴现率。
三、估算风险溢价
CAPM中使用的风险溢价是在历史数据的基础上计算出的,风险溢价的定义是:在观测时期内股票的平均收益率与无风险证券平均收益率的差额,即(E[Rm]-Rf)。
对于使用算术平均值还是几何平均值有很大的争论。主张使用算术平均值的人认为算术平均值更加符合CAPM期望一方差的理论框架,并且能对下一期的收益率做-爱华网-出较好的预测。主张使用几何平均值的人认为几何平均值考虑了复利计算方法,是对长期平均收益率的一种较好的估计,这两种方法所得到的溢价利率可能会有很大的差异。
四、估算β值
关于β值的估算,因首次公发与增发项目类型不同估算方法不尽相同。
对于增发项目来说,其已经是上市公司、股票已经上市交易,对其β值估算的一般方法是对股票收益率(R1)与市场收益率(Rm)进行回归分析:R1=a+bRm,其中:a=回归曲线的截距, b=回归曲线的斜率=cov(R1 Rm)/σ2m。

对于首次公发项目,其股票尚未发行上市,无法通过上述估算方法得出β值,需要通过其他方法进行估算。
可比公司法,即利用与该公司经营风险和杠杆比率都具有可比性公司的β值。而后,利用前面讲过的β值与杠杆比率的关系,我们可以进一步根据被评估公司与可比公司之间财务杠杆的差异对β值进行调整。
公司基本因素法,这种估算公司β值的方法是综合考虑行业与公司的基一因素,损益表与资产负债表的一些科目都对β值有很重要的预期作用,高红利支付率表明公司β值较低;公司收益不稳定并且与宏观经济有很大相关性表明公司β值较同。研究人员已经对公司β值与其基本因素之间的关系进行了研究。
据此便可依据资本资产定价模型公式计算出贴现率。
 爱华网
爱华网