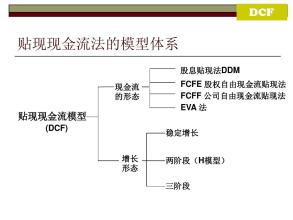
红利贴现模型是股权自由现金流模型的特例, 因为不可能对现金红利做出无限的预测,所以人们根据对未来增长率的不同假设构造出了几种不同形式的红利贴现模型:一阶段红利模型、二阶段红利模型、三阶段红利模型。
一、一般模型
投资者购买股票,通常期望获得两种现金流;持有股票期间的红利和持有股票期末的预期投资股票价格。由于持有期期末股票的预期价格是由股票未来红利决定的,所以股票当前价值应等于无限期红利的现值:
股票每股价值= ∑DPSt/(1+r)t t从1至无穷大。
其中:DPSt=每股预期红利
r=股票的要求收益率
这一模型的理论基础是现值原理——任何资产的价值等于其预期未来全部现金流的现值总和,计算现值的贴现率应与现金流的风险相匹配。
模型有两个基本输入变量:预期红利和投资者要求的股权资本收益率。为得到预期红利,我们可以对预期未来增长率和红利支付率做某些假设。而投资者要求的股权资本收益率是由现金流的风险所决定的,不同模型度量风险的指标各有不同——在资本资产定价模型中是市场的β值,而在套利定价模型和多因素模型中各个因素的β值。
二、稳定增长模型
Gordon增长模型可用来估计处于“稳定状态”的公司的价值,这些公司的红利预计在一段很长的时间内以某一稳定的速度增长。
Gordon增长模型把股票的价值与下一时期的预期红利、股票的要求收益率和预期红利增长率联系起来,
股票的价值=DPS1/(r-g)
其中DPS1=下一年的预期红利
r=投资者要求的股权资本收益率
g=永续的红利增长率
虽然Gordon增长模型是用来估计权益资本价值的一种简单、有效的方法,但是它的运用只限于以一稳定的增长率增长的公司。当我们估计一个“稳定”的增长率时,有两点值得关注:第一、因为公司预期的红利增长率是永久持续下去的,所以公司其他的经营指标(包括净收益)也将预期以同一速度增长。因此,虽然模型只对红利的预期增长率提出要求,但是如果公司真正处于稳定状态,也可以用公司收益的预期增长率来替代预期红利增长率,同样能够得到正确的结果。
Gordon增长模型是对股票进行估价的一种简单而快捷的方法,但是它对选用的增长率特别敏感,当模型选用的增长率收剑于贴现率的时候,计算出的价值会变得无穷大。
三、两阶段红利贴现模型
两阶段增长模型考虑了增长的两个阶段;增长率较高的初始阶段和随后的稳定阶段,在稳定阶段中公司的增长率平稳,并预期长期保持不变。
模型认为公司具有持续n年的超常增长时期和随后的永续稳事实上增长时期;超常增长率;每年g%,持续n年 稳定增长率:gn持续永久。
股票的价值=超常增长阶段股票红利的现值+期末股票价格的现值
P0=ΣDPSt/(1+r)t + Pn/(1+r)n
其中: Pn = DPSn+1/(rn-gn)
DPSt=第t年预期的每股红利
r=超常增长阶段公司的要求收益率(股权资本成本)
pn=第n年末公司的价格
g=前n年的超常增长率
gn=n年后永续增长率
rn=稳定增长阶段公司的要求收益率
在超常增长率(g)和红利支付率在前n年中保持不变的情况下,这一公式可简化如下:
P0 = DPS0(1+g)[1-(1+g)n/(1+r)n]/(r-g) + DPSn+1/[(rn-gn)(1+r)n]
在Gordon增长率模型中对增长率的约束条件同样适用于两阶段增长模型中期末增长率(gn),即公司的稳定增长率和宏观经济名义增长率相当。另外,红利支付率必须与预期增长率相一致。如果预期在超常增长阶段结束后公司增长率大幅下降,则稳定阶段的红利支付率应比超常增长阶段高(一个稳定的公司比一个增长的公司可能将更多的盈利用来发放红利)。一种预测新红利支付率的方法是运用第二讲中描述的基本增长模型。
g=β{ROA+D/E(ROA-i[1-t])}
其中:β=留存比率=1-红利支付率
ROA=资产收益率=(净收润+利息费用[1-t])/总资产
D/E=负债/权益比率(账面值)|!---page split---|
i=利息/负债的账面值
t=所得税率
对这一增长率方程进行变形,我们得到红利支付率与预期增长率的函数关系:
红利支付率=1-β=1-[g/{ROA+D/E(ROA-i[1-t])}]
这一公式的输入变量就是稳定增长阶段要求的输入变量。
两阶段经利贴现模型存在三个问题。第一个问题是如何确定超常增长阶段的长度。由于增长率在这个阶段结束之后预期将降到稳定水平,所以延长这一阶段的时间会导致计算出的价值增加。虽然从理论上,超常增长阶段持续的时间可以和产品生命周期以及存在的项目机会联系在一起,但是把这些定性考虑的因素变成定量化的时间在实践中还是很困难的。
模型的第二个问题在它假设初始阶段的超常增长率很高,而在此阶段结束时的一夜之间就变成较低的稳定增长率。虽然这种增长率的突然转变在实际中可能会发生,但是如果认为从超常增长阶段到稳定增长阶段的增长率变化是随时间逐步发生的,则更符合现实。第三个问题:由于在两阶段模型中最终计算出的价值的一个重要组分部分是超常增长阶段的期末价格,而它又是根据Gordon增长模型计算得出的,所以最终价值对稳定增长阶段的增长率十分敏感。对此阶段增长率的过高或过低预测将可能导致估价结果产生严重的误差。
因为两阶段红利贴现模型基于清晰定义的两个增长阶段——超常增长阶段和稳定增长阶段,所以它最适合于具有下列特征的公司:公司当前处于高增长阶段,并预期在今后一段时期内仍将保持这一较高的增长率,在此之后,支持高增长率的因素消失。例如,模型适用的一种情形是:一家公司拥有一种在未来几年内能够产生出色盈利的产品专利权,在这段时期内,预期公司将实现超常增长;一旦专利到期,预计公司将无法保持超常的增长率,从而进入稳定增长阶段,另一种情形是:一家公司处于一个超常增长的行业,而这个行业之所以能够超常增长,是因为存在着很高的进入壁垒(法律或必要的基础设施所导致的),并预计这一进入壁垒在今后几年内能够继续阻止新的进入者进入该行来。这时,对公司作两阶段增长的假设是合理的。
增长率由初始阶段较高的水平徒然降至稳定增长率水平的假设也暗示着这一模型对那些在最初阶段增长率适中的公司更加适用。例如,假定一家公司在超常增长阶段的增长率为12%,之后,它的增长率降到6%,要比假设一家公司从40%的超常增长阶段陡直降至6%的稳定增长阶段更加合乎情理。
四、H模型
H模型是也是两阶段增长模型,但与传统的两阶段增长模型不同,H模型初始阶段的增长率不是常数,而是随时间线性下降的,直到到达稳定阶段的增长率水平。
模型依据的假设是:收益增长率以一个很高的初始水平开始,在整个超常增长阶段按线性下降(假定持续时间为2H),一直降到稳定增长率(g)。它还假定红利支付率不随时间而发生变化,且不受增长率变化的影响。
H模型中预期红利的价值写为:
P0 = DPS0(1+g)/(r-gn) + DPS0*H(ga-gn)/(r-gn)
其中:P0=当前公司每股股票的价值
DPSt:第t年公司的支付的红利
r=股权投资者要求的市盈率
ga=初始的增长率
ga=2H年年末的增长率,之后永久持续下去
H模型部分地解决了有关增长率从较高水平陡直下降到稳定增长水平的问题,但这样做是有代价的:首先,增长率的下降将按照模型设计的严格过程进行,该模型根据初始增长率、稳定增长率和超常增长阶段的长度,计算得到增长率每年的变化量,增长率按这一变化量以线性的方式下降。如果这一假定与实际情况偏差较小,则对估计结果的影响不大;但是如果偏差较大的话,则可能会引发问题。第二,公司在两个增长阶段红利支付率不变的假设将使分析人员陷入自相矛盾之中——公司增长率下降,而红利支付率保持不变。
增长率随时间线性下降的模型适用于具有下列特征的公司:公司当前的增长率较高,但是当公司规模越来越大时,预期增长率将随时间逐渐下降。与竞争对手相比,这些公司拥有的竞争优势也逐渐丧失。然而,红利支付率是常数的假设使它不适于用在当前红利很低或不支付红利的公司。因此,高增长率和高红利支付率的要求使H模型的应用范围十分有限。
五、三阶段红利贴现模型
三阶段红利贴现模型结合了两阶段模型和H模型的特点。它将公司分为初始的超常增长阶段、增长率下降的过渡阶段和最后的稳定曾长阶段。因为它没有对公司的红利支付率强加任何限制,所以它是最普遍使用的红利贴现模型。
三阶段模型假设公司前后经历三个阶段:保持高增长率的初始阶段、增长率下降的过渡阶段和永续低增长率的稳定增长阶段。公司股票的价值是高增长阶段、过渡阶段的预期红利的现值和最后稳定增长阶段开始时的最终价格的现值的总和。
这一模型与其他类型在红利贴模不同,不存在许多人为强加的限制条件。但是作为代价,它需要数量较多的输入变量——特定年份的红利支付率、增长主经和β值。
三阶段模型的灵活性使它适用于任何一家增长率随时间改变的同时。其他指标——尤其是红利支付政策和风险也将发生改变的公司。而该模型最适合的公司是:当前正以超常的速率增长,并预期在一段初始阶段内将保持这一增长率,前后公司拥有的竞争优势的消失导致增长率逐渐降低,直到稳定增长阶段的水平。
 爱华网
爱华网