函数的零点是函数图象与X轴交点的横坐标,即方程f(x)=0的解。它是一个数而不是点的坐标。是新课标的新增内容,也是高考的热点。要求学生能够结合函数的图象,理解函数的零点与方程的根的联系,转化为判断方程根的存在性及根的个数。下面就函数零点试题常见类型进行解析。 1.函数零点求解方法 把求函数零点问题转化为方程的实数解问题,求方程的实数解。 求下列函数零点 f(x)=x3-2x2-x+2 f(x)=x- 解析:(1)由x3-2x2-x+2=0得x2(x-2) -(x-2)=0 ∴ (x-2)(x+1)(x-1)=0 ∴ x=2或x=1或x=-1 ∴ 函数f(x)的零点是2,1,-1 (2)由x-=0得=0 ∴ (x-2) (x+2)=0 ∴ x=2或x=-2 ∴ 函数f(x)的零点是2或-2 点评:求函数f(x)的零点,转化为方程f(x)=0,通过因式分解把方程转化为一次方程或二次方程再求解。 2.函数零点所在区间的判断 用零点存在性定理判断零点所在的区间或通过函数图象及函数的性质进行判断。 例2. (1) 函数f(x)=2x+3x零点落在的一个区间是( ) A.(-2,-1) B.(-1,0) C.(0,1) D.(1,2) (2) 函数f(x)= -cosx在[0,+∞)内( ) A. 没有零点 B.有且仅有一个零点 C.有且仅有两个零点 D.有无穷多个零点 解析:(1)f(-1)= -<0 , f(0)=1>0 函数y=2x, y=3x在(-∞,+∞)均为增函数,∴f(x)=2x+3x在(-∞,+∞)是增函数 。 ∴f(x)在(-1,0)内有一零点。所以选B。 (2)在同一坐标系中分别作出函数y=和y=cosx的图象,如图: 当x>1时,y=>1, y=cosx≤1, ∴两图象只有一个交点,即方程-cosx=0在[0,+∞)只有一个实数解。 ∴f(x)= -cosx在[0,+∞)内只有一个零点 所以选B。 点评:(1)运用零点存在性定理判断零点所在区间,必须结合端点函数值的符号和单调性。 (2)运用图象进行判断,要求学生能够熟练掌握基本初等函数的图象。 3.函数零点个数的判断 函数f(x)在某区间上是否有零点,有几个零点通常用下列方法进行判断:(1)通过解方程判断函数零点个数,(2)利用零点存在定理判断,(3)利用图象法转化为求两个函数图象交点的个数问题进行判断。 例3. (1) 函数f(x)= 的零点的个数为( ) A.0 B. 1 C. 2 D. 3 (2) 函数f(x)=4x3+x-15在[0,2]上的零点的个数为______ (3) 函数f(x)=2-x+x2-3的零点个数为______ 解析:① 由 得x=-3, 由 得x=e2 ∴f(x)的零点个数为2,故选C ② ∵函数y=4x3 和y= x-15在[1,2]上为增函数,∴函数f(x)=4x3+x-15在[1,2]上为增函数。 ∵f (0)=-15, f(1)=-10<0,f(2)=19>0 ∵f(x)=4x3+x-15在[1,2]内存在一个零点 ③ 分别作出函数f(x)=3-2-x 与函数g(x)= x2 的图象 ∵ f(0)=2,g(0)=0 ∵ 从图象上可以看出它们有2个交点,函数f(x)=2-x+x2-3的零点个数为2。 点评:用解方程确定零点个数要注意函数定义域,用零点存在性定理判定,需将判定的区间划分为函数的单调区间逐一判定,借助基本函数图象判定零点个数是常用方法之一。 4.用二分法求零点的近似值 二分法是求方程函数零点的近似值的一种常用方法,通过不断“取中点”来逐步缩小零点所在范围,达到求函数零点的近似值。 例4、若函数f(x)=x3+x2-2x-2的一个正数零点附近的函数值,用二分法计算,其参考数据如下: f(1)=-2 f(1.5)=0.625 f(1.25)=- 0.984 f(1.375)=-0.260 f(1.4375)=0.162f(1.40625)=- 0.054 则方程x3+x2-2x-2=0的一个近似解(精确到0.1)为______ A.1.2 B. 1.3 C. 1.4 D. 1.5 解析:C f(1.40625)=- 0.054<0 , f(1.4375)=0.162>0且都接近0,由二分法可知其根近似值为1.4,故选C。 点评:二分法的思想方法是一种可用计算机求方程近似解的方法,也是求零点近似解编程的基本依据。 5.函数零点的应用 (1)若方程是一元二次方程,利用方程根与系数的关系或数形结合求解。 若非一元二次方程,则构造函数,利用函数图象求解。 例5、(1)已知函数f(x)= x2+(a2-1)x+a-2的一个零点比1大,一个零点比1小,求实数a的取值范围。 解析:方法一:设方程f(x)=0两个根为x1, x2 (x1 则(x1-1)( x2-1)<0 ∴x1x2-(x1+x2)+1<0 由根与系数的关系得到 即a2+a-2<0 ∴ -2 ∴a的取值范围是(-2,1)
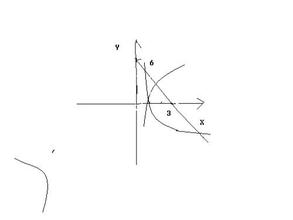
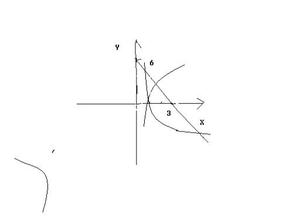
方法二:函数的大致图象如图: 则f(1)<0 即1+(a2-1)+(a-2)<0 得: a2+a-2<0 ∴ -2 ∴ a的取值范围是(-2,1) (2)已知函数f(x)=-x2+2ex+m-1 g(x)= x+(x>0),m取何值时,方程g(x)-f(x)=0有两个相异实根。 解析:方程g(x)-f(x)=0有两个相异实根,即g(x)=f(x)中g(x)和f(x)图象有两个不同交点。 对于函数,g(x)= x+ (x>0) =1- =1-≥0 得 x≥e, 故函数g(x)单调递增区间为[e,﹢∞) 由= 1-≤0 得0<x≤e,故函数g(x)单调递减区间为(0,e] ∴ x=e时,g(x)有最小值2e 对于函数f(x)=- x2+2ex+m-1=-(x-e)2 + m-1+e2为开口向下的抛物线,对称轴为x=e,最大值为m-1+e2 ∴ 当2e<m-1+e2 即 ∴ m>- e2+2e+1时,f(x)与g(x)有两个不同交点 ∴方程g(x)-f(x)=0有两个相异实根 ∴ m的取值范围是(- e2+2e+1, ﹢∞) 点评:利用零点的问题确定函数中参数的取值,是有关函数、方程、不等式的综合性问题。解决问题的主要思想方法是分类讨论与数形结合。特别是有关二次函数解析式中参数的取值范围的讨论。充分利用根与系数的关系,对称轴与零点关系,最值与零点的关系。
 爱华网
爱华网