经济批量概念的价值在制造控制的分析中,通常把自然地落入同一组类的物品放在一起研究是方便与实际的。这些组类可以是同一些制造设备所加工的零件组成,或由同一采购员办理的采购物品组成,或由从同一供应商订货的物品组成。在确定采购物品的批量时特别适用。当考虑相关零件的系列时,成本、资金需求、空间需求、作业条件及确定批量时必须考虑的其它因素最有意义。在批量计算的首例中,有5个物品。这些物品可想象为在同一设备上制造的产品。图所示为现状,批量根据经验确定,每季度运行一次,这是非专业人员时常采用的具有代表性的直觉法则。物 品 年使用金额 目前年订货次数 目前订货量───────────────────────────────────1 ¥10,000 4 ¥2,5002 6,400 4 1,6003 2,500 4 6254 400 4 1005 144 4 36───────────────────────────────────总计 20 ¥4,861平均批量库存 = ¥2,430经验批量对每种物品一年做4次生产调整或订货,总计每年有20份订单;平均批量库存等于批量库存总计的二分之一,即¥2430。这是假设每批都是收进一整批货然后在一段时间内均匀地使用,直到库存降为零,因此平均批量库存为批量的一半。显然,倘若把物品5的若干次生产调整转用于物品1,就可显著地压缩库存。即使一次生产出全年度的物品5,对库存投资也无多大影响,而对于物品1每多作一次生产调整却可减少相当多的库存。图所示为重新分配这20次生产调整后的情形。其结果是每年总的订货次数没有变,但平均批量库存由¥2430降到了¥1828。物 品 年使用金额 建议的年订货次数 建议的订货量───────────────────────────────────1 ¥10,000 10 ¥1,0002 6,400 5 1,2803 2,500 3 833 4 400 1 4005 144 1 144──────────────────────────────────总计 20 ¥3,657平均批量库存 = ¥1,828生产调整的经济使用原理6.把生产调整次数分配给高值物品以降低其库存,可轻而易举地补偿低值物品库存的增长。用目视法作这类分析只有在物品数很小时才实用。有时对一些由关键工作中心制造的关键物品使用这种普通方法就可作出显著改进。虽然所得的订货量尚非经济订货量(因为未考虑库存持有成本、生产调整或订货成本),但它们比原来的订货量要合理些。使用它们将降低同持有成本相关的一切费用而并不影响同订货有关的成本。在许多公司里──特别是从制造厂家购进货物然后销售给零售商的批发仓库──多年来通常使用这样的制度:每隔2或3个月审查一次全部产品并将它们全部同时重新订货,而且其订货量以供应时间计算是相等的(譬如每种物品2个月的供应量)。当联合采购所有物品可享受折扣时,这种办法是有点道理的,但这类重新订货的体制时常只是由于它看起来似乎有道理就被采用了。例如第二章中所举的60天订货法则与图凭目视法作出的改进都是非专业方法的适例。它们都不是经济解;有更好的重新分配生产调整或重新订货的办法可以显著地改进公司资源的使用。所示的办法是否每年作20次生产调整的最优分配法?实际上它不是的。有一种简单的数学方法可以得出订货的更好分配法。在研究这种计算法之前,首先要懂得EOQ(Economic Order Quantity)即经济订货量的概念。在许多情况下EOQ概念是没有价值的。在下列情况下计算EOQ是没有理由的,当1、客户规定了数量(即,对于订货生产物品)2、生产运行批量受设备能力限制(例如精细化工产品)。3、产品的货架寿命是短促的。4、工具寿命或需要磨刀、修饰等等、限制了运行时间。5、原料的批量限死了订货量。EOQ的基本概念在库存管理中必须作出的基本决定之一就是对照发出重新补充库存的订单的成本平衡库存投资的成本。要回答的问题是,应该订多少货。正确的订货数量要使同发出订单的次数有关的成本与同所发订单的订货量有关的成本达到最好的平衡。当这两种成本恰当地平衡时,总成本最小。这时所得的订货量就叫做经济批量或经济订货量(EOQ)。EOQ概念适用于下列情况:1、该物品成批地,或通过采购或通过制造而得到补充,它不是连续地生产出来的。2、销售或使用的速率是均匀的,而且同该物品的正常生产速率相比是低的,使得显著数量的库存因而产生。EOQ概念并不适用于为库存而生产的一切物品。例如,在一家精炼厂或一条装配线上,生产是连续的而且不存在这样的批量。在一家订货生产工厂里大多数工作是按客户订货的批量生产的。工具寿命有限、货架寿命短、原料的经济使用和其它约束压倒了EOQ技法的应用。尽管如此,这一概念在工业界仍有广泛的应用,因为大多数生产不是连续式的而是从一个库存取出一批一批的物料进行加工,然后送交另一库存。在一个制造组织中去区分经济的制造批量与移动批量是重要的。移动批量通常由容器尺寸或货盘容量确定,它可以是经济批量的一小部份。管好制造批量与采购批量这二者是必不可少的,因为它们往往代表库存的最大的单独起作用的部份。确定批量的技法是这类管理工作的良好工具,但专业的实际工作者知道它们的应用实际上只是在一种恶劣情况下求其尽可能地好而已。当生产调整成本或订货成本高时,EOQ引进订货成本与库存持有成本的平衡使总成本最小。但若能压低生产调整或订货的成本,则可以实现更好的结果,加上某些巨大的额外利益。原理7.正确的EOQ是好的,但更短的生产调整比它要好得多。独立地工作时,物料控制人员可选用批量确定技法并应用它们为公司取得某些好处。同主管人员、工具设计者、制造与设计工程师与工人集体合作时,这些人员通过缩短生产调整时间可以产生比这些利益大许多倍的利益。日本人已不容置疑地证明了这一点。试错法在选用批量时有哪些备选方案呢?假设工厂制造订单授权本厂的工人去制造一种标准的存货物品。可以发一份补货订单去生产全年的需求量。这意味着工厂在该年度将只需为制造物品作一次生产调整。也意味着平均批量库存很大,如果使用率是均匀的,它将等于半年的需求量。倘若一年中订货50次──接近于每周一次──就可大大削减这一年平均批量库存。但将给该厂加上一个很重的负担,因为这项工作要作50次生产调整才能完成全年的需求量。这两种极端的方案所示。在确定经济批量时必年需求量=¥1,000产值─────────────────────每年补货次数 批量 平均批量库存1 ¥1,000 ¥50050 20 10─────────────────────须面临的基本的两难问题是:不频繁地订货可使订货或生产调整成本下降但带来的库存投资将很高;频繁地订货可使库存降低但带来的订货成本将很高。确定经济批量要求找出能使总成本即二者之和最小的那个订货量。例如,设发一份补货订单的成本是¥10(如果只考虑付现成本,这可以是实际的;本例的成本数据并非旨在表现实际成本而是为了说明如何计算,说明其中的关系)。再设库存持有成本等于每年库存投资金额平均值的20%。可用试错法来确定经济批量,如图所示。如果此物品的年度使用量值¥1000,
订货成本=¥10
年使用金额=¥1,000库存持有成本=20%───────────────────────────────────订货量 平均库存 持有成本 年订货次数 订货成本 总成本───────────────────────────────────¥ 50 25 ¥ 5 20 ¥200 ¥205100 50 10 10 100 110200 100 20 5 50 70250 125 25 4 40 65500 250 50 2 20 70───────────────────────────────────试错计算法
每次订货量为¥50,则平均批量库存将为¥25;年持有成本将为¥25的20%即¥5;年订货次数为20,每次¥10,年订货成本为¥200;总成本将为¥205,等于¥200订货成本与¥5持有成本之和。订货量加大时,平均库存随之增大,其结果是库存持有成本增大。订货量较大时,年订货次数减少,使订货成本下降。注意最右一列其标题是“总成本”。可以看出总成本最低是在订货量为¥250元之时。这就是能使订货成本与持有成本“相平衡”的订货量;它是该物品的EOQ。随着订货量增大,持有成本上升而订货成本下降。上面的曲线是总成本曲线,随着订货量的增大它在订货量为¥250时降到最低点;再增大订货量时总成本反而上升,然而要注意这增量是相对地小的。订货量大于EOQ时,其惩罚要远小于订货量小于EOQ的时候。然而要记住,这里只考虑了订货成本与持有成本。在库存控制中这是一个有用的概念,它比凭直觉的“猜测”能够导至可观的节约。订货量为¥250时的总成本比订货量¥50时总成本的一半还要小。无精确成本时的EOQ在前述例子中,假定订货成本与持有成本的精确数值是已知的。每一个EOQ公式都是这样假设的。实际应用时,这些成本是难以准确地确定的(理由见本章后面)实际工作者不应由于缺乏精确成本数据而泄气以致不去通过使用EOQ寻找可能的节约。无论如何,由于下述两个原因,使用经济批量概念是可以给生产控制带来实际好处的。1、根据一贯而有序的方法所确定的订货量比凭经验或猜测确定的订货量,其结果要好得多。几乎总是可以比直觉批量作出改进。2、总成本曲线(见图3-5)在EOQ的两边都有一相当宽的扁平区。这说明即便使用被认为远非完善的成本数据也可以找出相当经济的订货量。也说明可以修改从公式计算出来的订货量而不致于牺牲显著的节约(例如不妨将公式算出的EOQ=1910取整数成为更切合实际的2000)。平方根EOQ在工业界,采用试错法去求库存中成千种物品的经济批量是不切实际的。有若干公式可用来计算任一物品的EOQ。最早的形式是─────EOQ=√2AS/I 其中 A=年度使用量,用金额(元)表示S=生产调整或订货成本(元)I=库存持有成本,用每元平均库存的小数表示把数据代入此式,可算出──────────────EOQ=√2×1000×10/0.20───────=√100,000=¥316注意此公式给出了比试错法计算得更精确的答案。它是否更经济?(3-1)式是通过解出库存持有成本方程与订货成本方程去找出最低总成本从而推导出来的,详见附录Ⅱ。换句话说,此公式找出了总成本曲线的最低点,它比选出的值稍有不同。EOQ公式(3-1)包括两个成本因素:生产调整或订货成本S与库存持有成本I。对一个物品系列,通常库存持有成本假设对所有物品都相同,而生产调整或订货成本对该组物品往往实际上是相同的。如果上述成立,公式(3-1)可写成:──── ─ ─EOQ=√2S/I × √A=K×√A 其中 ────K=√2S/I公式指出一个非常有用的关系:最经济的批量是年使用量金额的平方根的函数。
现在可以用公式计算出5种物品的经济批量,所示。─ 计算所得物品 年使用金额 √A 目前年订货 目前订货量 年订货次数 订货量A 次数N───────────────────────────────────1 ¥10,000 ¥100 4 ¥2,500 7.6 ¥1,3102 6,400 80 4 1,600 6.2 1,0503 2,500 50 4 625 3.8 6554 400 20 4 100 1.5 2625 144 12 4 36 0.9 157───────────────────────────────────262 20 ¥4,861 20.0 ¥3,434平均批量库存 ¥2,430 ¥1,717给定总订货次数条件下的最低库存计算中要用到的20次订货的K值可从公式(3-3)导出的另一关系式求得,即
──∑√A 262K=──────=────=13.1 (3-4)∑ N 20─在此公式中,所有物品的年使用量平方根之和(∑√A)除以目前这些物品每年订货的总次数(∑N)就得到K值。已知K值,则使用公式(3-2)立即可以算出每一物品的EOQ,最右一列所示。当每年共发出20份订单时,¥1,717这个平均批量库存就是这组物品的最低总批量库存。计算此值无需知道订货成本与库存持有成本的具体值。对于实际工作者而言,每年7.6次订货这个概念是令人恼火的,因为0.6次生产调整是无实际意义的。然而,订货量为¥1310───它很可能将四舍五入为¥1300───对于物品1是有效的。在实际工厂里,它将成为某些年份订7次,其它年份订8次。虽然分数的生产调整不实际,但在作批量计算中是方便的,因为如此便可始终使用1年为期间以便比较各项成本。这种方法也可用来计算给定平均批量库存条件下的最少总订货次数,计算方法是使用公式:∑Q 4861K=──────=─────=18.55 ── 262∑√A其中,∑Q是目前各物品订货量之和。─物品 年使用金额 √A 目前年订货 目前订货量 计算所得A 次数 Q 年订货次数 订货量───────────────────────────────────1 ¥10,000 100 4 ¥2,500 5.4 ¥1,8552 6,400 80 4 1,600 4.4 1,4843 2,500 50 4 625 2.7 9284 400 20 4 100 1.1 3715 144 12 4 36 0.7 223───────────────────────────────────262 20 ¥4,861 14.3 ¥4,861平均批量库存 ¥2,430 ¥2,430库存的最少订货次数再次使用公式,可算出每种物品的新的批量而无需知道订货成本与库存持有成本的具体值。对本例中这一系列物品,若给定的平均批量库存为¥2430,可算出最低订货次数为每年14.3次。计算K值的公式首先是由W.Event Welch提出的(9) ,这是尝试计算总量批量库存的第一次。这一EOQ计算方法有5个显著优点:1、对于生产调整(或订货)成本与库存持有成本都差不多相同的一个物品系列,它提供一种简化得多的EOQ计算方法。首先一次性地计算出所有这些物品适用的K值,然后分别乘以每一物品年使用金额的平方根,就可算出其EOQ。例见下一节。2、如果当前的组织其订单处理能力有限,则此法可用来计算受此约束的物品系列的最小总批量库存,3、如果库存量不能被增大到EOQ所要求的程度,则此法可用来确定受此条件约束时的批量使得总的订货次数为最少也就是订货成本最小,4、此法说明把EOQ概念应用到过去靠直觉手段来确定订货量的场合,可以得到若干立竿见影的好处。如前所述,保持订货成本不变时可使库存降低,或保持库存不变时可使订货成本降低。5、此计算方法说明一个非常重要的问题:当物品成组研究时,EOQ的应用要有效得多。人们往往忽视了这一点。虽然应用Welch法时不需知道订货成本与库存持有成本的具体值, 但必须作出基本假设,即他们对系列中每一物品都是相同的。此外,当考虑实际成本时,计算结果未必就是最经济的,如果能获得代表性的成本数据,可能作出更进一步的改进。在实际应用中,其它制约条件可能使得EOQ的全部好处实际上不能立即得到。这些制约条件有:缺乏可用于库存投资的资金,可用来存贮库存的空间有限,有技术的生产调整人员太少,可用于生产调整的机器能力有限。在诸如此类条件下如何能获得EOQ概念的充分发挥,有一种叫做(批量库存管理内插技法)LIMIT的技法可用。 它使我们能够研究在这类约束条件下可以平衡订货成本与库存持有成本的各种备选方案。EOQ公式中的成本毫无疑问,应用EOQ概念时最难办的问题是公式中假设实际的付现库存费用与持有的库存量之间存在着正比关系,并且实际的总订货费用与发生订单数之间也存在着正比关系。而实际上,减少采购订单的数目不见得就会使订货成本成正比地下降。真相是成本与订货量之间的关系并非正比而是阶跃式的。这些阶梯由总量效应控制───诸如要发出的订单的总数以及所需的总的存贮空间───而不是由个别物品的批量来控制的。因此有必要研究整个库存。在II中所给出的库存决策中用来确定成本的两条法则特别适用于经济批量式中使用的成本:1、成本应该是真正取决于所选订货量的那些付现成本。2、成本应该是真正要受订货量大小影响的那些成本。不幸的是,大多数公司会计记录中的成本难得可以直接用于经济批量的计算。EOQ公式中的单价就是这类问题的适例。在许多公司里,一物品的单价往往就是指其“标准成本”,它包括劳务、物料与一切制造作业的间接管理费,其中包括一些用于生产调整的折让。在EOQ公式中确定使用什么单价有两个明显的选择:1、使用标准成本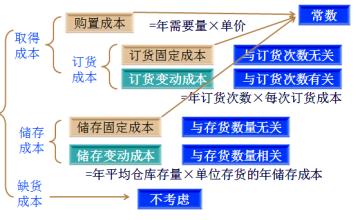
2、只使用标准成本中的劳务与物料部份加上某些随批量而变化的间接费用。如果使用全额标准成本,将违反前述的关于成本的两条法则(因为标准成本的间接部份并不取决于,因而很少受批量改变的影响)。例如,批量库存有所增加时,对大多数间接因素而言,诸如工厂文书性开支、监工开支、设备折旧、检查等等,并不真正要求付现成本有多大增加。倘若用标准成本来推测增加库存将支出的金额,必将失之过大,因为按比例增加的开支将是劳务与物料而非间接费。而且标准成本中通常包括生产调整费用,它在公式中已单独列为一个成本要素,不应再包括在所使用的单价之内。另一方面,会计记录将按标准成本中规定的间接费率来收取库存的间接费。在公式中使用只包括劳务、物料与间接成本可变部份的单价将使计算出的EOQ总库存金额与会计数字不相符合。例如,根据EOQ公式中使用的成本予测出库存将增加¥100,000,这一结果可能引起有关管理人员真正的惊奇,因为会计记录当然将按包括间接费用在内的全额标准成本来计算库存金额,该帐面数字可能指出库存将增加¥150,000而不是前面所予测的¥100,000。使用成本时另一常遇问题发生在小批量物品上。当运行具有高生产调整成本的小批量物品的一次大量供应时,它是按标准成本登入库存金额记录中的。如果在同一次机器调整上使生产量加倍,则遭受报废风险的库存值将无疑要增大,但通常其增量并没有会计记录所指示的那么多。在同一次生产调整上再运行一次额外的供应实际上将只会使物料、劳务与一部份间接费按比例增加。有时,在某些半自动设备上,即使劳务成本也不会按比例增加。然而在库存记录上却按全额标准成本记帐──最后也是按此冲帐。如何处理这一两难问题?只有采用讲两种成本语言的办法。一种是真正的付现成本,它真正地影响着决策───用于计算。同时公司的管理者必须意识到库存中一个给定的变化将会对使用另一种语言的会计记录产生什么影响,因为绩效通常是根据这些记录来评价的。在许多公司里,作业人员与会计人员正试图设计出互相满意的成本核算技法。在此期间,作出作业决策的人员必须去做下列:1、了解公司的成本核算制并同公司财务人员密切合作,使得成本被明智地用于作出决策并向管理者提出备选方案。2、在大规模地使用EOQ之前,必先做试点的应用,并根据样本的结果予测EOQ应用对总库存的影响。平方根EOQ公式的变体捷径:上一节讲过对于成组物品当组内每一物品的生产调整或订货成本与库存持有成本均相同时,可用公式(3-2)中的K来简化EOQ的计算。使用公────式(3-3),K=√2S/I立即可算出K值。然后用公式(3-2),EO─Q=K×√A就可算出每一物品的EOQ。例如:────────────────────────────────物品1 物品2 物品3────────────────────────────────年使用量A ¥10,000 ¥20,000 ¥30,000订货成本S 5 5 5库存持有成本I 0.2 0.2 0.2────────────────────────────────据此可算出K与EOQ──── ───────K=√2S/I=√2×5/0.2=7.07─ ─EOQ=K×√A=7.07×√A─────对物品1,EOQ=7.07×√10000=¥707─────对物品2,EOQ=7.07×√20000=¥1000─────对物品3,EOQ=7.07×√30000=¥1225这种快速算法可大大加快EOQ的计算。当EOQ用件数表示时,可用下式────| 2USEOQ= | ──── (3-6)√ IC其中 U=年使用量(件)S=订货或生产调整成本(元)I=库存持有成本(小数)C=单价 (元/件)非即时收货有时整个批量并非即时收入存货。 制造速率可能使得整个批量要化若干天甚至若干星期才能完成并交到存货。当生产正在进行时,有部份产品送到存货但在此期间也有往外的提货发生。其结果平均批量库存将不等于批量的一半。这种情形叫非即时收货,可用基本EOQ公式的如下修正形式:────────| 2ASEOQ= |──────── (3-7)√I(1-s/p)其中 A=年使用量金额(元)S=生产调整或订货成本(元)I=库存持有成本 (小数)s=使用率,其单位同生产率p=生产率,其单位同使用率注意用此公式计算出的EOQ将大于从假设收货是即时的(3-1)式计算出的EOQ。就是说,非即时收货时,制造批量要加大些,但平均批量库存并不加大,因为当批的余量还在生产时,同时有物料要被提走。即时收货时,库存一下子升高到顶点,然后逐渐使用掉,如图中虚线构成的直角三角形所示。非即时收货时,直到全部收完一批订货也达不到原来的最高点,锯齿形曲线中的三角形不再是直角三角形。主调整与次调整当以一确定的顺序运行成组的物品为最经济时, 主次生产调整是在EOQ的工业应用中常遇的一种情形。例如在自动机床上生产物品时,依次地运行若干相似物品往往是经济的,因为在作好基础的生产调整之后,按照一定顺序每更换一种产品只需作一些次要的调整即可。在轧制薄板时也往往有这种情形。在造纸、化工涂料、化妆品与其它类似的过程工业中,清洗设备是耗时又费钱的,往往先做浅色的,然后依次做越来越深一些的颜色,在最深色处理完毕后再把整条加工线关车、清洗、重新转换。EOQ的基本方法仍适用这些情况,但需对数据作些特殊处理。图3-9所示为一次主生产调整可用于五种物品的一例。此例中,设库存持有成本为库存金物品 年使用量金额 A 生产调整成本 S─────────────────────────────1 ¥ 2,000 ¥ 2.002 4,000 3.003 800 3.004 10,000 2.005 900 2.00──── ────── ───────¥12.00 次调整总额¥50.00 主调整总额系列总计 ¥17,700 ¥62.00图3-9 主调整与次调整额的20%,而每种物品的调整成本如图中所列。除了每一物品的调整成本S之外,还有一笔主调整成本¥50,因此总调整成本为¥62,可用稍加修改的标准EOQ公式(3-8)来处理此问题─────────EOQ = √2×∑A×∑S/I (3-8)其中 ∑A =所有物品年使用量的总和∑S =所有物品调整费的总和其它因素同公式(3-1)。本例中───────────────EOQ =√2×17,700×62/0.2=¥3300即每作一次生产调整后,应依次加工总值为¥3300的这五种物品。可用(3-1)式算出每一物品的相应批量,但这并无实用价值。主要目的应是使每种物品的库存所负担的使用期相等,使得再次做主调整时,所有物品都需投入新的一批。倘若各物品的库存相互之间平衡得很差以致其中的一种用完得比其余的要快许多,就会使人感到很不方便。计算所得的各物品的EOQ是随其使用量的平方根而变的,常用的物品将比慢移物品用完得快。恰当的解法是使每一物品的可供应天数相等,这叫做等耗尽时间法。它是假定按每一物品的平均使用量可以供应相等的天数。更加精细的计算要把可能的误差都估计进去以加大使所有物品同时用完的机会。物品 现有库存 日使用率(每年以250天计)───────────────────────────1 ¥ 336 ¥ 8.002 320 16.003 100 3.204 600 40.005 97 3.60───────────────────────────总 计 ¥1,453 ¥70.80
图3-10 系列物品的现有库存
图3-10所示为每种物品的现有库存与平均日使用量,它等于年使用量除以全年的工作日数。计算步骤是首先计算一轮新的运行使库存骤增后的总库存量。由于该系列物品的批量是¥3300,所以此时的总库存量将为¥3300+¥1453=¥4753。倘若所有物品的库存完全平衡,将可供应¥4753/¥70.80=67天。就是说每一物品的批量应该使它的现有库存在一轮运行之后增加到67天的供应量。如图3-11所示,每一物品67天的供应量减去现有库存,就得到批生产量。物品 67天的供应量 现有库存 批生产量─────────────────────────────1 ¥ 536 ¥336 ¥ 2002 1,072 320 7523 214 100 1144 2,690 600 2,0905 241 97 144──────────────────────────────总计 ¥4,753 ¥1,453 ¥3,300图3-11 系列物品的批量──即时收货此例中,用的是基本EOQ公式(3-8)。当这样的成组物品被运行时,该生产运行可能需要相当长的一段时间。果真如此,则应用非即时收货公式(3-7)将更为恰当,如图3-12所示。计算结果是当这组物品被运行时,此成组物品的物品 A S 日使用率s 日生产率p────────────────────────────────1 ¥ 2,000 ¥ 2.00 ¥ 8.00 ¥602 4,000 3.00 16.00 803 800 3.00 3.20 754 10,000 2.00 40.00 705 900 2.00 3.60 69主调整 50.00────────────────────────────────总计 ¥17,700 ¥62.00 ¥70.80 ¥354图3-12 系列物品的批量──非即时收货─────────EOQ=√2×A×s/I(1-S/p)───────────────=√2×17,700×62/0.2(1-70.8/354)=¥3700批量应等于¥3700,它比即时收货时的批量¥3300要大些。其中每一物品的批量应使所有物品的库存具有相等的可供应天数。注意,哪个物品先做,并无什么要求。如果没有类似颜色由浅到深这样的重要考虑,则应该先做最有可能被用完以致引起缺货的物品。数量折扣采购物料时,供应商往往给购买较大批量的买主以一定的优惠,即可以提供折扣。在下述例中:年使用量=¥10,000订货成本=¥ 5.00库存持有成本=20%使用公式(3-1),可知EOQ=¥707。如果供应商对¥2000以上的批量可提供1%的折扣,则可用列表比较的方法来确定全年的供应总成本,如图3─13所示。左边的数字表明对于计算所得的EOQ,年供应总成本是¥141.10EOQ(无折扣) 大批量(有折扣)────────────────────────────────────¥707 批量 (¥2,000-1%=)¥1,980¥353 平均批量库存 990¥70.60 库存持有成本(20%) ¥19814.1 每年订货次数 5¥70.50 订货成本(每次¥5) + 25──── 折扣的节约 (1%×10,000=) -100 ───¥141.10 全年供应总成本 ¥123────────────────────────────────────图3-13 有采购折扣时的EOQ
有折扣时,批量为¥2,000(1-1%)=¥1,980,平均批量库存为
¥990,库存持有成本为¥198,加上全年订货5次的订货成本为¥25,以上小计达¥223。但1%的折扣使单价下降,全年可节支¥100,故实际上全年供应总成本是¥123。说明接收折扣,加大采购批量是有利的。这一点正是标准EOQ公式中未加考虑的。折扣问题的特征如下:1、为了获取折扣,必须以较大批量采购;其结果是库存与库存持有成本将会上升。2、以较大批量订货可减少订货次数使总的订货成本下降,这通常在总数上不是一个大的因素(注意较大的批量也减少缺货从而减少了安全存货的需要)。3、折扣降低了年度总使用量的单价,这通常是相当大的一笔节约。为了简化折扣问题的计算,计算有折扣时较大批量的库存投资这一步时往往可以忽略折扣的价值,即不妨以例中的¥2000代替¥1980。这样计算实际上不会显著地影响计算的结果。最小总成本法平方根EOQ公式根据成本与每一特定公式中所选定的其它因素为每种物品计算一个批量。然而它并未考虑这些物品在物料清单中的关系。一个装配件A(EOQ=200)可能是由组件B(EOQ=450)、C(EOQ=675)与D(EOQ=940)装配而成的。显然一个物品的EOQ同它在父物品中的使用方法之间应该有一种平衡关系;否则就会制造出并在库存中持有一些永远也用不上的组件(叫做剩余物)。平方根公式假设均匀的使用;实际上在成批制造中所有组件的使用都是不均匀的,它们是“成块地”发生的,等于其父件的批量,有时在同一时间期内同时供若干种父件使用。物品成本=¥4.00持有成本=30%/年=0.6%/周───────────────────────────────────未来净 第几周 累计 多余 持有 持有成本(¥) 订货 总成本需求 需要 批量 库存 周数 本批 累计 成本(¥)(¥)───────────────────────────────────93 4 93 0 0 0 0 30.00 30.00233 5 326 233 1 5.59 5.59 30.00 35.59194 6 520 194 2 9.31 14.90 30.00 44.90219 7 739* 219 3 15.77 30.67 30.00 60.6787 8448 9───────────────────────────────────*推荐的批量───────────────────────────────────图3-14 最小总成本法计算机化的MRP(见第6章)为每一物品推算未来的分时段的需求使它们可使用于批量决策之中以减少或取消剩余物以及假设均匀需求的必要性。最小总成本法就是这样一种技法。其基本假设同平方根公式是一样的:当持有成本等于订货成本时总成本将为最小。但它不假设均匀地使用,而使用未来的需求量,如图3-14所示。此法的机制包含一系列的反复计算。如果批量设定为93,等于第4周的需要量,故没有多余库存(它将在第4周内使用掉),并需要作一次生产调整。要满足未来的需求将需作另一次生产调整。如果第4第5两周的需求量一道做,批量将为326;因而将有233件要在库存中持有一个星期,但其持有成本(¥5.59)比再作一次生产调整要少得多。因此,这是一个较好的决策。逐次增加一周的需求量,批量与累计持有成本也将随之增大。当批量增大到739件时,累计持有成本为¥30.67,它非常接近于生产调整成本(¥30)。再进一步增大批量将使累计持有成本超过生产调整成本,不如再作一次生产调整去满足第8周及以后的需求。最小总成本指一个长时间期──譬如说几周──而不是指任何一个期间的总成本。本例中推荐的批量是739件。零件─期间平衡法这就是最小总成本法的别名与另一套计算方法,方法上基本是一样的。 这一变体是为IBM的软件包开发的,它更加便于编程序。零件──期间这一名词指1件物品持有1个期间,通常1个期间就是1周。如果将1件物品持有20周将相当于将20件物品持有1周。图3-15说明其计算机制,所用数据与图3-14中相同。订货成本 ¥30经济零件──期间=─────────────=──────=1,250单位零件──期间的持有成本 ¥4×0.006───────────────────────────────────未来净需求 第几周需要 累计批量 多余库存 持有周数 零件──期间数本批 累计──────────────────────────────────93 4 93 0 0 0 0233 5 326 233 1 233 233194 6 520 194 2 388 621219 7 739* 219 3 657 1,278───────────────────────────────────*推荐的批量───────────────────────────────────图3-15 零件──期间平衡法第一步是使用图3-15顶上的公式去算出经济零件──期间。然后逐步加大批量去满足相继而来的更多期间的需要并确定累计零件──期间,如此反复地计算如同在最小总成本法中一样。批量达到739件时,累计零件──期间为1,278,它就接近于前面计算出的经济零件──期间1,250,于是739件就是此法要推荐的订货量。注意最小总成本法与零件──期间平衡法给出的答案是一样的。瞻前/顾后为了精益求精,IBM给零件──期间平衡法增添了两个特色──叫做瞻前与───────────────────────────────────未来净需求 第几周需要 累计批量 多余库存 持有周数 零件──期间数本批 累计───────────────────────────────────219 7 739 219 3 657 1,278第1方案87 8 87 0 0 0 0448 9 535 448 1 448第2方案87 8 826* 87 4 348448 9 448 0 0 0───────────────────────────────────*推荐的批量大小───────────────────────────────────图3-16 瞻前特色顾后。在用零件──期间平衡法得出一推荐的批量,譬如说在图3-15的例中得出739件之后,程序进一步调查另一方案:看看下一期间(例中的第8周)的需求应不应被包括进刚刚算得的批量之中。注意第9周的大需求量448。第1方案不包括第8周,它将从第8周的需求87开始计算下一批,随后加上第9周的需求448,使得累计的零件──期间数达到448,如图3-16所示。第2方案则把第8周较小的需求87包括在本批之中,使原来推荐的739加上87变成826。然后,下一批将从第9周的448开始。这两个方案比较之下,程序将选用第2方案,因为它只涉及348个零件──期间,而第1方案要有448个零件──期间。特别注意这样计算所得的批量有了显著的变化;想想它对组件可得性与工作中心的负荷可能产生的影响。顾后特色是又一个改善订货的经济性的企图,如图3-17所示。在第1方案──────────────────────────────────
未来净需求 第几周需要 累计批量 多余库存 持有周数 零件──期间数 本批 累计──────────────────────────────────第1方案448 9 448 0 0 0 0153 10 601 153 1 153 15376 11 677 76 2 152 305226 12 903 226 3 678 98387 13 990 87 4 348 1,331175 1498 15第2方案448 9 448 0 0 0 0153 10 601 153 1 153 15376 11 677 76 2 152 305226 12 226 0 0 0 087 13 313 87 1 87 87──────────────────────────────────图3-17 顾后特色中,按照零件──期间平衡法的正常顺序,该技法确定出从第9周到第13周的最好的批量将是990件。然后首先向前考查第14、15周,结果未发现有显著好处。于是,它向后查看第9周到第13周的需求。由于第12周的需求远大于第13 周,图3-17中的第2方案显示出首先以677件做一批,再从第12周开始做下一批226件将比第1方案要好得多。它涉及的零件──期间比第1方案要少得多。所以推荐的批量将是677而不是990。注意瞻前与顾后二者开发出的订货量,变动非常大。这里是又一例子说明从用户观点看,一个好主意如何会被带到一种可笑的极端。最小单位成本法还有一个例子是最小单位成本法,它为反复计算的每一步计算一个单位成本。图3-18使用最小总成本法中讨论过的例子中同样的数据,第4列的总成本在反┏━━━━━━━━━┳━━━━┳━━━┳━━━━┳━━━━┓┃ 持 有 成 本 ┃订货 ┃ 总 ┃累 计 ┃ 单 位 ┃┣━━━━┳━━━━┫ ┃ ┃ ┃ ┃┃ 本 批 ┃ 累 计 ┃成本(¥)┃成 本┃批 量 ┃ 成 本 ┃┣━━━━╋━━━━╋━━━━╋━━━╋━━━━╋━━━━┫┃ 0 ┃ 0 ┃ 30.00 ┃ 30.00┃ 93 ┃ 0.323 ┃┣━━━━╋━━━━╋━━━━╋━━━╋━━━━╋━━━━┫┃ 5.59 ┃ 5.59 ┃ 30.00 ┃ 35.59┃ 326 ┃ 0.109 ┃┣━━━━╋━━━━╋━━━━╋━━━╋━━━━╋━━━━┫┃ 9.31 ┃ 14.90 ┃ 30.00 ┃ 44.90┃ 520 ┃ 0.086 ┃┣━━━━╋━━━━╋━━━━╋━━━╋━━━━╋━━━━┫┃ 15.77 ┃ 30.67 ┃ 30.00 ┃ 60.67┃ 739 ┃ 0.082 ┃┣━━━━╋━━━━╋━━━━╋━━━╋━━━━╋━━━━┫┃ 8.26 ┃ 38.93 ┃ 30.00 ┃ 68.93┃ 826 ┃ 0.084 ┃┗━━━━┻━━━━┻━━━━┻━━━┻━━━━┻━━━━┛图3-18 最小单位成本法复计算的每一步中都除以累计批量从而得出单位成本。这名字不大好。通常所说单
位成本是该物品每单位的物料、劳务与间接费用的总和;但在这里是指每单位物品的持有成本加上订货成本。在图3-18的例中,此技法的结论同最小总成本法与零件──期间平衡法所推荐的一样,都是739件。IBM与其它公司所做的若干次大规模仿真表明:最小单位成本法有时会推荐出不同的批量,而且──更为重要的是──不如其它方法经济的结果。1968年,有人在 APICS 季刊《 Production & InventoryManagement》上著文论“动态订货论”, 文中比较了最小单位成本法与最小总成本法并作出结论说,最小单位成本法的方法是不稳定的,用一组数据它会开发出较低的生产调整成本与较高的库存成本,而对另一组数据它会开发出较高的生产调整成本与较低的库存成本来,但不能保证使总成本最低。所以没有理由去使用最小单位成本法;为什么要多作些计算而去得到更差的结果呢?期间订货量(POQ)对于分时段的数据这是最简单的一种技法, 它把订货量表达为等于在若干个时间期间内(譬如六个星期内)的未来净需求的总量。根据订货成本与库存持有成本相平衡的原理,所用的时间期间应使期间订货量是“经济的”。最简单的方法是用平方根公式去算出EOQ,然后根据平均使用率把它转换成等效的供应时间期间,叫做期间订货量(Period Order Quantity)POQ。例如:EOQPOQ=─────────平均周使用量若 年使用量=15,600件该物品的EOQ = 2,100件2,100则 POQ =────────────=7周(15,600÷50)注意用的是近似计算,一年除50周得出平均周使用量,求POQ时用四舍五入得出最接近的整数的周数。这种计算无必要求其精确。现有库存=0 安全存货=0 提前期=2周──────────────────────────────────第几周 1 2 3 4 5 6 7 8 9 10 11──────────────────────────────────毛需求 510 115 320 400 270 190 605 360 180 410 335──────────────────────────────────未了结订货 925──────────────────────────────────净需求 20 400 270 190 605 360 180 410 335──────────────────────────────────应交订货 2025 1960──────────────────────────────────订货开始 2025 1960──────────────────────────────────图3-19 期间订货量图3-19所示为MRP程序中POQ的计算。图中对此组件的毛需求来自制造其父物品的已计划订单。本周到期的未了结订货为925(可能是一部份已完成订货的余额),它可以负担下2周的全部需求以及第3周的部份需求。根据刚刚算出的POQ为7周,故此技法将求出7周的净需求为(510+115+320-925+400+270+190+605+360+180)=2025。这一期间订货量应在第3周交货,其订单应提前2周在本周发出。下一个期间订单应在第10周交货,数量要小些(1960),但该订单要在第8周发出。此技法有一些优点。它以一定间隔定期地订货,有助于平滑对起始工作中心的输入。它满足推测的需求,不应剩下用不着的批量库存的剩余物。在图3-19的例中,倘若用了2,100这个EOQ,则第9周将产生余额75,这一数量不足以负担第10周的需求,因而仍必须另外订货。当然,需求中的变化将改变这种配合;如在第3周,未了结订货比满足该周需求所需的数量就缺了20件。另一种可能性当然可能是因为订货中有20件报废了。批对批理想批量的一个定义是它刚好等于今天或本周实际需要的数量。这种使订货量符合计划期间(通常为1周)的需求量的技法叫做批对批。这在MRP中很容易安排。这种安排使持有的库存很小,进入与通过各工作中心的工作流比较平滑并且更加可靠。物料搬运成本可能大。除非生产调整时间能被缩短,否则生产调整成本也将是高的。前面讲过的原理7强调短生产调整时间的必要性。实际的考虑还有一些确定EOQ的其它技法,其中包括 Wagner──Whitin 算法。由于它们很少实际应用,本书不再赘述。在数学家的语言中,这些形形色色的EOQ公式都是非常简单的模型。重要的是懂得EOQ的基本概念,而且能够确信所用的模型对所研究的特殊情况是最有效的。EOQ公式中包含许多假设,实际工作者要恰 当地来应用公式就必须懂得这些假设的意义。譬如说,这些公式假设,库存的持有量是发出这些订单的结果而且该库存将以相当均匀的使用率被提取。他们进一步假设在最经济批量的计算中,公式中所包括的因素就是唯一的起显著作用的因素,并且同订货与持有库存有关的成本均匀连续地随订货批量的大小而变。其它成本与有关因素在第二册讨论。本节的其余部份将讨论在应用EOQ公式时必须运用常识判断的几种实际情况。许多产品具有季节性的销售模式。常常可以看到大多数预期的产品需求在高峰季节到来之前老早就已生产出来,以保持全年的生产可以相当地平稳。在建立库存的这一期间,增加的那部份库存叫做预期库存,它不是批量库存,所以常规的EOQ模型是不适用的。这时公司不是要平衡订货成本与库存,而是试图以最经济的方式把工时储备在库存里。如果该季节性高峰非常短促,──例如圣诞节──库存经理唯一可凭借的实际信息就是销售预测,因为关于实际销售情况的信息返回时他已来不及作出反应了。因此,许多季节性产品全年就生产一批。下一批要生产什么的问题是通过比较各产品的劳务成本与物料成本,然后排序,使得劳务成本与物料成本之比最高的产品,能够在销售季节到来之前最早地生产出来,因而它们要在库存
中持有的时间也最长。对于季节性需求不太明显的大类产品,预期库存只存在一年中很短一段期间,将可以应用 经济批量的概念──但在建立库存的期间,有些批可以合并起来以减少生产调整。另一种常遇的情况是为装配件及其组件确定批量的问题。还是以极端情况为例最容易说明。对于由并不使用于其它装配件的专用组件构成的装配件,计算批量时应考虑组件与装配件的所有生产调整成本,而且大多数组件的制造批量应该同装配件一样。有些生产调整成本特别高的组件可以装配件批量的倍数来制造;简单地计算一下由此产生的库存与所节省的生产调整的对比,就可看出决策的经济与否。在大多数EOQ公式中没有考虑实际上对于不同的物品其占用空间的成本是可能大不相同的。装运用的纸板箱通常单价低,有非常吸引人的折扣并且要用大量的存储空间。另一方面,电子组件单价很高,而且用不着多大的存储空间。对这两种物品采用同一持有成本(假设存储成本包含在持有成本之中)将使后者支付的存储费多于前者。特别是对笨大的物品,估计一下EOQ计算结果需多大总空间是重要的;然后就可对相似的成组物品计算存储成本以得到实用的结果。记录上指示的订货量与工厂里实际使用的订货量往往是很不相同的。例如,在一个时常发生组件供应不足的装配车间里,可以发放出数量为2000到3000件的装配工作令,然而装配线上由于缺乏足够的组件供应,从来也做不到500或600件以上。将新的批量同现行订货量作任何比较以确定改变的效果与节约时,应根据在车间里实际上正在加工着的批量,而不是根据物料控制部门规定的数量。许多物品是通过一系列按顺序的作业加工的。这时的订货成本必须包括所有这些作业的生产调整成本的总和。如果其中有一个上游作业其生产调整占了总调整成本中极大的一部份,则在此高调整成本作业之后建立一种叫做持有点的库存然后再去以较小批量做进一步的加工可能是经济的。决定设置这个持有点应根据:是把该批加工到底从而生成已完工零件的库存;还是把该库存作为半成零件持有,然后再以较便宜的形式返回加工顺序。对这类计算要注意下列各点:1、选择究竟以半成品方式持有一物品的库存还是把它加工成完工零件时,在计算中应该只考虑实际受影响的那部份单位成本。把一个物品作为完工零件而非半成状态持有时, 库存投资中实际上只增加了半成点以后各作业的劳务与物料成本 (当然还有很少或可以不计的管理费),虽然会计记录难得承认这一点。2、补充已完工物品库存所需提前时间将被压缩而且在这个更加昂贵的阶段往往可以少持有一些库存。特别是当若干种完工物品可由一种半成品制成时,它的利益更大。这发生在,譬如说,当该半成品尚未涂色而可以涂成四种不同颜色之一去做成四种不同完工物品时。然而要注意,由于加工的批量更大,把该库存移动进出该持有点的时间也将增加,所以总的提前时间也可能增大。 3、一般地说,不应仅仅根据生产调整中的差异就去建立半成品持有点。半成品库存极难控制而且经过主要工序来加工极大的批量,往往使得为满足变化着的成品需求而作的组合控制十分困难。特别当生意正在增长而成品的需求不能完全靠持有点来满足之时,事情就是这样。从该持有点增长着的提货将产生大量补货订单,它们很可能──因为对这些组件,批量通常是大的──在主要工序处造成瓶颈,很快造成严重的缺货,因为不可能使每样东西都通过一些。4、持有点库存将要求更大的控制努力,更多的记录保管工作与更多文书工作。考虑建立持有点时对其优缺点应认识清楚。5、最好的周到解是去压缩生产调整时间。原理8.EOQ计算只是起点;修改它们以获取实际的结果。核查计算所得的EOQ是否合理的最好方法之一是请熟悉所涉及的实际情况的人们去作详细的评审。EOQ计算出来之后,熟悉制造设备的某人应同将应用该批量的工区的负责主管人员或同工作在该机器上的生产调整工一道审查它们,并把计算所得的EOQ四舍五入成为可使用的数字。由于EOQ曲线的扁平性,合理的四舍五入不会使EOQ的经济性受到多大损害。而这种评审将确保不致忽视应用该批量中的实际限制。有经验的实际工作者将核对每一EOQ的应用以确信该模型是有效的。彻底了解EOQ公式及其应用时,该技法可被用来收取巨大效益。但若此技法凭死记硬背盲目应用,其结果可能使公司实际上增加了成本。修改EOQ计算结果有许多理由。报废损失可通过把平均期望损失的百分数打进批量而获得补偿。可以在计算所得的EOQ下面设一条最小数量的底线以反映一供应商的最低采购量或每单位(块、张或筐)原料的最低制造批量。计算笨大物品时,由于存在空间限制可设置一个最大量作为上限。计算所得的EOQ还要调整到包装批(如打、货盘或圆桶等等)、搬运时的容器批或制造时的原料单位(成卷、成捆、成桶等等)的倍数。EOQ的计算可由于能产生确实的利益而是值得花费时间的,但也可以成为实际问题的根源。数学计算发出高度精确的辉光,但不要把它同准确混淆起来。不同的技法会给出不同的答案而试图花费时间去寻找“最好的”答案不过是一种琐事锻炼,不如把这份精力用在其它地方。频繁地重新计算EOQ会在计划系统中引起讨厌的精神紧张,第二册将充分讨论这个问题。这些公式一次解决一个物品;它对能力、总投资与系列产品关系的影响通常远大于个别物品上的节约 爱华网
爱华网