李萌 陈柳钦
(南开大学经济学院,天津,300071)(天津社会科学院,天津,300191)
[内容摘要] :本文采用上市公司未按时偿还贷款的比率(即贷款不良率)作为衡量信用风险高低的标准,结合独立样本t检验和主成份分析法,构造基于BP神经网络技术的商业银行信用风险识别模型。实证分析结果表明,单隐层BP神经网络模型对商业银行信用风险具有很强的识别能力,可以达到记忆能力和泛化能力兼容的最佳水平,但模型预测和推广能力还有待改善,所以在最终判定企业信用风险时必须结合其他定量和定性分析方法。本文研究结论也证明了单隐层模型要比双隐层模型优越,证实了双隐层无助于提高预测准确率的Lippm定理在中国的成立。
[关键词]:信用风险;主成份分析;BP神经网络;单隐层
Empirical Analysis of Credit Risk for Commercial Bank Based on BP Neural Network
Li meng Chen Liuqin
(College of Economics, Nankai University,Tianjin,300071)(Tianjin Academy of Social Science , Tianjin, 300191)
Abstract: This paper uses non-performed loan rate to measure credit risk of commercial bank,and tries to construct the credit risk model for commercial bank through BP artificial neural network. The empirically analytic results show the single hidden layer BP artificial neural network model does well in credit risk management and can reach the optimal level of combination of remember and enlargement ability while has improving room on prediction. So we should combine the model with other analysis method so as to get a precise result. It has been proved that BP neural network model with single hidden layer have more power than double hidden layer one, and prove well Lippm theorem which double hidden layer has no better use in improve prediction accuracy than single hidden layer can be found in China.
Key words: Credit Risk, Principle Component Analysis, BP Artificial Neural Network, Single Hidden Layer
一、导 言
商业银行信用风险的管理一直是国内外金融界关注的焦点问题。20世纪90年代以来,全球各金融机构不断推出新技术和新业务,商业银行大量使用金融衍生产品规避信用风险,这些新产品在提高银行风险管理水平的同时也对传统的信用风险度量技术提出了新的挑战。为了更准确地度量经营活动中的实际风险水平,大型国际商业银行纷纷推出内部信用风险模型;《新巴塞尔协议》第三次征求意见稿规定,除标准法外,银行可采用内部评级法度量信用风险,这意味着巴塞尔委员会对成员国的信用风险管理活动提出了更高的要求。从我国现状来看,目前商业银行尚不具备推行内部模型的条件,因此,结合我国信用风险管理的实际情况,构建过渡期间的信用风险识别模型,对控制和化解商业银行信用风险、提高我国银行业信用风险监管水平以及提升国际竞争力都有重大意义。
信用风险识别模型研究又可称为企业财务困境研究,二者本质相同,只是研究的出发点不同:从银行的角度看,叫做信用风险识别分析;从企业的角度看,叫做企业财务困境分析。早期关于财务报表信息与信用风险关系的研究主要以线性判别为主,在线性判别模型中又以Beaver(1966)的单变量模型和Altman(1968)的多元模型影响最为广泛。Libby(1975)首次将主成份分析方法引入判别模型以克服变量多重共线性的问题。由于神经网络技术在解决非线性建模问题上具有天然优势,许多学者尝试将其用于信用风险识别研究且大多得出了神经网络优于普通线性识别方法的结论。Odom和Sharda(1990)用BP神经网络预测了财务困境,结果显示神经网络模型优于判别分析模型。Altman等(1994)发现神经网络方法有时优于线性判别方法,但由于神经网络有时过度训练产生了不合理的权重,从总体上看线性判别方法要优于神经网络方法。Lee等(1996)以韩国公司的财务数据为样本比较了多层神经网络方法和多元判别方法(MDA),结果显示在财务困境预测问题上神经网络方法的预测效果和适应性均优于多元判别方法。我国对企业财务困境的研究刚刚起步,还集中于对企业财务困境的成因的定性分析和线性判别分析,如陈静(1999)首次在国内运用统计方法和计量模型进行财务困境预警研究。梁琪(2003)运用主成份分析与判别分析相结合的方法预测企业财务困境。王春峰等(1999)是国内较早采用神经网络模型预测企业信用风险状况的学者。总的说来,国内相关研究多是从上市公司角度进行的财务预警研究;且受数据来源所限(上市公司的履约情况和债项特征属于内部机密,一般研究人员很难获得),几乎所有研究都是以上市公司被宣布特别处理作为财务困境标志;构造模型时多基于线性判别技术,较少运用Logit模型和神经网络技术。
本文以上市公司未按时偿还贷款的比率(即贷款不良率)作为信用风险高低的衡量标准,结合主成分分析法和BP神经网络技术构造我国商业银行信用风险模型,采用我国某国有商业银行贷款客户的财务信息(主成份)和违约数据作为样本。BP神经网络实证分析的结论表明:单隐层BP神经网络模型对商业银行信用风险具有很强的识别能力,判定准确率可达100%,但模型的预测和推广能力较为有限,商业银行在识别、度量和预测信用风险时不能完全依赖于该模型。正文共分四部分,第一部分是导言,第二部分是BP神经网络模型构造,第三部分是实证分析,最后一部分是研究结论和政策启示。
二、BP神经网络模型构造
(一)主成份分析。为了避免包含企业信用风险信息的财务指标被排除在研究之外、最大限度地检验各种指标对企业信用风险的解释作用,此次检验将引入46个不同的财务指标。但指标的高维性特点又为研究带来了新的问题:这些指标之间高度相关,直接纳入分析不仅复杂,变量间难以取舍,而且可能因为多重共线性而无法得出正确结论。因此,在利用信用风险识别模型对我国商业银行的信用风险进行实证检验之前,我们首先引入主成份分析法。主成份分析法的基本思路是:从p个原始财务指标中提取m个相互独立主成份,每个主成份都是原来多个指标的线性组合。提取的主成份根据特征值大小排序,特征值最大的主成份对原始财务指标的解释力度最大,如果特征值小于1,表示该主成份的解释力度还不如直接引入一个原变量的解释力度大。如果m(m≤p)个主成份可以解释大部分原始财务指标的方差或者提取主成份的累计贡献率达到80%以上,那么m维主成份空间就能够最大限度地保留原始p维财务指标空间的信息。主成份分析的具体步骤如下:
1、原始数据标准化。设有n家上市公司样本,每个样本由p个财务指标x1,x2,……xp来描述,
…………(1)
其中Xi=(x1i,x2i,……xni),p为模型选取的财务指标的数量。由于主成份分析法的出发点是评价指标的协方差矩阵,而协方差容易受评价指标量纲和数量级的影响,因此,首先需要用Z-score公式将原始指标进行标准化处理,标准化后的指标矩阵为V,其中:
……………………………………(2)
其中,
2、计算相关系数矩阵(协方差矩阵)。标准化后,财务指标的协方差矩阵等于相关系数矩阵R(R=(rij)),rij的计算公式为,
……………………………………(3)
其中,
可以看出,R是实对称矩阵(即rij=rji),所以只需计算其上三角或下三角元素即可。
3、计算特征值和特征向量。通过雅可比(Jacobi)方法求解特征方程│λI-R│=0,得出特征值λi(i=1,2,…,p),因为R为正定矩阵,所以其特征值λi都为正数,按其大小排列,即λ1≥λ2≥……≥λi≥λp,特征值是各主成份的方差,它的大小反映了各个主成份在描述被评价对象上所起的作用。特征向量矩阵U可以通过方程│R-λI│U=0求得。
令F=UTV,也即 ……………………………………(4)
F被称为因子得分系数矩阵。
4、计算主成份贡献率和累计贡献率。第m个主成份Ym的方差贡献率为
前m个主成份Y1,Y2 ……,Ym,的累计方差贡献率为
Ym的方差贡献率am表示该主成份的方差在原始指标总方差中所占的比重,即第m个主成份提取得原始p个指标的信息量。因此,前m个主成份Y1,Y2 ……,Ym的累计方差贡献率a(m)越大,说明前m个主成份包含的信息越多。
5、选择主成份个数。如前所述,主成份分析的目的就在于将原来为数较多的指标转化成少数综合指标,同时尽可能多保留原始指标的信息,从而减少综合评价的工作量。因此,确定主成份个数要力图使k尽可能小而a(m)尽可能大,即以较小的主成份获取足够多的原始信息。确定主成份的个数,一般要求前m个主成份的累计方差贡献率不低于80%或者要求特征根大于1,本次研究将采用前者。
选取的m个主成份将矩阵U分成两部分:
则
其中 为主成份解释的信息, 为残余信息。根据因子得分系数矩阵,财务指标Vi可以表示为:
Vi=Ui1F1+Ui2F2+……+UimFm……………………(5)
二、BP神经网络模型构造
(一)主成份分析。为了避免包含企业信用风险信息的财务指标被排除在研究之外、最大限度地检验各种指标对企业信用风险的解释作用,此次检验将引入46个不同的财务指标。但指标的高维性特点又为研究带来了新的问题:这些指标之间高度相关,直接纳入分析不仅复杂,变量间难以取舍,而且可能因为多重共线性而无法得出正确结论。因此,在利用信用风险识别模型对我国商业银行的信用风险进行实证检验之前,我们首先引入主成份分析法。主成份分析法的基本思路是:从p个原始财务指标中提取m个相互独立主成份,每个主成份都是原来多个指标的线性组合。提取的主成份根据特征值大小排序,特征值最大的主成份对原始财务指标的解释力度最大,如果特征值小于1,表示该主成份的解释力度还不如直接引入一个原变量的解释力度大。如果m(m≤p)个主成份可以解释大部分原始财务指标的方差或者提取主成份的累计贡献率达到80%以上,那么m维主成份空间就能够最大限度地保留原始p维财务指标空间的信息。主成份分析的具体步骤如下:
1、原始数据标准化。设有n家上市公司样本,每个样本由p个财务指标x1,x2,……xp来描述,
…………(1)
其中Xi=(x1i,x2i,……xni),p为模型选取的财务指标的数量。由于主成份分析法的出发点是评价指标的协方差矩阵,而协方差容易受评价指标量纲和数量级的影响,因此,首先需要用Z-score公式将原始指标进行标准化处理,标准化后的指标矩阵为V,其中:
……………………………………(2)
其中,
2、计算相关系数矩阵(协方差矩阵)。标准化后,财务指标的协方差矩阵等于相关系数矩阵R(R=(rij)),rij的计算公式为,
……………………………………(3)
其中,
可以看出,R是实对称矩阵(即rij=rji),所以只需计算其上三角或下三角元素即可。
3、计算特征值和特征向量。通过雅可比(Jacobi)方法求解特征方程│λI-R│=0,得出特征值λi(i=1,2,…,p),因为R为正定矩阵,所以其特征值λi都为正数,按其大小排列,即λ1≥λ2≥……≥λi≥λp,特征值是各主成份的方差,它的大小反映了各个主成份在描述被评价对象上所起的作用。特征向量矩阵U可以通过方程│R-λI│U=0求得。
令F=UTV,也即……………………………………(4)
F被称为因子得分系数矩阵。
4、计算主成份贡献率和累计贡献率。第m个主成份Ym的方差贡献率为
前m个主成份Y1,Y2 ……,Ym,的累计方差贡献率为
Ym的方差贡献率am表示该主成份的方差在原始指标总方差中所占的比重,即第m个主成份提取得原始p个指标的信息量。因此,前m个主成份Y1,Y2 ……,Ym的累计方差贡献率a(m)越大,说明前m个主成份包含的信息越多。
5、选择主成份个数。如前所述,主成份分析的目的就在于将原来为数较多的指标转化成少数综合指标,同时尽可能多保留原始指标的信息,从而减少综合评价的工作量。因此,确定主成份个数要力图使k尽可能小而a(m)尽可能大,即以较小的主成份获取足够多的原始信息。确定主成份的个数,一般要求前m个主成份的累计方差贡献率不低于80%或者要求特征根大于1,本次研究将采用前者。
选取的m个主成份将矩阵U分成两部分:
则
其中为主成份解释的信息,为残余信息。根据因子得分系数矩阵,财务指标Vi可以表示为:
Vi=Ui1F1+Ui2F2+……+UimFm……………………(5)
(二)BP神经网络模型。人工神经网络是对生物神经网络系统的模拟,其信息处理功能是由网络单元的输入输出特性(激活特性)、网络的拓扑结构(神经元的联接方式)所决定的。人工神经网络是由大量的神经元互联组成,模拟大脑神经处理信息的方式并对信息进行并行处理和非线形转换的系统。通过样本信息对神经网络的训练,使其具有与大脑相类似的记忆、辨识能力。按照网络的拓扑结构和运行方式,神经网络可分为没有反馈的前向网络和相互结合性网络。前向网络由输入层,中间层(隐含层)和输出层组成,中间层还可有若干层,每层的神经元只接受前一层的输出。神经网络是近年来兴起的现代智能分析技术,作为研究复杂问题的有力工具,它能够很好地解决判别分析、Logit模型等传统分类方法不能解决的信用风险与财务指标之间关系非线性、财务指标呈厚尾分布等问题,在模型识别与分类、预测、自动控制等方面具有其他方法无法比拟的优越性。在信用风险识别研究中,最为常用的网络是BP神经网络、RBF神经网络和概率神经网络,BP网络是一种单向传播的多层前向网络,由于其良好的逼近非线性函数的映射能力和并行处理等特点,BP网络可以逼近任何非线性映射关系,从而求得问题的解答,而不是依靠对问题的先验知识和规则,适应性强,非常适合解决无规则、多约束条件或残缺数据的分类和模式识别问题。由于理论依据完善、又能够解决数据样本特征的限制极少,BP神经网络在解决分类问题时得到广泛青睐。本文将BP神经网络对我国商业银行的信用风险进行识别研究。
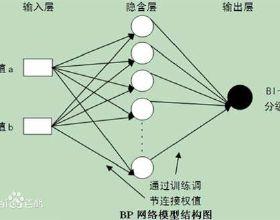
1、BP神经网络的基本原理。BP (Back Propagation)网络即误差逆传播神经网络,是能实现映射变换的前馈网络中最常用的一类网络,它是一种典型的误差修正方法,具有理论上能逼近任意非线性连续函数的能力,且结构简单,易于编程,在众多的领域得到了广泛的应用。BP网络是一种单向传播的多层前向网络,它解决了多层网络中隐含单元连接权的学习问题。BP神经网络可以看作是一个从输入到输出的高度非线性映射。在输入和输出层之间可以有一个或多个隐含层,信号是向前传递的,每一层节点的输出只影响下一层节点的输入,不带反馈和层内相互连接结构。当参数调整时,算法中含有误差反向传播过程(BP网络由此得名),通过反向传播学习算法,调整网络的连接权值,以使网络输出在最小均方差意义下,尽量向期望输出接近,反向学习的进程由正向传播和反向传播组成,在正向传播过程中,输出信息隐含神经元逐层处理并传向输出层,如果输出层不能得到期望的输出,则输入反向传播过程,将实际输出与期望输出之间的误差沿原来的连接通路返回,通过修改各层神经元的连接权值,使误差减小,然后转入正向传播过程,反复循环,直至误差小于给定的误差精度。BP 神经网络通常选用三层结构,即输入层、隐层和输出层,输入层与输出层的神经元个数完全根据分类问题的要求来设计,而中间隐层单元数的选择没有很好的解析式来表达,各神经元由网状结构连接而成(如图1所示)。
输入信号 输出信号
输入层 隐含层 输出层
图1 BP神经网络结构图
网络最基本的处理单位是神经元,其输出输入关系可描述为:
其中yj是从其他神经元传来的输入信号,θj为阈值,wij表示从神经元i到j的连接权值,f(l)为传递函数。传递函数有多种,例如S型(Sigmoid)函数、阈值型转换函数等。
2、BP网络参数确定和计算流程。设BP神经网络的各参数分别为:
输入层的输入:Ak=(y1,y2,……ym)
输出层的期望输出:Tk=(a1,a2,……aq)
输出层的实际输出:Zk=(z1,z2,……zq)
隐层的输入:Sk=(s1,s2,……sp)
隐层的输出:Bk=(b1,b2,……bp)
输出层的输入:Lk=(l1,l2,……lq)
隐层的阈值:θj(j=1,2,……,p)
输出层的阈值:γt(t=1,2,……,q)
输入层与隐层间的网络权值为wij,
隐层与输出层间的网络权值为vjt,
转换函数采用S型函数:
本次研究构造的BP神经网络信用风险识别模型将沿以下流程进行计算①:
1)权值和阈值初始化。随机给出权值|wij|、|vjt|和|θj|、|γt|的初始值,计算器归零。
2)给定输入信号Ak,(k=1,2,……,m)和期望输出信号Tk(k=1,2,……,q)。
3)计算神经网络前向传播信号。
隐节点的输入输出:
输出节点的输入输出:
实际输出节点和目标值之间的误差:
4)各层次权值和阈值的修正。如果误差不能满足误差精度要求,从输出层开始,误差信号将沿连接通路反向传播,以修正权值和阈值。
(a)权值的修正。分析误差与隐层和输出层之间权重的关系
(各输出节点之间相互独立)………………(6)
其中,
设
则
同样可以推导输入层与隐层之间的权重
………………………………………………………(7)
设
则
从以上推导过程可以看出,权值的修正量△wij、△vjt与误差函数梯度的下降成正比,因此可得:
,
,
ηη被称为学习率,综上所述,各层之间的连接权值修正公式为:
输出节点误差项: ………………………………………(8)
输出层权值修正:…………………………………(9)
隐节点误差项:…………………………………………(10)
隐层权值修正: …………………………………(11)
(b)阈值的修正。隐层和输出层阈值θj、γt也是变化值,在修正权值的同时也可对其进行修正,其修正原理与权值基本相同。
对于输出层阈值γt,
所以,输出层阈值修正公式为…………………(12)
对于隐层阈值θj,
其中,
所以,隐层阈值修正公式为,…………………(13)
5)随机抽取一个学习模式(样本)提供给网络,返回第3)步,直至n个模式(训练样本)全部训练完毕。
6)重新从n个模式中随机选取一个模式返回第3)步进行训练,直至训练误差达到误差精度(ε)要求,训练结束,即
。
①王伟:《人工神经网络原理——入门及其应用》[M],北京航空航天大学出版社,1995年版。
三、实证分析
(一)样本采集及数据处理。1、样本企业与财务指标的采集。此次研究的样本来源于在我国某商业银行2002、2003、2004年均有贷款且财务报表齐全的218家上市公司客户,3年共得到654个样本。在借鉴了国内外研究成果和穆迪、标准普尔等公司资信评级指标体系后,本次研究选取了46个财务指标(如表1所示)。数据来源于该商业银行信贷管理系统和证券之星(www.stockstar.com)、上海证券交易所(www.sse.com.cn)、深圳证券交易所(www.sse.org.cn)等权威证券网站。
表1 原始财务指标及其分类
由于种种原因,我国个别上市公司特别是财务状况不佳的公司的财务报表具有失真现象,陈小悦(1999)也发现上市公司为争取扩股权而普遍存在操纵利润现象,为避免类似情况可能对本次检验带来的负面影响,我们剔除了含异常指标的样本85个,所以正常样本就是569个。假设财务指标为xij(1≤i≤654,1≤j≤46),异常指标被定义为:。
2、样本数据的分组确定。样本被分为两组,2002年和2003年的样本为训练样本(390个),2004年的样本为预测样本(179个)。一般认为,国际上的优质商业银行不良贷款率在3%以下,中等商业银行在5%左右(王雍,2003),因此,本次研究以不良率5%作为高风险企业和低风险企业的分界线。根据以上分组标准,样本总体包括高风险企业191,低风险企业378个;在训练样本中,高风险企业148个,低风险企业242个;在预测样本中,高风险企业43个,低风险企业136个。
3、财务指标的独立样本t检验。由于本次研究引入的初始财务指标多达46个,为简化模型的检验过程,在实证分析前首先利用SPSS软件对全部财务指标进行独立样本t检验,检验结果表明,在两类企业之间有显著差异的财务指标共33个,分别为:营运资本、资产利润率、资产报酬率、息税前利润、净资产报酬率、平均股东权益、期末速冻资产、营运资本主营业务收入比、现金流量比率、利息保障倍数、总资产周转率、存货周转率、应收账款周转率、其他应收账款周转率、股东权益周转率、固定资产周转率、盈利增长指数、log(固定资产)、总资产增长率、留成利润比、留存利润总资产比、资产负债率、产权比率、留存收益、盈利波动率、资产短期负债率、净资产增长率、主营业务收入现金流量占比、筹资活动净流入现金与负债比率、每股现金流量、每股收益、每股净资产、股本账面市值比。
4、财务指标的主成份分析。SPSS等统计软件的默认设置都是以特征根大于1为标准抽取主成份的,经验表明,特征根标准确定的主成份数目偏低;而本次检验引入的原始财务指标较多,主成份提取不足很容易造成有效信息的丢失,因此,我们使用累计贡献率标准代替特征值标准。提取主成份时,我们还采用了方差最大化正交旋转法,正交旋转法并不影响主成份的提取过程和结果,只是改变了信息量在不同主成份上的分布,便于对主成份找到合理的经济解释。
基于主成份累计贡献率大于80%的标准,在对测试样本进行标准化处理后,模型从33个主成份中提取了12个。根据主成份负荷矩阵和因子得分系数矩阵,可了解各主成份与原始指标之间的相关关系,例如与主成份Y1相关关系最强的原始指标是净资产报酬率、资产报酬率、资产利润率、每股收益和留存利润总资产比,则可认定该主成份属于盈利性指标。
(二)实证分析过程。1、神经网络模型基本参数。本次研究中网络的训练和测试均通过Matlab软件完成,在用Matlab软件编制相应的网络训练和测试程序之前,首先要确定以下参数:1)网络类型。如前所述,笔者将基于单隐层的BP神经网络构建我国信用风险识别模型。2)各层神经元个数。网络的输入层引入主成份分析抽取的12个主成份,共12个节点,每个节点代表样本对应的主成份;输出层用一个节点表示,训练值为0表示低风险样本,训练值等于1为高风险样本。对于隐含层节点数的确定,在理论上并无明确规定,隐节点数太少,网络的记忆能力差,需要训练的次数多,训练精度不够;隐节点数太多,有利于对训练样本的拟合,但是过多的节点使得网络将输入生硬(rigidly)映射到输出,网络只是记忆数据而不是学习数据中的特征和尽力发现基本规则,对样本以外输入的响应就不是“柔性的”(soft),模型的泛化能力差。也即,BP网络用于模型分类时的记忆能力和泛化能力存在着矛盾:一方面需要充分的隐层和充足的节点存储复杂的类别边界信息,另一方面太复杂的结构会引来噪声,甚至使分类过程不能收敛。因此, 本文将采用生成结构法,从少到多,逐步增加隐节点数目,根据网络学习和训练的效果确定最佳的隐节点数目。3)误差精度。本文选用的网络误差精度为10-3。4)传递函数。本文构造的网络的输入层节点选用双曲正切S型函数,输出层采用线性函数。
2、单隐层BP网络模型的准确性和运行结果。将训练次数定为1000次,不同隐节点数对应的训练样本和测试样本的误判值如表2所示:
表2 单隐层BP网络模型的训练和预测结果
数据来源:Matlab输出结果。
图2 单隐层BP网络训练性能(隐节点=5)
图3 单隐层BP网络训练性能(隐节点=10)
图4 单隐层BP网络训练性能(隐节点=15)
根据模型的运行结果可知,随着隐节点的增加,单隐层BP神经网络模型的训练性能逐步提高(如图2至图4所示),总误判比率逐步降低;当隐节点等于10时,模型的总误判比率最低,只有11.42%,其中训练样本的误判率为0,测试样本的误判率为36.31%;隐节点超过10后,隐节点增加对提高模型判别的准确率无明显作用,总误判比率基本稳定在12%左右。在整个训练过程中,随着隐节点的增加,模型达到精度要求的运行步数逐渐减少,训练所能达到的精度逐步提高(隐节点等于1时,模型运行1000步只能达到0.1425的精度;而当隐节点等于20时,模型运行10步即能达到0.0003的精度),但模型的运行时间也有明显增加。
隐节点大于5的网络对训练样本判别的误判率都达到0,说明模型在训练过程中的自我学习和调整对提高判定准确性作用显著。隐节点等于10时,测试样本的误判比率达到波谷水平。说明BP神经网络模型最佳节点数是10,此时模型达到记忆能力和泛化能力兼容的最佳水平。但是,测试样本36.31%的误判率表明模型泛化能力还有待进一步改善。
3、双隐层BP网络模型的运行结果。为了进一步验证上述神经网络模型的性能,本文还采用双隐层模型与之进行比较。双隐层模型与单隐层模型的参数基本相似,只是传递函数有所不同。上述单隐层BP网络的输入层节点选用双曲正切S型函数,输出层采用线性函数;此次引入的双隐层模型在双曲正切S型函数和线性函数之间插入对数S型函数。误差精度仍定为10-3。双隐层BP神经网络的运行结果如表3所示:
表3 双隐层BP网络模型的训练和预测结果
数据来源:Matlab输出结果。
由表3看出,当隐节点等于10时,双隐层神经网络模型的总误判率最低,为11.95%,略高于单隐层模型11.42%的最低误判率,表明双隐层模型的判定性没有单隐层优越;而且对于其他隐节点数,双隐层模型的误判比率普遍高于单隐层模型。此外,相对于单隐层模型,双隐层模型的运行结果极不稳定,隐节点等于12和13时对训练样本的判定又出现错误。由于增加了一个隐层,双隐层模型的运行时间也明显高于单隐层模型。
尽管从理论上讲,增加网络的层数可以降低误差,提高精度,但从本次检验的结果可看出,双隐层模型并不比单隐层模型优越。Lippman R P(1987)等指出,在一定条件下,一个三层的BP网可以以任意精度逼近任意映射关系;且研究表明,与一个隐含层相比,用两个隐含层的网络训练并无助于提高小规模网络预测的准确率。本文进一步证实了该结论。
上述检验过程说明,可以通过构建BP神经网络模型企业的信用风险状况,单隐层BP神经网络的隐节点等于10时,判定的准确性最高,达到88.58%;其中训练样本准确率高达100%,测试样本的误判率为36.31%,该网络模型的推广能力还有待改善。相对于单隐层模型,双隐层网络无助于提高预测的准确率。
四、研究结论和政策启示
本文利用我国某商业银行218家上市公司贷款客户3年的财务信息和履约数据,构造了基于BP神经网络的我国商业银行信用风险识别模型并对其进行实证检验,研究的主要结论如下:
第一,基于BP神经网络技术构造的信用风险识别模型,既能够为商业银行识别和预测信用风险提供客观清晰的依据,同时也为借款人加强企业内部管理,摆脱财务困境提供有价值的参考信息。单隐层BP神经网络模型的最佳节点数是10,此时得到的输出结果如果是1,说明该企业是违约率高于5%的高风险企业,反之,如果是0,则说明该企业是违约率低于5%的低风险企业。
第二,单隐层BP神经网络模型对训练样本判定的准确率达到100%,这源于神经网络技术独特的自我学习和调整能力,对预测样本判定的准确率是63.69%,表明该模型的稳定性有待进一步加强,泛化能力有待提高。商业银行在具体运用该模型时,对企业信用风险的最终判定不宜完全信赖其判定结果,必须结合定性和其他定量方法(如Logit);另一方面,也意味着我国商业银行需要在实践中对BP神经网络进行技术调整以提高推广能力。
第三,相对于单隐层模型,双隐层网络无助于提高预测的准确率,单隐层网络模型要比双隐层模型优越。本文也证实了Lippman R P于1987年提出的定理在中国成立,即“与一个隐含层相比,用两个隐含层的网络训练并无助于提高小规模网络预测的准确率。”
第四,主成份分析可以有效解决我国企业财务数据高维性和多重共线性的特点,在不丢掉主要数据信息的前提下集中体现了他们的类别特色,使判别模型更具说服力。此次检验从46个财务指标抽取出12个主成份,主成份累计贡献率达到80%,在简化后续检验过程的同时最大限度保留了原始数据信息。根据旋转后的主成份负荷矩阵和因子得分系数矩阵中主成份和原始财务指标的相关关系,各主成份被赋予不同的经济意义。
参 考 文 献
[1] Altman, E., 1968, “Financial ratios, discriminant analysis and the prediction of corporate bankruptcy using capital market data”,Journal of Finance 4, 589-609.
[2] Altman, E., 1994, “Corporate distress diagnosis: Comparisons using linear discriminant analysis and neural networks (the Italian experience) ”, Journal of Banking & Finance, 1994,3.
[3] Odom, M.D., Sharda, R., 1990, “A neural network model for bankruptcy prediction”,Proceedings of the IEEE International Joint Conference on Neural Networks. San Diego, CA, 2, pp. 163-168.
[4] Beaver, W, 1966 , “Financial rations are predictors of failure”, Journal of Accounting Research, 4, Supplement, pp 71-111.
[5] Laitimen,E.K.,1993,“Financial Predictors for Different Phases of the Failure Process”,Omega,vol.21,No 2, 215-228
[6] Lippman,R.P.,1987,“Introduction to Computing with Neural Net”,IEEE ASSP,May,4,p4-22。
[7] 李志辉:《现代信用风险量化度量和管理研究》[M],北京,中国金融出版社,2001年版。
[8] 梁琪:《企业信用风险的主成份判别模型及其实证研究》[J],《财经研究》2003年第5期。
[9] 王春峰、万海晖、 张维:《基于神经网络技术的商业银行信用风险评估》[J],《系统工程理论与实践》1999年第9期。
[10]陈静:《上市公司财务恶化预测的实证分析》[J],《会计研究》1999年第4期。
[11] 杨军:《关于国有商业银行信用风险成因与识别的研究》[D],中国优秀博硕士学位论文全文数据库,2004年3月23日。
[12]李萌:《Logit模型在商业银行信用风险评估中的应用研究》[J],《管理科学》2005年第2期。
[13]李志辉、李萌:《我国商业银行信用风险识别模型及其实证研究》[J],《广东社会科学》2005年第2期。
[14]王春峰,万海晖,张维:《商业银行信用风险评估及其实证研究》[J],《管理工程学报》1998年第1期。
[15]张玲、陈收、张昕:《基于多元判别分析和神经网络技术的公司财务困境预警》[J],《系统工程》2005年第11期。
[16]方先明、熊鹏:《基于RBF网络的商业银行信用风险控制研究》[J],《金融论坛》2005年第4期。
[17]吴冲、吕静杰、潘启树、刘云焘:《基于模糊神经网络的商业银行信用风险评估模型研究》[J],《系统工程理论与实践》2004年第11期。
该文已经发表在《南京社会科学》2007年第1期上
 爱华网
爱华网