——基于渐近主成分分析方法
尹向飞 陈柳钦
(南开大学经济学院,天津,300071)(天津社会科学院,天津,300191)
[内容摘要]在文章的第一部分简单介绍了APT模型,并对APT以及APT实证分析中存在的一些不足进行简单地论述,然后介绍了渐近主成分分析法,在文章的第三部分对我国证券市场35只股票,运用渐近主成分分析法对单因子APT模型、五因子APT模型、十因子APT模型进行实证分析,并与CAPM以及他们相互之间进行比较研究
[关键词]APT;渐近主成分分析;拟合优度;公共因子
[中图分类号] F830.9 [文献标识码]A [文章编号]
一、文献综述
自从华尔街第一次革命——Markowitz投资组合理论问世以来,现代金融经济学获得飞速发展,诺贝尔奖获得者Markowitz的学生夏普在一般经济均衡的框架下,假定投资者都以均值-方差效应函数来进行投资决策,导出资本资产定价模型(简称CAPM)。自从夏普提出CAPM以来,CAPM被应用于各种投资决策,例如CAPM的被应用于度量各种风险证券或风险证券组合的系统风险。但是CAPM是一个单因子模型,并且还要求公共因子为有效的均衡市场组合的收益率,这一点无法检验。于是罗斯提出了一个多因素模型用来取代CAPM这个单因子模型对资产定价,这一模型称为套利定价理论(APT),其具体假设及结论如下:
假设有n种风险证券,风险证券i的收益率受到l个因素(或称为公共因子)的影响:
(1.1)
其中表示第j个公共因子的值,由于在一般APT模型中假定所有公共因子的均值为0,即各个公共因子是相互独立的,即,在我们这篇文章中,对于公共因子的均值为0不作要求;表示风险证券i对第j个公共因子的敏感程度,或者称为第j个公共因子对风险证券i的收益率贡献,为一系列随机“干扰”,其方差有限,即,其中,称为风险证券i的非系统风险,这一部分风险是风险证券所独有的,与其它证券无关,因此,在进行投资组合选择时,非系统风险是可以规避的,同时,随机“干扰”和公共因子相互独立,即。
当不存在渐近无套利机会时,那么对等式(1.1)两边求期望得到套利定价模型(APT)如下:
(1.2)
由于APT是一个多因子模型,其对因子的有效性没有要求,因此,在资产定价方面,APT被认为是一个比CAPM更好的替代模型。但是APT存在很大的不足,APT的多因素模型是以假设的形式引进的,那么公共因子的筛选存在很大的困难,这一困难体现在两个方面,第一方面,尽管假设任意一种风险证券的收益率受到多方面因素的影响,但是具体受那些因素影响我们无从考证,因此当我们选择一些因素作为风险证券收益率的公共因子作回归分析时,就有可能存在伪回归问题;一般地在套利定价理论实证分析方面的文章中,一般事先人为地选择国民生产总值、货币供应量、利率、通货膨胀率等一些宏观经济变量作为公共因子,但是实证分析的结果和实际以及一些经济理论不符。另一方面,即使我们知道哪些因素可能对某一风险证券存在影响,但是这些因素之间一般存在相关甚至共线关系,在用这些因素为自变量来解释风险证券收益率时有可能存在系数不稳定问题;当然,可以在这些因素中精选若干因素作为公共因子,但是这样处理存在两个问题,第一个问题精选的公共因子不一定能包括原来被选因素的绝大部分信息,第二个问题是公共因子的筛选工作量太大,例如假设有m个因素对风险证券的收益率存在影响,那么在精选过程中,一共有种可能,如果,那么就需要筛选1023次,在实践中,m往往大于10,那么计算量就更大。
针对因素筛选的问题,一般的解决办法是利用因子分析,因子分析是一类很好的降维方法,通过因子分析,可以将很多因素综合为少数几个公共因素,而且这些公共因素又包含原始因素的绝大部分信息,因此因素筛选的问题可以用因子分析法来进行解决;但是如何克服APT的多因素模型是以假设的形式引进的这一缺陷,这方面的研究文章较少。针对上面两个问题Connor 和Korajczyk(1986,1988)提出可以使用渐近主成分分析法(asymptotic principal components,简记为APC)来计算风险溢价。在假定方程(1.1)多风险因素定价关系的风险结构不变以及各种资产对风险的敏感程度在统计期内也不变的条件下,这种技术可以对大量的股票样本进行分析,在下一部分就APC进行简单介绍。
二、APC方法介绍以及步骤
为了方便起见,我们用矩阵形式来描述APT模型,(1.1)用矩阵形式来表示如下:
(1.3)
(1.3)式中为一个n维列向量,表示这n个风险资产在时刻t的收益,为一个l维列向量,表示这l个公共因子在时刻t的值,表示随机“干扰”向量在时刻t的值,。
第一步:计算,其中,为一个的矩阵,表示风险证券i在时刻j的收益率,表示一个n维列向量,为一个一个T维列向量,为无风险利率。
第二步:求的特征值,其中,其对应的特征向量为,以一定标准取前面l个向量为列向量组成一矩阵,一般情况下,以累计方差贡献率为标准。
第三步:以为被解释向量,以为公共因子矩阵,作回归(包含一个常数向量),计算残差,用以估计的对角线的元素。
第四步:计算,,重新估计特征向量矩阵,以及,以一定标准取前面l个向量为列向量组成一矩阵。
第五步:以为被解释向量,以为公共因子矩阵,重新作回归(包含一个常数向量),计算残差,用以估计的对角线的元素。
一般情况下,样本量是足够大,以致比没有太大的改进,因此在本文中,第四步以及第五步省略,由于,,因此第三步改为以为被解释向量,以为公共因子矩阵,作回归计算残差,用以估计的对角线的元素。从上面可以看出,利用Connor 和Korajczyk提出的渐近主成分分析法(APC)研究套利定价模型,存在以下优点:第一,无需事先选定因素,因此不存在多因素模型的先验性问题。第二,公共因子的数据是根据风险证券收益率的最原始数据直接通过渐近主成分分析方法加工得到,因此,风险证券和公共因子之间存在线性关系是有根据的,从而使得多因素模型在理论上更加具有牢固的理论基础。第三,公共因子的数据是根据风险证券收益率的最原始数据直接通过渐近主成分分析方法加工得到,它是对风险证券收益率的原始数据进行最佳综合和简化,保留了风险证券收益率的绝大部分原始信息,因此更加准确。第四,通过渐近主成分分析方法得到的公共因子之间不存在线性相关性,并且公共因子和残差之间也不存在相关性。
从以上可以看出,用APC方法来对APT进行实证研究比前些方法更为合理。
三、实证分析
我们从沪市选取江苏琼花、精工科技、科华生物、苏宁电器、七喜控股、武钢股份、马钢股份、广钢股份、宝钢股份、宁夏恒力、抚顺特钢、华夏银行、招商银行、民生银行、中信证券、空港股份、新黄浦、外高桥、招商地产、中粮地产、北京城建、陆家嘴、上海新梅、北京城乡、长江电力、涪陵电力等35只股票以及上证指数、深圳指数2005年8月15日至2007年8月13日的收盘复权价格(每只股票共463个数据,空缺数据用均值插补法补齐),这35只股票涉及中小板块8家,钢铁板块7家,金融板块4家,房地产板块9家,电力板块7家,选取股票的方式基本上为选取这五个板块的股票号码靠前的几只股票,当然每个板块都包含股本大的股票以及股本小或者相对小的股票。用表示第i种风险股票在时刻t的价格,表示第i种股票在时刻t的收益率,用表示市场证券在时刻t的价格,表示市场证券在时刻t的收益率,其中用沪市指数的收益率表示沪市市场证券的收益率,深市指数的收益率表示深市市场证券的收益率,无风险收益率为2005年4月发行的3年期国债的年利率(3.37%),收益率以百分之一为单位。构造一个指数,其收益率为这35种股票收益率的平均值,该指数在2005年8月15日的“价格”为100,实际上,这样的指数很容易构造,其价格为所有股票价格的几何平均值除以基期所有股票价格的几何平均值再乘以100即可,这种指数记为EW。
下面根据APC方法的步骤,我们来进行实证分析。
第一步,公共因子及其贡献率。由于收益率以百分之一为单位,并且样本数据较大,因此公共因子的特征值较大,第一个特征值竟达9981484.221,前面10个公共因子的特征值都大于20000,从第11个公共因子开始后面所有公共因子的特征值都小于20000。公共因子变量和他们的特征值的散点图见图1。
图1 特征值以及累积贡献图
从图1可以看出,前面5个公共因子的特征值变化比较明显,这5个公共因子的方差累计贡献率达到96.8%,也就是说这5个公共因子大约包含了原始数据96.8%的信息,因此用这5个公共因子作为APT多因素模型中的公共因子在一般情况下是可行的;如果对APT多因素模型的要求较高,前面10个公共因子基本上足够了,因为由前面10个公共因子构成的初始解中,他们的累计贡献率达98.4%;在所有的特征值中,第一个特征值的贡献率最大,它包含了原始数据的92.1%的信息,远远超出其他公共因子。
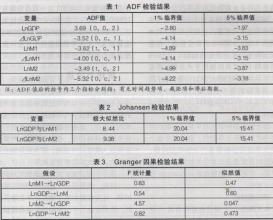
第二步,以上面35种股票以及EW为被解释变量(或因变量),分别对第一个公共因子和相应的市场证券收益率进行回归,得到的结果见表1(由于篇幅有限,因此只列出其中13只股票以及EW的回归结果)。在单因子APT模型(如果APT模型中只含一个公共因子,则称此模型为单因子APT模型,含五个公共因子,则称为五因子APT模型,依此类推)中,所有的股票以及EW的常数项a和ai1显著的不为0,所以在表1中没有表示出来。从表1,针对单因子APT模型,我们可以得出如下结论:(1)第一个公共因子对这35只股票以及EW存在显著的影响。从表1可以看出,所有的股票以及EW的系数ai1都显著的不为0,因此,第一个公共因子对这35只股票以及EW的收益率存在显著的影响。(2)在相同的板块内,第一个
表1 单因子APT模型以及CAPM的参数估价
注:在对CAPM进行参数估计时,由于每只股票的常系数参数的p值都大于0.1,因此在置信度为10%的条件下,不能拒绝零假设,因此令常系数项为0,重新进行参数估计,具体见表1。
公共因子对股本大的股票收益率的贡献基本上要小于对股本小的股票收益率的贡献;但是在不同的板块之间,不存在上述关系。例如,公共因子1个单位的变化,给涪陵电力的收益率带来0.7992个单位的变化,而仅给长江电力的收益率带来0.3897个单位的变化;公共因子值增加1个单位,给宁夏恒力、包钢股份、宝钢股份收益率带来的贡献分别为0.8741、0.6914、0.4893个单位,而他们的流通股股本安从小到大的顺序排列恰好为宁夏恒力、包钢股份、宝钢股份;当然也有例外,例如空港股份流通盘小于北京城建,增加1单位的公共因子对北京城建的贡献(0.8452)大于对空港股份的贡献(0.8092),但是相差不大,远远小于前面例子中的差异。中粮地产与精工科技属于不同的板块,尽管精工科技的股本小于中粮地产的股本,但是第一个公共因子对精工科技收益率的贡献小于对中粮地产收益率的贡献。(3)在所有股票的单因子APT模型回归方程的显著性检验中,F检验的显著性检验值p为0,这说明在置信度为5%的条件下,回归方程显著,即所有股票的收益率和第一个公共因子存在线性关系。(4)从拟合优度的角度来看,在相同的板块内,股本大的股票收益率的拟合优度要小于股本小的股票收益率的拟合优度;但是在不同的板块之间,不存在上述关系。例如,在单因子APT模型拟合中,涪陵电力的R2为0.5391,也就是说第一个公共因子解释了涪陵电力收益率53.91%的波动(方差),而长江电力的R2为0.2309,第一个公共因子解释了长江电力收益率23.09%的波动(方差);第一个公共因子对宁夏恒力、包钢股份、宝钢股份收益率波动的解释能力分别为45.54%、39.88%、33.43%,而他们的流通股股本按照从小到大的顺序排列恰好为宁夏恒力、包钢股份、宝钢股份;同样,第一个公共因子对精工科技、江苏琼花和苏宁电器的解释能力也说明这一点。这从侧面说明,小盘股票的股价容易操纵一些,而大盘股票的股价比较难操纵一些。(5)从拟合优度的角度来看,EW的R2为0.9967,也就是说第一个公共因子解释了EW收益率99.67%的波动(方差),远远高于对单只股票收益率波动的解释程度,因此用单因子APT模型对我国风险市场的股票进行套利定价是有效的。(6)除了EW以外,第一个公共因子对其他股票收益率波动的解释能力在13.53%至58.5%之间。
第三步,剩余公共因子解释能力的显著性检验。从表1可以看出,单因子APT模型解释了EW收益率的大部分波动,对其它股票的波动解释能力在13%至60%之间,那么就存在其它公共因子是否有必要加入APT模型成为公共因子的问题。为了解决这个问题,本文应用Wald检验对除第一公共因子以外的其它公共因子在APT模型中(五因子APT模型与十因子APT模型)的解释能力进行检验,具体结果见表2。
表2 剩余公共因子解释能力的显著性检验
注:aWald检验中的统计量在零假设下服从F分布,bp-value表示在零假设下获得一个更大统计量的概率。
从表2可以看出,在10%的置信度水平下,第二、三、四、五个公共因子对所有股票的解释能力显著,第六、七、八、九、十个公共因子除了对涪陵电力的解释能力不显著以外,对其它股票的解释能力显著。因此很有必要研究五因子APT模型以及十因子APT模型。
第四步,以上面35种股票以及EW为被解释变量(或因变量),分别对前面五个公共因子进行回归,得到的结果见表3(由于篇幅有限,因此只列出其中13只股票以及EW的回归结果)。在五因子APT模型中,所有的股票以及EW的常数项a和ai1显著的不为0,所以在表1中没有表示出来。
表3 五因子APT模型的参数估价
注:a五因子APT模型进行参数估计时,由于标记a参数的p值都大于0.1,因此在置信度为10%的条件下,不能拒绝零假设,因此此参数为0,重新进行参数估计,具体见表3。
从表3,我们可以得出如下结论:(1)所有股票(包括EW)第一个公共因子的系数都显著地不为0,并且都是正数,因此第一个公共因子对所有股票的收益率产生正的影响,如同沪深指数一样,第一个公共因子可以作为股票市场的总体趋势指标。(2)从总体来看,第二、三、四、五个公共因子对所有股票以及EW的收益率波动都具有很强的解释能力,但他们单独的解释能力都小于第一个公共因子的解释能力。(3)在相同的板块内,第二个公共因子对所有的股票收益率要么都产生正的影响或者都产生负的影响,第三、四个也同样如此(苏宁电器除外,因为尽管苏宁电器、精工科技和江苏琼花等同属于中小板,但是其流通股本达9.76亿,远远高于其他几只股票,同时从行业的角度看,苏宁电器属于零售业,和精工科技和江苏琼花等也不属于同一行业)。例如,第二个公共因子1个单位的变化,分别给宁夏恒力、包钢股份、宝钢股份的收益率的贡献率带来-3.4657、-1.4212和-0.4064个单位的变化,这说明股票的价格波动存在板块效应。(4)结合表1和表3,从拟合优度变化的角度来看(见表4),在其它相同的板块内,股本大的股票拟合优度的变化要大于对股本小的股票拟合优度的变化。例如,房地产板块中空港股份拟合优度的变化为0.144,即加入4个公共因子以后,APT模型空港股份收益率的波动解释能力从原来的49.35%提高到63.77%,提高了14.4个百分点,而对北京城建拟合优度的变化为0.1783,中粮地产拟合优度的变化为0.4223,而他们的流通股股本安从小到大的顺序排列恰好为空港股份、北京城建、中粮地产,这说明这四个公共因子的加入对大股本股票收益率的波动的解释能力的提高高于小股本股票收益率的波动的解释能力的提高。
表4 拟合优度的变化
第五步,CAPM和单因子APT模型、五因子APT模型的比较研究。(1)从CAPM的参数估价来看,这35种股票以及EW的常数项零假设检验时都不能拒绝零假设,而市场证券收益率的系数显著的不为零,其拟合优度在0.18至0.47左右,因此市场证券的波动对所有股票价格的波动存在显著的解释能力。(2)从表1可以看出,用CAPM拟合大盘股收益率的效果好于用单因子APT模型拟合同一只股票收益率的效果,而拟合小盘股收益率的效果恰好相反。例如,用CAPM拟合长江电力、宝钢股份、中信证券、招商银行时,他可以解释这些股票收益率的波动程度分别为27.05%、46. 6%、36.68%、43.1%,而用单因子APT模型拟合上述股票时,他可以解释这些股票收益率的波动程度分别为23.09%、33.43%、31.48%、24.47%;用APT去估计空港股份时,其收益率波动的解释能力为49.35%,高于用CAPM去估计空港股份收益率波动33.55%的解释能力,其它诸如北京城建、江苏琼花、精工科技也同样如此。造成这一结果的主要原因为沪深两市的指数是以一些主要股票尤其大盘蓝筹股的股价为基础加权而成,诸如精工科技、江苏琼花这些小盘股根本没有被选入股指,而且在构造这两个指数时,以被选入股指的股票的股本为权重,有些中小盘股即使选入,但是由于股本较小,对指数的作用效果有限,因此沪深两市的指数含有大盘股股价的信息远远高于其含有中小盘股股价的信息。(3)综合表1和表3,用五因子APT模型拟合所有股票收益率的效果好于用CAPM拟合相应股票收益率的效果。导致这一结果的主要原因为前5个公共因子大约包含了原始数据绝大多数信息。
第六步,拟合比较。比较两个或几个模型的优劣,有一种比较直观的办法,那就是首先制作一个覆盖所有股票样本的指数(在本文中应覆盖实证分析中所选的35种股票),然后求出指数的实际价格、各种模型的预测价格,把这些价格在同一张图上描述出来,然后做直观的比较,与实际价格曲线越接近的价格预测曲线对应的模型就越好,在本文中以EW为指数。(1)估计十因子APT模型的系数,具体见表5。
表5 十因子APT模型的系数估计
注:b十因子APT模型进行参数估计时,由于标记b参数的p值都大于0.1,因此在置信度为10%的条件下,不能拒绝零假设,因此此参数为0,重新进行参数估计,具体结果见表5第三行与第四行。
(2)原始价格的计算。,,其中表示EW在时刻t的价格,,表示EW在时刻t的实际收益率,其值为这35种股票收益率的平均值。(3)模型的预测价格的计算。,,其中表示EW在时刻t的预测价格,,表示EW在时刻t的预测收益率,其值是根据相应的模型求出的。
作图时,为了观察清楚,我们以3周为周期将EW的实际价格、各种模型的预测价格在同一张图上表示出来,具体见图2。从图2可以看出,在拟合EW指数时,应用单因子APT模型、五因子APT模型、十因子模型对原始价格进行预测时,误差很小;而应用CAPM来对原始价格进行预测时,在0到14以及23到25这两个时间区间,差误不大,但是在其它区间,误差较大,例如在15到23这一时间区间,运用CAPM预测出来的价格持续高于原始价格,在19这一点,预测价格高于原始价格约60,高出原始价格37.5个百分点;而在26到30这一时间区间,运用CAPM预测出来的价格持续低于原始价格,在28这一点,预测价格低于原始价格约50,低于原始价格12.5个百分点。因此,总体上,应用APT模型来预测股票的价格波动比CAPM效果更好。
图2 价格以及拟合比较图
注:ewp表示指数EW的实际价格曲线,f1fitp为单因子APT模型的预测价格曲线,f5fitp为五因子APT模型的预测价格曲线,f10fitp为十因子APT模型的预测价格曲线,f10-7fitp为十因子APT模型(除去第七个因子)的预测价格曲线
四、结论
从上述实证分析,我们可以得出如下结论:(1)不管从风险证券收益率的波动率还是从价格拟合效果来看,五因子APT模型以及十因子APT模型都好于CAPM模型。从总体上来看,单因子APT模型也优于CAPM模型。(2)从单因子APT模型对风险证券收益率波动的解释能力,我们推断出小盘股票价格较大盘股票价格更容易控制。(3)本文从各只股票的五因子APT模型第二、三、四个公共因子系数,发现股票价格的变化存在板块效应。(4)在APT模型的建立与求解中,利用渐近主成分分析法,可以提高模型的总体效果。(5)在相同的板块内,用多因素APT模型来度量大盘股收益率的波动优于小盘股收益的波动。
参考文献:
[1] Gregory Connor, Rober A.Korajczyk. Risk and return in an equilibrium APT: application of a new test methodology [J].Journal of Financial Economics,1988, 21:255-290.
[2] 张晓峒. 计量经济学分析(修订版)[M]. 北京:经济科学出版社,2006.
[3] Fama E, French K. Dividend yields and expected stock returns [J]. Journal of Financial Economics, 1988, 22:255-290.
[4] Roll R, Ross S. Economic forces and the stock market[J].Journal of Business,1986,59:383-403
[5] Lehmann B,Modestd. The empirical foundations of the arbitrage pricing theory[J].Journal of financial economics,1988,21:213-254.
[6] Fama E, French K. Multifactor explanations of asset pricing anomalies [J]. Journal of Finance, 1996,51:55~84.
[7] Fama, Eugene F. and James D. MacBeth. Risk return,and equilibrium: Empirical tests [J]. Journal of Political Economy, 1973,71:607-636.
[8] Jobson, J.D. A multivariate linear regression test for the arbitrage pricing theory[J]. Journal of finance, 1982, 37:1037-1042.
[10] Shanken, Jay. Multivariate tests of the zero-beta CAPM[J]. Journal of
Financial Economics, 1985,14,327-348.
[11] Shanken, Jay. Multi-beta CAPM or equilibrium APT:A reply[J]. Journal of Finance,1985,40:1189-1196.
[12] Ross, Stephen A. The arbitrage theory of capital asset pricing ,Journal of Economic Theory, 1976,13,341-360.
[13] Theil, Henri. Principles of econometrics[M]. Wiley, NewYork, NY, 1971.
[14] 张妍. 套利定价理论在中国上海股市的经验检验[J]. 世界经济,2000,10.
[15] 孙君敏,王频. 基于因子分析的套利定价模型及实证研究[J]. 财贸研究,2007,1:87-92.
[16] 余锦华,杨维权. 多元统计分析与应用[M]. 广州:中山大学出版社,2005.
[17] 马永开, 唐小我. 不允许卖空的多因素证券组合投资决策模型[J]. 系统工程理论与实践,2000,(2). [16]
[18] 东朝晖. 对套利定价理论及应用的认识[J]. 数量经济技术经济研究,2003,5:144-148.
The Demonstration Research of APT of our stock market:based on asymptotic principal components
Yin Xiangfei Chen Liu-qin
(School of economics- Nankai University,Tianjin,300071)(Tianjin Academy of Social Science , Tianjin, 300191)
Abstract: ATP and some shortages in APT and the demonstration research of APT are introduced in the first part of the paper. Then asymptotic principal components method is introduced. In the third part of the paper, based on asymptotic principal components method, we study the demonstration analysis of thirty five stocks in one –factor model, five-factor model, ten-factor model of APT and CAPM, and then comparative research is studied among them.
Key Word: APT; asymptotic principal components ; Goodness of fit; Common factor
该文拟在《金融管理科学—河南金融管理干部学院学报》2008年第1期刊发
 爱华网
爱华网