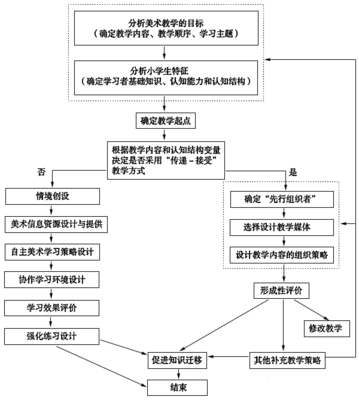
几何画板的精髓是:动态地保持了几何图形中内在的、恒定不变的几何关系及几何规律,是数学思想的直观体现,抽象问题的具体实验,现实情景的虚拟再现,瞬间事件的反复重现。它能按给定的数学规律和关系制作图形图象;还可进行实验来验证问题的真与假,从而发现恒定不变的几何规律,以及十分丰富的数学图像的内在美、对称美。几何画板化静态为动态,寓趣味性、技巧性和知识性于一体。几何画板还增大了信息的容量。它显示画面快捷、容量大、可储存,极大的提高了单位时间的利用率,为知识信息量的增大提供了空间。 几何画扳易操作的实用性,能让一个不懂电脑操作的教师或学生只需短暂地培训就可以上机操作,并且根据实际需求进行编辑和整理,有很强的实用性。 利用几何画板辅助教学关键的因素是选择适当的切入点。几何画板辅助教学的切入点,是指在实现课堂教学目标的过程中,最适合发挥几何画板优势的地方。实践证明:几何画板辅助教学的最佳切入点没找准将事倍功半,即造成浪费又达不到教学目标,有时还得返回传统的方式去重复教学内容,只有最佳切入点找得准,才会使课堂教学事半功倍,收到出奇制胜的效果,从而真正发挥辅助功能,达到优化教学的目的。[3]我从多年的几何画板辅助教学实践中,总结了一些最基本的切入点。 切入点一:在图形的变化和形成过程中使用 正确地教会学生识别几何图形,教懂学生作图,体会图形的变化和形成是突破几何教学难的切口。传统教学的局限性对学生认识图形、理解概念、建立图形与概念之间的本质联系等显得力不从心。数学教学,其实最难的不是学生学,而是教师教。这时用几何画板把图形的变化和形成动态化,方便于揭示图形的形成变化过程,使抽象的概念直观化、具体化,使学生能在灵活、丰富、规范的直观形象中理解抽象的知识,且很大程度上提高了学生的想象力和思维能力。 如用几何画板展示各种几何体的形成过程,能让学生很好的理解认识圆锥、圆柱、圆台、棱锥、棱台以及点、线、面、体的相互关系。 又如角平分线的性质与判定、线段垂直平分线的性质与判定等有关点的轨迹用几何画板制作动画,辅之以不同的线条颜色表示,可让学生非常直观地感受到轨迹的形成过程。 诸如此类运用几何画板适当切入优于传统教学的例子很多。在设计制作时,还可增加相关点、线条、面的闪烁以收起学生注意,还可用画面的迭加与分解来揭示某个知识形成的过程。 切入点二:在包含动态变化的知识中使用 心理学认为变动的事物、图形易引起人们的注意,从而在人脑里形成较深刻的映像。使用常规工具(如纸、笔、圆规和直尺等)画图,具有一定的局限性,并且画的图很容易掩盖极重要的几何原理。此时切入几何画板,制作出生动的动画,还可根据画图记录抽象出一个几何系统,当播放这个图形记录时,可以研究它各部分的关系和特殊情况,动态地观察、推测结论。 例1、在三角形高线的教学中,用几何画板制作动画:三角形形状在锐角三角形、直角三角形、钝角三角形之间变化,随之BC边上的高线也在三角形内部、边上、外部变化。另外还可通过三角形的各种图形变式,使学生能形象、直观地认识到各种三角形的高线与其它高线的本质区别。这样,只用一、二个动画,就方便快捷地克服了作钝角三角形高线这个难点。
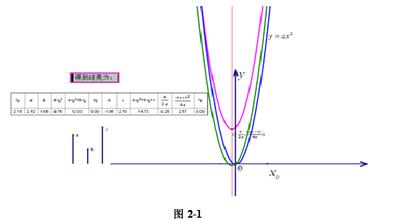
例2、在传授等腰三角形的“三线合一”时,用几何画板制作一个不等边三角形ABC,并用不同的颜色画出和标注过顶点A的中线AD、角平分线AE、高线AF,然后制作动画:当这个三角形的边AB逐渐和边AC相等时,E、F逐渐向中点D靠近,最终中线、角平分线、高线都重合在了一起。学生通过观察三条线段的变化过程,找出规律,发现定理,用此动画生动、具体地让学生体会了“等腰三角形的三线合一”这个概念。 例3、在中点四边形的形状变化此数学活动中,利用动画能生动地展现出由对角线不相等、不垂直的四边形逐渐变为对角线相等、对角线互相垂直的四边形时中点四边形的相应的形状变化。 学生对四边形ABCD的变化过程中四边形EFGH的特征能直观感受到,并且加深了印象。 例4、在四边形ABCD中,∠D=90°,BC∥AD,BC=20,DC=16,AD=30,动点P从点D出发,沿射线DA的方向以每秒2个单位长的速度运动,动点Q从点C出发,在线段CB上发每秒1个单位长的速度向点B运动,点P、Q分别从点D、C同时出发,当点Q运动到点B时,点P也随之停止运动,设运动时间为t(秒)(1)当t为何值时,以B、P、Q三点为顶点的三角形是等腰三角形;(2)是否存在时刻t,使得PQ⊥BD?若存在,求出t的值,若不存在,请说明理由。 这道题注重培养学生用动态的观点去看待问题。此时利用几何画板做出点P、Q的慢速运动动画,同时度量出线段QP、PB、QB的长度,引导学生仔细观察这三条线段的变化。并设疑:你认为这三条线段两两相等有几种情况?紧接着师生互动,合作交流得出是等腰三角形的几种情况。至于第(2)问学生之间相互合作作出图形,然后再加以分析,得出结论也就轻而易举了。这道综合题,通过运用几何画板的动画功能,使学生直观地观察到了图形的变化过程,使学生的数学抽象思维转化为形象的图形演示,让学生感悟到了动态几何的学习方法。 切入点三:从常量到变量时使用 静态的图形、图像使原本相互联系的知识割裂开来,失去了知识之间的内在联系,会使学生只注意事物的局部而忽视整体。几何画板能动态地展示问题的特点,可以克服静态图形的这一缺陷。[2] 在探索正比例函数y=kx的性质时,通过直线上点P运动时纵坐标y随横坐标x的变化过程,形象直观地展示了k值不同时图象的相应性质。 又如在讨论二次函数y=ax2+bx+c(a≠0)或y=a(x+h)2+k(a≠0)中,二次函数图象与常量a、b、c、h、k之间的关系时。可作以下设计: ①在演示画面中,实时显示抛物线的顶点坐标、与y轴的交点坐标和对称轴。②拖动有向线段a,改变a的取值。观察抛物线开口方向及大小。③拖动有向线段c,改变c的取值。观察可发现抛物线随c的值变大、变小而升高或降低。并可观察抛物线与y轴交点的纵坐标和c的取值相等,从而得到抛物线y=ax2+bx+c与y轴交于点(0,c)。④拖动有向线段h、k,改变h、k的取值。观察得抛物线随h、k的变化而左右平移或上下平移。顶点坐标是(h、k),也就是(,)。从而归纳出抛物线的顶点坐标与对称轴和h、k的关系,并将实验观察所得结论,进行推理论证。 这样,描述客观世界运动变化规律的数学模型——二次函数,以变化和对应为基础的这一重要数学概念。以往需要给学生提供大量的图象素材让学生观察、分析与对比,并靠老师口头讲解、黑板上画图都难达到要求。而通过几何画板动画,学生很轻松地就理解了二次函数的变量之间的相互依赖关系,清楚地看到二次函数的几种形式之间的平移、对称关系。 切入点四:在空间图形与平面图形互相转化时使用 几何画板能以动态图形展现奇妙的图形变换。逼真、细致的动画展示,使学生在领略数学的奇异美的同时,也学到了新的知识。它弥补了传统教学方式在直观感、立体感和动态感方面的不足,处理了传统教学方法难以处理的问题,激发了学生的兴趣,增强了直观印象。 通过平移、旋转、翻折等计算机演示的变换及学生动手操作实践,引导学生借助直观的、丰富的变化着的图形,找到证题的思路并扩大思维的空间想象能力,让学生既发展了空间观念,又获得了良好的体验。 例如,在教授圆锥的侧面展图时,学生通过剪出扇形,围成圆锥,又展开……这一手工实践操作,同进屏幕上辅以几何画板制作的动画,能让学生真切地体会到立体与平面的转化,进一步加深了学生的理解,巩固了展开后的扇形弧长即是原来圆锥底面圆的周长……,几何画板制作动画适时切入,无疑让原本就已生动的教学更是如虎添翼。 又如:在学习图形的三种变换平移、旋转、翻折的过程中,让学生动手实践操作的同时,辅以几何画板动画演示(有条件时,可在计算机教室让每位学生自己动手改变图形形状并演示动画),这样的学生参与,更加激发了学生的兴趣和激情,活跃了学生的思维,激发了他们求知的欲望。 切入点五:在探索规律性问题时使用 规律探索型问题:就是对材料信息的加工提炼和运用,从而得出数学概念和规律。 例如为探索函数y=kx+b与函数y=x图象之间的关系,可用几何画板制作动画,通过调整k、b的任意值,显示出相应的y=kx+b的图象,再由y=x的图象先绕原点旋转成为y=kx的图象(保持原有图象),然后再沿y轴的正方向(b>0)或负方向(b<0)平行移动|b|个单位,从而由重合使学生深刻感受到坐标系中的图形变换,并观察归纳出直线y=kx+b与与y=x的关系。y=ax2,y=ax2+k,y=ax2+bx+c,y=a(x+h)2+k的图象关系探索也可用此类动画来揭示规律。 切入点六:在图案设计和展示数学美时切入 几何画板辅助教学是教学艺术与计算机技术的加工和整合,它可以使用光、形、色等要素来表达教学内容中美的本源现象。奇妙的图形变换,使我们领略了数学的奇异美;各种图形的有机组合、逐步发展,展示了数学的和谐美;通过图形的旋转、翻折,表现了数学的对称美……,所有这些,充分说明了几何画板辅助教学,可使教材中那些富有诗情画意的美的因素得到足够的展示,学生定会从中感受到数学并非那么枯燥无味、深不可测,而是如此神奇美妙,瑰丽迷人。 当然,几何画板教学只是传统教学的一种辅助,一种补充,不可能完全替代传统教学。无论怎样,二者都不可废弃。所以我们应清楚地认识到二者各自的优劣,寻找二者最佳的结合点,以提高教学效率。 几何画板的应用要注意适度,要恰到好处。只有确实需要运用几何画板辅助教学的内容,才去选择它,但不一定整堂课都用,一堂课不能像走马灯似的,用得太多、太滥。毕竟,我们的主体是学习数学,而不是学信息技术,不能为了技术而技术,从而导致相反的效果。而应以实现数学目标为最根本的出发点,以改善学习者的学习为目的,合理恰当地使用几何画板。
 爱华网
爱华网