每到年初,各个国家都会公布其上一财政年度的国民经济核算报告。不过,由于经济学基础理论的问题,除了人造数据之外,非人造的数据同样缺乏科学性和可信性。
经济学人喜欢旁征博引,经常用科学的外衣来包裹其非科学的内容,例如曾经把毫不相干的欧拉定律拿来证明资本主义分配方式的合理性。现在本文也比葫芦画瓢,用电工学的基尔霍夫第一定律来告诉经济学人到底应该如何核算国民总收入等等宏观流。不过,这可不是用科学包裹伪科学,而是要籍此拆穿伪科学的面貌。
为展开此文,先介绍一下电子学上赫赫有名的的基尔霍夫定律(Kirchhoff’s laws)。此定律1845年由德国物理学家G.R.基尔霍夫提出,包括电流定律和电压定律,阐明集总参数电路中流入和流出节点的各电流间以及沿回路的各段电压间的约束关系。本文只谈对经济流核算有指导意义的基尔霍夫电流定律。
基尔霍夫电流定律(KCL):任一集总参数电路中的任一节点,在任一瞬间流出该节点的所有电流的代数和恒为零,即 ΣI=0
也有写为:ΣIin=ΣIout,即流入节点的电流之和恒等于流出节点的电流之和。
就参考方向而言,流出节点的电流在式中取正号,流入节点的电流取负号。由于针对“节点”而言,基尔霍夫电流定律又称“节点电流定律”,是电荷守恒定律在电工学应用中的体现,是电工学当中的一个重要的基本定律。
在基尔霍夫定律当中,电流的正负号问题十分重要,这意味着,基尔霍夫的“电流”既包含电流相对应“节点边界”的流入,也包含电流从“节点边界”的流出。
所谓“节点边界”。在电工学上,基尔霍夫的“节点”并不是一个无体积大小的空间“点”,而是一个有大小但不考虑其大小的“区域”。
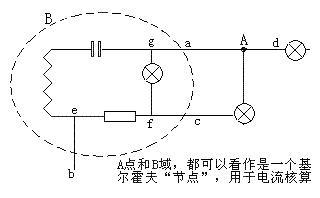
我们可以如下图所示在一个电路系统中任意画出一个包含若干电子元件和线路在内的“区域”如B,这也是一个“节点”,对这个区域的电流核算,同样适用基尔霍夫的节点电流定律。当对B域这个节点进行电流计算的时候,根据基尔霍夫定律,只需要考虑a、b、c三个出入口的电流就可以了,即把B当作A一样的实点看待,不需要再去考虑如e、f、g点这种内部节点的电流情况了。
基尔霍夫定律不仅告诉我们,对于任意一个节点来说,其外部流总和为零,同样告诉我们,节点内部流之和也为零。这当然是物质守恒定律处处适用的必然结果。
一个非孤立的经济体,也可以把它视为一个没有容积大小、有价值流或货币流进出的“节点”,就如同基尔霍夫节点电流定律可以把一个电器元件甚至一部分线路当作一个“点”看待一样。
如果我们把基尔霍夫电流定律用来经济体系中货币流的核算的话,显然我们习惯上可以接受的“参考方向”是,当货币流取正值时,是“收入”,货币流向“经济体节点”即“所有权域”;而当货币流为负值时,货币从所有权域中流出,意味着“支出”。这一点同基尔霍夫定律当中电流“流入为负,流出为正”恰恰相反。
如果用数学化的语言讲,就是说,收入、支出等等变量都是矢量,具有方向性,这个方向性就说针对所有权域而言的。矢量就不能简单地把数值部分加和,而要考虑其方向性决定的正负号。
根据基尔霍夫节点电流定律的原则,针对“家庭”的收入,只能是从“家庭”之外流入这个家庭的。我举两个例子。例如某名人不让自己的老婆到外边工作,但是给她开出非常可观的“工资”让她在家做家务。如果要考虑这个名人的“家庭收入”的话,她老婆做家务工作的工资,就不是这个家庭的收入项目之一,因为这属于“内部流”,是从丈夫自己的收入当中分给他老婆的,不能够把名人的收入和他老婆的收入加起来算做他家庭的总收入。
再例。如果不是把收入和支出混为一谈的话,把每个家庭成员的收入加起来当作家庭总收入,就会发现,这个“和”总是大于家庭的实际收入。为何?因为孩子说他做家务得到父母的奖赏也是他的收入,而这同时也是父母的支出。
这两例当中的错误,就在于没有认识到“内部流之和必为零”这个基尔霍夫结论。
(请续看下集)
 爱华网
爱华网



