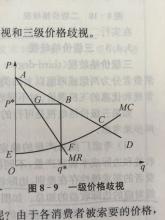
教科书上讲:垄断厂商没有供给曲线。
面对一条既定的需求曲线,垄断厂商只存在唯一的供给点,因而垄断厂商没有供给曲线。
但我们要问,垄断厂商是因为什么而没有供给曲线的呢?怎么竞争厂商有供给曲线而垄断厂商就没有供给曲线?如果垄断厂商没有供给曲线的话,寡头厂商有没有供给曲线?垄断竞争厂商又有没有供给曲线?如果垄断竞争厂商没有供给曲线的话,那么“剪刀模型”还有什么价值吗?该怎样理解“剪刀模型”的供给曲线和需求曲线呢?
教科书上所说的垄断厂商没有的供给曲线,是求解约束条件下的利润最大化问题而推得的供给曲线。这条供给曲线,需求曲线是重要的约束。给定一条需求曲线,只有唯一的供给点;需求曲线移动,才会产生一系列的供给点。对于竞争厂商而言,对应一条价格线(一个价格水平),存在唯一的最优供给量;价格线变化(价格水平变化),最优供给量跟着也变化。似乎竞争厂商存在供给曲线,而垄断厂商不存在供给曲线。但我们要明白,那条价格线不是别的,正是竞争厂商的需求曲线。这样看,对于一条既定的需求曲线,竞争厂商也只存在唯一的供给点——竞争厂商与垄断厂商并没有本质的分别,为什么我们要讲竞争性厂商存在供给曲线而垄断厂商不存在供给曲线呢?
假设厂商的需求函数为Q=Q(P),成本函数为C=C(Q)。则利润最大化的一阶条件为:
。
其中ε为需求价格弹性。这个等式就是利润最大化条件下价格和供给量要满足的关系。在需求曲线的约束下,这个等式决定了唯一的供给点(P,Q);需求曲线移动,供给点(P,Q)的轨迹就形成一条曲线——求解约束条件下的利润最大化问题而推得的供给曲线。如果ε→∞,也就是需求的价格弹性趋于无穷大,那么上述等式就变为P= 。这就是常说的竞争厂商的供给曲线了。
竞争情况无非是一般情况的极限状态。我们没有理由认为竞争厂商存在供给曲线而垄断厂商不存在供给曲线。如果用求解约束条件下的利润最大化问题来定义和推导厂商的供给曲线,那么任何厂商都是有供给曲线的。只不过这条供给曲线是一般均衡的产物,是可以呈任何形状的:不但可以向上倾斜,还可以向下倾斜,甚至可以绕着圈的行走,或者退化为一点;不仅是一般均衡的产物,可以呈任何形状,而且这条供给曲线还依赖于需求曲线。
在我们看来,罗宾逊夫人对于垄断的分析实在要好于张伯伦的分析。好在哪里呢?好就好在一般化。夫人的分析框架,于竞争厂商、垄断竞争厂商、寡头厂商、垄断厂商是没有分别的。事实上,无论那种厂商,都是追求利润最大化的。既是追求利润最大化的,那就遵循“边际收益等于边际成本”的等边际原则,所不同的只是它们面对的需求曲线的性状不一样,因而边际收益和边际成本的具体表现形式不一样罢了。
问题是:这样的通过求解约束条件下的利润最大化问题而推得的供给曲线是马歇尔“剪刀模型”的供给曲线吗?这样的供给曲线与“剪刀模型”的供给曲线有着怎样的关系呢?
答案是:此供给曲线非彼供给曲线!“剪刀模型”的供给曲线是局部均衡的产物。那里,“其它因素不变”是重要的约束;那里,供给曲线不依赖于、也不能依赖于需求曲线。而通过求解约束条件下的利润最大化问题而推得的供给曲线则是一般均衡的产物。这里,好多因素其实是变化的;这里,供给曲线依赖于需求曲线。“剪刀模型”的方法论特征,马歇尔本人讲得十分清楚,后人也知其方法论特征,但在运用的时候常常又忘记了这一方法论特征。
如果这条供给曲线是“剪刀模型”的供给曲线的话,那么“剪刀模型”就没有了实质的意义。如果“剪刀模型”的供给曲线不但可以向上倾斜,也可以向下倾斜,甚至可以绕着圈的行走,或者退化为一点,那么“剪刀模型”还有什么实质的意义呢?
我们曾经撰文,讲“剪刀模型”的需求曲线不同于通过求解约束条件下的效用最大化问题而推得的需求曲线;二者虽然不同,但并不矛盾,后者是沿前者的移动与前者本身的移动合成的移动。这里讲供给曲线,道理是一样的:不是说这两条供给曲线逻辑上有什么不一致的地方,而是说“剪刀模型”的供给曲线是局部均衡的产物,而通过求解约束条件下的利润最大化问题而推得的供给曲线则是一般均衡的产物。后者是沿前一条曲线的移动和前一条曲线本身的移动合成的移动,并且还是在需求曲线的约束下合成的移动。
可以这样讲,通过求解约束条件下的利润最大化问题而推得的供给曲线是马歇尔需求曲线和马歇尔供给曲线的交点移动的轨迹。我们要记住:一般均衡乃是局部均衡的“合成”,而局部均衡则是一般均衡的某种“分解”;二者既联系,又相区别。
最后的问题是:以马歇尔供给曲线而言,垄断厂商存在供给曲线吗?答案是:也存在。马歇尔本人就曾用供求框架对垄断进行过分析。当然,还是那句老话,我们不要忘记了马歇尔供给曲线的局部均衡特性。
 爱华网
爱华网