(续接上帖)
熵概念的错误更多是出在“热”这个概念之上,而论及这个问题又涉及到热力学的“温度”概念。由于热力学只考虑平衡态,故所考虑的温度不是一个正常的温度概念,也就是说,“热”是两个平衡态温度不同的物系之间的能量传递,而不是其中某个系统的性质,这样一来,说熵是态函数,就意味着一个系统的自身内部状态要依赖与一个外在系统的关系进行定义,这显然是荒谬的。
宇,空间;宙,时间。“往古来今谓之宙,四方上下谓之宇”(刘安《淮南子·齐俗》)。宇宙即随时间而拓展的空间,现在物理学的属于叫做“视界”。因此,谈论宇宙间万物变化的时候就有两个层次:一是随时间的变化,二是随空间的变化。如果是谈及一个时点上的状态量的变化,就是“宙”的问题,而谈及不同时段内的过程量变化,其实就是“宇”的问题了。这在物理学当中,就是所谓的“场”的概念:场者,随时间和空间的分布是也。几何学上意味着一个三维空间坐标系附加一个整体移动的时间维度。
所以,“温度”概念有一个在体系中的分布问题,即所谓的“温度场”,T=T(x,y,z,t),表示温度是基于空间位置和时间而变化的,这就是现实事物的温度场数学模型。如果逐点改变但不随时间改变,T=T(x,y,z),叫做稳定的温度场;如果物系内各点的温度在每一个时点上都保持相同,则叫做均匀的温度场,即T=T(t);如果既稳定又均匀,则称为稳定均匀的温度场,也就是物系内各点温度相等且保持为一个常数不变,既T=To。
由于热力学考虑的是平衡态,也就是说,它所考虑的“热”不是、也不可能是由于体系内部的温度场差异造成的热流,而只能是系统和外部环境(另一系统)之间的热流。热力学教科书也会提醒读者“具有内部热流和粒子流的体系不是平衡态”。这就决定了一个误入歧途的思路:以两个系统的关系来定义其中一个系统的性质。最终导致怪胎“熵”概念的产生。
虽则热力学考虑的物系状态都是指平衡态,然而我们应该注意到,平衡态只是均匀场而非稳定场。均匀温度场T=T(t)应该随时间变化,但大多情况下除考虑传热速度的时候之外,热力学中很少提及时间变量t。而即便是在讨论传热速度的时候,也很少让时间变量显现出来,少有dQ/dt这种表达。热传递最终都是以冷热源温度达到一致为对象的,也就是说t是足够大或无穷大——换句话说:把时间(速度)问题放在一边。
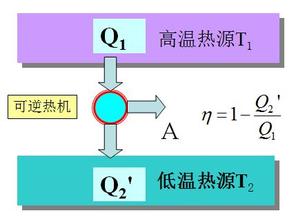
热力学为何要这么做?当藏匿了时间变量t之后,在熵的表达式中,T就变成了环境的温度(当然也是物系最终达到的温度),Q是环境和物系之间传递的热,如此一来,一个物系(介质)的态函数竟然是全部由外部物系和环境的参数所定义——高温热源的温度T1、低温的温度T2、热源传给介质的热Q1、介质传给冷源的热量Q2、介质对环境或者环境对介质所做的功——惟独看不到介质自身的性质参数,岂不令人奇而怪之?由此定义出来的态函数反映的究竟是谁的“态”?介质的?热源的?冷源的?环境的?还是总体的?
熵概念的错误之二:用物系间的关系定义一个物系的自身性质。
我们给出下面的实验,来进一步说明熵概念的问题重重。
在这个实验当中,两个物系从原来的分隔状态(一)到热接触状态,但是热接触的时间不是无限的,因此两个物系温度没有达到一致便被再次分开为隔离状态(二)。
http://s2.album.sina.com.cn/pic_3/5562bb43020014wp
热接触之前,A、B分别具有平衡态温度Ta1和Tb1,Ta1≠Tb1;热接触之后,A处于平衡态温度为Ta2,B处于平衡态温度为Tb2,Ta2≠Tb2。Ta2和Tb2既是A、B最终达到的平衡态温度,也看作是从热接触状态分开时的瞬间温度。问题:(1)在(一)和(二)中,A、B有各自的熵吗?存不存在整个物系(A+B)的“总熵”问题,如何计算?
(2)在热接触过程中的任意时刻,A物系、B物系各自的熵是多少?“A+B”物系的熵又是多少?如何计算?
显然,在(一)和(二)当中,A、B物系是各自独立的,不存在“热”,则作为“热温商”的熵也无从考虑。而在热接触当中,虽然因为温差存在(Ta1≠Tb1)有传热现象,但是没有达到最终A、B等温(Ta2≠Tb2),A和B互为环境而且是处于不稳定的变化当中,一个逐步降温一个逐步升温,所以,传统的、用不变的环境温度来计算熵的做法也无所适从了。
最关键的一点,不论在接触前、中、后,有没有“总熵”的问题存在。这个问题等同于“一个真正的孤立系统到底有没有熵?”。为此,我们把上面的实验扩大到无限多个物系A、B、C、D……,当总体积有限而物系数量足够大的时候,这实际上就是我们面对的现实——(一)和(二)是稳定场T=T(x,y,z),而热接触过程就是现实中的宇宙T=T(x,y,z,t),各个子物系相当于一个不考虑体积问题的质点。这就演变为考虑一个具有非均匀温度场的物系的“内部熵”问题,而这和热力学一贯的平衡态思路是矛盾的。
http://s3.album.sina.com.cn/pic_3/5562bb43020014wq比如,在一个有限的时间内,我们可以把地心、地幔、地壳看作是各自温度均匀的子物系考虑其各层的熵吗?整个地球的熵是这三个子结构的熵的加和吗?如果回答“熵不可以逐点计算”,那么意味着(一)和(二)当中不存在各个子物系的熵的问题,因为子物系就是总物系中的一个“点”,既然独立的、处于平衡态的子物系没有熵的问题,为何还说熵是物系的状态函数?也就是说,熵和物系的状态既然不是逐一对应的关系,那么还叫作什么状态函数?同样如果(一)和(二)中各子系都没有熵,那么,也就不存在“总熵”问题,同样从(一)到(二)也就没有熵变化⊿Sa、⊿Sb、⊿Sc……、⊿Sa+b+c+……可言了。
这个实验揭示的科学方法原则是:绝不可以把一个物系的状态函数定义在和其它物系之间的关系之上。或者说,态函数是对物系自身状态的描述,应与其它物系的状态无关。
热力学怎么看待一个状态点上的熵这个问题?热力学教材会描述到:物系的熵是有绝对值的,但是通常不需要计算熵的绝对值,只需要计算熵的变化。显然,这种表述是在出现内部逻辑问题之后的托辞。通常的教科书的叙述是,任意状态点(T,P,V)上的熵可以表示为S=∫dQ/T+S0,其中S0被成为“基态”,是任意选取的一个参数。然而,基态的熵任意取值就意味着S也是任意取值的,换句话说,任意状态下的熵是不可计算和确认的。
这种计算状态点上的熵的说法其实就是一直狡辩,说来说去还是计算熵差而非计算熵变,即描述的始终是一个过程而非一个状态点。基态和过程起点完全是两个概念,前者是针对增长过程而言的,后者是一个硬性规定的计量0点。这就像我们要知道一栋大楼本周末盖到多少层,而对方的回答始终是“本周盖了3层”,而拒绝回答到了第几层这个问题。“本周盖了3层”意味着一个增量,以上周的层数S0为基点,现在是第S0+3层了,本周的工程量为(S0+3)-S0=3层,和S0取值大小无关;但是,“本周盖到第N层”之“N”的基准是地面层为1,即S0=1,这是不可更改的规定。如果这个规定改变了,这个问题就没有办法回答了。例如有国家把地面层叫做0楼(GROUND),即S0=0,第二层叫做1楼。在两套约定之下,楼层算是几楼就成了一个谜团了。
再例,我有个朋友非常幽默,别人问他“今天星期几?”,他总是回答之前一本正经地反问“昨天星期几?”。如果已知“昨天星期几”还有“今天星期几”之问吗(智障除外)?换句话说,如果昨天这个“基态”S0是可以任意取值的,就不存在对“今天”这个点S的定量测度了。
如果认可S=∫dQ/T+S0这种所谓的计算点熵的办法,我们就会发现一个奇怪的现象:对热力学的状态参数E、P、V、T、H当中的每一个我们都可以谈论“变化率”这个概念,例如内能增大百分之几、压力增大百分之几、体积减少百分之几、温度升高百分之几等等。但是,惟独无法回答“熵增加率”的问题,因为熵增加率=S/S0-1,S0可以任意取值,就意味着熵的增加率是无法描述的,因为基于不同基点的同一个增量的增长率是不同的。我们可以计算增长量,却竟然无法考虑增长率的问题,这岂不怪哉?
从玻尔兹曼对熵的理解S=klogW来说,物系处于任意状态点的时候,都应该有一个可以确定的W值,如果说So是任意指定为零的,就意味着物系的微观分布W也是可以随意指定的,也就是说,不存在所谓的混乱程度或均匀度这种概念了。
我们应该认识到,热力学符号系统是一个整体,由于T0、V0、P0不是任意取值的,所以S0=S(T0、V0)也不可以任意取值,否则就意味着不存在S和(T,V)的对应关系,即S不是状态点的函数了。
热力学的狡辩其实就是把作为微积分基本定理的“牛顿-莱布尼兹公式”做了一个缪用。在“牛顿-莱布尼兹公式”∫abf(x)dx=F(b)-F(a)中,给定一个起始状态点a,必定有一个状态函数点F(a),它不是可以任意取值的。原函数F(x)的存在性就决定了它是和任意一个区间[a,b]内的x值逐一对应的,不管是起点a还是终点b,没有在起点a的任意取值之说。
(请续看下帖)
 爱华网
爱华网