二、一维场空间的一般性质
1、隐形效应由一维场空间的基本性质,我们不难发现它的一个奇特效应——隐形效应。就是说,所有进入一维场空间的实物粒子,都是沿一维场线作同速同向运动的。这里的实物粒子包括质子、中子、电子、光子等所有的基本粒子,它们的运动状态都是相同的,没有任何粒子会偏离一维场线,连光子也不能。对于一维场空间外的观察者来说,由于没有任何粒子会从一维场空间射出,你得不到关于一维场空间的任何信息。所以,一维场空间对于外来的观察者来说是隐形的、是看不到的。你得不到关于一维场空间的任何信息,你怎么会观察到一维场空间以及其中运动的物质呢?不仅生命体观察不到,生命体制造的各种探测仪器也探测不到。就是说,一维场空间具有隐形性,具有不可测性。我们认为,用一维场空间理论可以解释世界上的一大批失踪案件,例如,百慕大三角海域的神秘失踪案件等等。2、场化效应
由于一维场空间内运动的所有物质的运动状态(方向、速度)都是相同的,这就决定了它们的存在形态都必然相同。因为,现有的科学事实告诉我们,运动状态相同的物质,必然属于同一形态。那么,在一维场空间内运动的物质粒子都以什么形态存在呢?我们说,都以场的形态存在。为什么这样说呢?我们可以先从光子谈起。我们知道,光子具有场粒二象性。它和实物粒子作用时显粒子性,在运动过程中呈场性。一维场空间中的光子是运动着的,因此,它必然以场的形式存在。由于,其它物质粒子的运动状态和光子相同,所以,我们可以断定,其它物质粒子也必然以场的形式存在。不仅如此,而且它们的运动速度也必然等于光速。就是说,一维场空间具有场化效应。由此,我们还可以推论:如果一个运动物体的运动速度达到了光速,那么,它必然是场。它必然是以场的形式存在。现在,人们幻想到宇宙空间去旅行,幻想制造出光子火箭来。从场论的观点看,以光速运动的实物体是不存在的。如果,一个实物体的运动速度达到了光速,那么,它早就场化了。飞碟的来无影去无踪,正和场化有关。就是说,我们要解决光速旅行问题,必须先解决场化问题。必须象神话所说的那样——化作万道金光。
3、时间效应
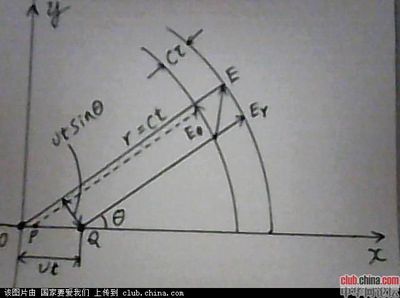
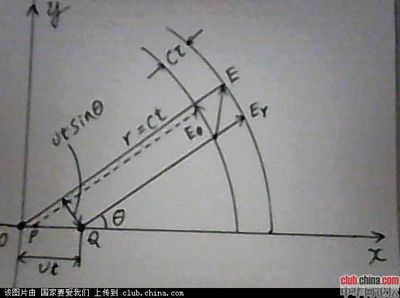
1968年5月3日,美国国家航空公司的一架大型客机,连同飞机上的机组人员全部在百慕大三角上空消失了。地面雷达搜遍整个天际,也找不到它的踪影。10分钟后,正当人们心情万分焦急的时候,这架飞机却在天空突然出现了。然而,当飞机在机场安全着陆后,人们却发现了一个奇怪的事实:飞机上所有人员的一切时间记录器,例如手表、怀表等等,统统都比陆地上人们的时间指示器慢了10分钟,机上的人员一点也不知道这异常的变化。怎么解释这件事呢?科学家桑德松认为,飞机到时间停止的类宇宙去经历过去和未来了。但从场论的观点看,这架飞机是进入了一维场空间(或者类似的场化空间)。飞机的重新出现说明这个一维场空间是环状开口的(如图):
飞机进入一维场空间被场化。
飞机出来一维场空间重新被实化。 飞机进入一维场空间被场化。 飞机出来一维场空间重新被实化。
飞机从一端进去,从另一端出来。在这个过程中,时间不是停止不动了,而是照常在流淌。时间表面上看起来是凝止不动了,其实不然。其根本原因,就是因为在一维场空间运动的一切物体的基本粒子都以同种状态,即同速同向运动,相对位置保持不变。这样的必然结果是:生命体失去了感知能力,不能感知时间了;生命体的制造物——各种时间记录器包括手表、怀表等等,也都失去了记录时间和描述时间的能力。这就必然会出现客观的时间凝固,主观的无感知时间的正常流动现象了。这就是一维场空间的时间效应:主观的不被感知,客观的时间凝固。
由此,我们也可以得到一个重要推论:一维场空间不存在生命现象。
这就是一维场空间的一般效应。

三、低维空间
除了一维场空间外,二维场空间、三维场空间等等简单的低维空间。我们在这里只讨论一下二维场空间的结构和性质。我们认为,如果二维场空间果真存在的话,它必然具有两种基本结构:①在一维场空间的基础上,又有一个附加的环形场;②在一维场空间的基础上,有一个和一维场垂直的场。如图甲、乙:
图甲 图乙
如果考虑第二种场的方向性的话,环形场又应有顺时针和逆时针两种结构类型;而直线场则应有一个在一维场方向上周期性出现的反方向场。就是说,对于二维场空间,我们目前至少可以指出三种基本类型。
我们可以这样来研究二维场空间的性质。设想把一个实物粒子放入二维场空间。那么,在有环形场存在的二维场空间,这个实物粒子一方面要沿一维场线运动,另一方面要沿环形场线运动。这样,这一实物粒子的运动曲线必然呈螺旋运动曲线。这种螺旋运动曲线也一定有左旋和右旋两种情况:
左旋 右旋
而在直线型二维场空间内,实物粒子的运动曲线至少有
一种正弦曲线:
至于螺旋线的半径大小以及正弦线的振幅大小,还应受实物粒子的初速度及其它性质的影响。也有可能,二维场空间内,有的粒子只受这种场化影响,而另外的粒子只受另一种场影响,从而出现物质运动形式的多样化。就是说,二维场空间内,物质粒子的运动形式远比一维场空间要复杂的多。
至于三维场空间及其它低维场空间的性质,我们在这里就不进行讨论了。
 爱华网
爱华网