管理咨询实践中经常会遇到在某企业在实施某项变革措施后,职工对变革的认可程度的调查。下边举一个例子,说明统计技术在这类调查中的应用。
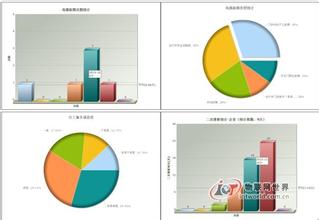
某企业实施了新的薪酬方案一段时间之后,聘请咨询公司从全体员工中抽样60名员工,做了一次员工对新的薪酬方案的满意度调查,征求员工对薪酬方案的意见。调查其中的一个项目是,您对新的薪酬方案的总体评价如何?有三个选项:赞成、反对、不置可否。调查的结果是23人赞成,19人不置可否,18人反对。您如果是咨询项目组的成员,您对这个调查项目将做什么结论呢?能否说全体员工中持赞成态度的人比持其他态度的人多呢?
简单地看,选择赞成的人数比较多,各种答案的选择人数不等。但因为这是抽样研究(在企业中调查时,很难100%的调查全体人员),选择各种答案的人数不等可能由两个原因造成:1、全体员工确实选择各种答案的人数不等;2、全体员工选择各种答案的人数实际上是相等的,由于抽样范围造成了不等。为了推论全体员工的态度,就需要使用统计中的卡方检验技术。检验过程如下:
首先提出全体员工的选择各答案人数相等的假设。在假设条件下,多次对60人调查,选择每种答案的期望平均人数应该是20人(60/3=20),用fe表示。将每个答案实际选择的人数:23,19,18,用fo表示。
服从卡方分布(指如果假设成立,即全体员工选择各答案的人数实际如果相等的话,仅由于随机因素造成卡方值落入某一数值区间的概率分布)。在显著性水平(说明随机原因造成卡方值落入某一小概率区间的概率值)α=0.05,自由度为2时,临界值(随机原因造成卡方值大于临界值的概率为以上显著性水平5%,是小概率事件,此值可以查表得到)为5.99。根据上述调查计算取得的实际卡方值为0.7。0.7<5.99表示小概率事件没发生,接受假设,推断出总体选择各答案的人数相等。
其含义是,根据实际卡方值和理论卡方值的比较,我们有95%的概率把握说明全体员工选择赞成、否定和不置可否的人数相等,也就是说满意和不满意的人数都不突出,新薪酬方案跟原薪酬方案比,员工满意度没有太大的变化。 至于卡方分布的具体含义,请大家翻翻统计学原理教科书。 爱华网
爱华网