用数轴上的一段经历或一个数据区间,表示总体参数的可能范围.这一段距离或数据区间称为区间估计的置信区间
区间估计(interval estimation)是从点估计值和抽样标准误出发,按给定的概率值建立包含待估计参数的区间.其中这个给定的概率值称为置信度或置信水平(confidence level),这个建立起来的包含待估计函数的区间称为置信区间(confidence interval),指总体参数值落在样本统计值某一区内的概率;而置信区间是指在某一置信水平下,样本统计值与总体参数值间误差范围。置信区间越大,置信水平越高。划定置信区间的两个数值分别称为置信下限(lower confidence limit,lcl)和置信上限(upper confidence limit,ucl) 区间估计的区间上、下界通常形式为:“点估计±误差” “总体均值”的区间估计 ● 符号假设: 总体均值:μ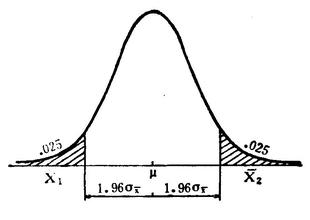
总体方差:σ 样本均值:x* =(1/n)×Σ(Xi) 样本方差:s* =(1/(n-1))×Σ(Xi-x*)^2 置信水平:1-α 显著水平:α ● 问题:已知n个样本数据Xi (i=1,2,...,n),如何估计总体的均值? 首先,引入记号: σ‘=σ/sqrt(n) s‘=s*/sqrt(n) 然后,分情况讨论: 情况1 小样本(n<30),σ已知,此时区间位于 x* ± z(α/2)×σ‘ 情况2 小样本(n<30),σ未知,此时区间位于 x* ± z(α/2)×s‘ 情况3 大样本(n≥30),σ已知,此时区间位于 x* ± z(α/2)×σ‘ 情况4 大样本(n≥30),σ未知,此时区间位于 x* ± t(α/2)×s‘ 其中, z(α/2)表示:正态分布的水平α的分位数 t(α/2)表示:T分布的水平α的分位数
 爱华网
爱华网