一、教学目标:
1.知识目标:
①能准确理解的几何意义和代数意义。
②能准确熟练地求一个有理数的。
③使学生知道是一个非负数,能更深刻地理解相反数的概念。
2.能力目标:
①初步培养学生观察、分析、归纳和概括的思维能力。
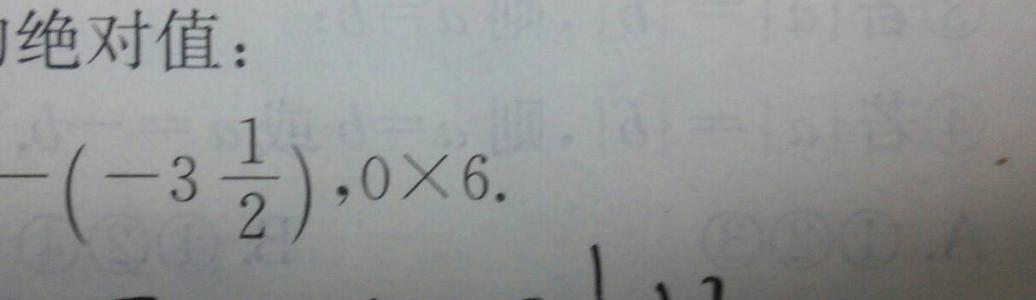
②初步培养学生由抽象到具体再到抽象的思维能力。
3.情感目标:
①通过向学生渗透数形结合思想和分类讨论的思想,让学生领略到数学的奥妙,从而激起他们的好奇心和求知欲望。
②通过课堂上生动、活泼和愉快、轻松地学习,使学生感受到学习数学的快乐,从而增强他们的自信心。
二、教学重点和难点
教学重点:的几何意义和代数意义,以及求一个数的。
教学难点:定义的得出、意义的理解及求一个负数的。
三、教学方法
启发引导式、讨论式和谈话法
四、教学过程
(一)复习提问
问题:相反数6与-6在数轴上与原点的距离各是多少?两个相反数在数轴上的点有什么特征?
(二)新授
1.引入
结合教材P63图2-11和复习问题,讲解6与-6的的意义。
2.数a的的意义
①几何意义
一个数a的就是数轴上表示数a的点到原点的距离。数a的记作|a|。
举例说明数a的的几何意义。(按教材P63的倒数第二段进行讲解。)
强调:表示0的点与原点的距离是0,所以|0|=0。
指出:表示“距离”的数是非负数,所以是一个非负数。
②代数意义
把有理数分成正数、零、负数,根据的几何意义可以得出的代数意义:一个正数的是它本身,一个负数的是它的相反数,0的是0。
用字母a表示数,则的代数意义可以表示为:<?xml:namespace prefix =v ns ="urn:schemas-microsoft-com:vml" /><?xml:namespace prefix =o ns ="urn:schemas-microsoft-com:office:office" />
指出:的代数定义可以作为求一个数的的方法。
3.例题精讲
例1.求8,-8,,-的。
按教材方法讲解。
例2.计算:|2.5|+|-3|-|-3|。
解:|2.5|+|-3|-|-3|=2.5+3-3=6-3=3
例3.已知一个数的等于2,求这个数。
解:∵|2|=2,|-2|=2
∴这个数是2或-2。
五、巩固练习
练习一:教材P641、2,P66习题2.4A组1、2。
练习二:
1.小于4的整数是____。
2.最小的数是____。
3.已知|2x-1|+|y-2|=0,求代数式3x2y的值。
六、归纳小结
本节课从几何与代数两个方面说明了的意义,由的意义可知,任何数的都是非负数。的代数意义可以作为求一个数的的方法。
七、布置作业
教材P66习题2.4A组3、4、5。
 爱华网
爱华网