线性规划是运筹学中研究较早、发展较快、应用广泛、方法较成熟的一个重要分支,它是辅助人们进行科学管理的一种数学方法。研究线性约束条件下线性目标函数的极值问题的数学理论和方法,英文缩写LP(LP[linear programming),中学时期传统的做法是作图,平移目标函数来求解。这里以一个简单例程介绍如何利用Excel进行线性规划求解
利用Excel求解线性规划问题――工具/原料Excel利用Excel求解线性规划问题――方法/步骤
利用Excel求解线性规划问题 1、
在Excel中加载规划求解模块。Excel2010的步骤是:文件->选项->加载项->转到->勾选上“规划求解加载项”。
利用Excel求解线性规划问题 2、
看题理解后进行数学建模,然后将模型和数据输入在Excel的单元格中。本例的题目为:某工厂在计划期内要安排生产Ⅰ、Ⅱ两种产品,已知生产单位产品所需的设备台时及A、B两种原材料的消耗,如表2-1所示。该工厂每生产一件产品Ⅰ可获利2元,每生产一件产品Ⅱ可获利3元,问应如何安排计划使该工厂获利最多?生产产品I需耗时1单位,生产产品II需要耗时2单位时间,总的单位时间不超过8单位,产品I消耗原料A 4个单位,产品II消耗原材料B 4个单位,其中原料A有16kg,原料B有12kg。建模情况在Excel中表现为附图所示:
利用Excel求解线性规划问题_线性规划
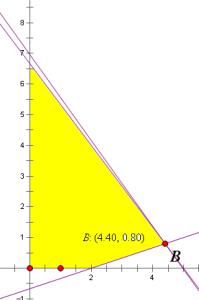
利用Excel求解线性规划问题 3、
Excel进行线性规划求解过程如下:1.使用相关函数和运算符表示约束条件和目标函数;2,使用数据中的规划求解模块对已经建好的模型进行数学运算求解。a,选择目标函数区域 b,选择可变参数区域 c,选择并定义约束条件 d选择求解方法,本例采用单纯线性规划。然后确定求解即可。
利用Excel求解线性规划问题_线性规划
利用Excel求解线性规划问题_线性规划
利用Excel求解线性规划问题 4、
最后在Excel的单元格中会自动填充运算得出的最优化方案。本例中的的最优解为:生产产品I 4件,生产产品II 2 件时得到最大利润14元。
 爱华网
爱华网