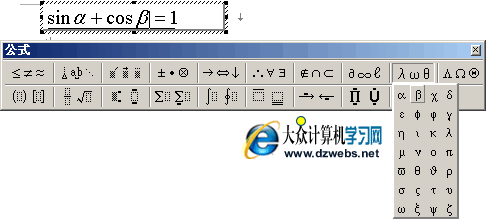
贝塔分布(Beta Distribution) 定义如下:其中是贝塔函数,其定义为:是伽玛函数,贝塔分布是一个作为伯努利分布和二项式分布的共轭先验分布的密度函数,在机器学习和数理统计学中有重要应用。贝塔分布中的参数可以理解为伪计数,伯努利分布的似然函数可以表示为,表示一次事件发生的概率,它为贝塔有相同的形式,因此可以用贝塔分布作为其先验分布。
贝塔分布_贝塔分布 -贝塔(β,beta)分布
概率论中还有一种称为贝塔(β,beta)分布的概率密度分布函数。它的数学形式是
贝塔分布
,00,q>0 (18.25)
这里的变量x仅能出现于0到1之间,p,q是两个大于0的参数。B(p,q) 的含义是
(18.26)
它与Γ函数,有如下关系
(18.27)
而我们介绍过的阶乘符号!与Γ的关系是
n!= Γ(n+1)
所以贝塔分布也可以写为
(18.28)
现在考虑从最复杂原理加适当的约束条件推求这个概率密度分布函数的问题。根据过去的经验,容易看出它可能是下面两个约束条件与最复杂原理的应用结果。
变量x的对数的平均值为固定值(等价于几何平均值为常数):
(18.29)
(1-x)的对数的平均值也是固定之值:
(18.30)
作为概率密度,当然还有
(18.31)
根据上面的三个约束公式和最复杂原理,利用拉哥朗日方法,构造的F函数是
求F对未知的概率密度f的偏微商,并且令它等于0(利用了最复杂原理),我们得到
利用分布函数的积分应当等于1的约束和积分知识我们得到
所以分布函数可以写为
(18.32)
显然,这个公式的外型已经与贝塔分布一致了。余下的问题是利用关于u,v的约束公式可以求出C2,C3 。使这个公式通过u,v来表示。由于u,v与C2,C3的关系比较复杂,我们没有得到具体的关系式。但是概率密度分布函数的形状与概率论中的贝塔分布一致就已经达到了我们的目的:界于0-1之间的变量的两种几何平均值固定和最复杂原理相结合可能是一些贝塔分布形成的原因。
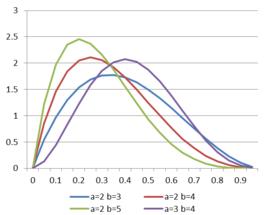
贝塔分布中的变量x的变化范围仅能在0到1之间,而且(1-x)与x有对称性,这是重要的特点。图18.5给出了p=3,q=6时的贝塔分布函数的形状。
图18.5贝塔分布的曲线形状
贝塔分布_贝塔分布 -实例
空气中含有的气体状态的水分。表示这种水分的一种办法就是相对湿度。即现在的含水量与空气的最大含水量(饱和含水量)的比值。我们听到的天气预告用语中就经常使用相对湿度这个名词。
相对湿度的值显然仅能出现于0到1之间(经常用百分比表示)。而空气为什么出现某个相对湿度显然具有随机性(可以利用最复杂原理),这些提示我们空气的相对湿度可能符合贝塔分布。
马淑红等人完成的“塔里木气候极值及其在油田工程设计中的应用”研究中(同名的书由气象出版社于1995年出版见138-142页),刘绍民等人分析了冬季塔里木盆地的日最大相对湿度和夏季日最小相对湿度。证实它们都符合贝塔分布。
 爱华网
爱华网