地球的半径是从地球中心的距离到其表面在卑鄙海平面。地球不是一个规则的物体。首先,它不是正球体,而是椭球体,准确地说是一个两极稍扁,赤道略鼓的扁球体;其次,地球的南极、北极也不对称,就海平面来说,北极稍凸,南极略凹;第三,地球的外部地形起伏多变(这对测量地球半径是没有影响的)。地球半径有时被使用作为距离单位,特别是在天文学和地质学中常用,它通常用RE表示。地球大概半径为6371.004千米。随着科学的发展,人们对地球的认识也越来越深入,并发现地球不完全是球形的,而是一个椭球体。
地球半径_地球半径 -简介
地球这种不规则的形状意味着在不同的地方测量,其半径也不同。
地球半径_地球半径 -测定方法
方法一
地球半径
我们知道,地球的形状近似一个球形
,那么怎样测出它的半径呢?据说公元前三世纪时希腊天文学家厄拉多塞内斯(Eratosthenes,公元前276―前194)首次测出了地球的半径。
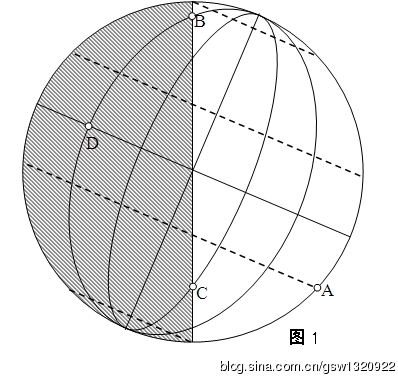
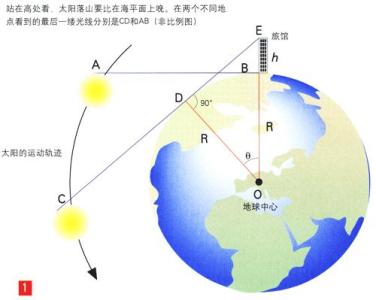
他发现夏至这一天,当太阳直射到赛伊城(今埃及阿斯旺城)的水井S时,在亚历山大城的一点A的天顶与太阳的夹角为7.2°(天顶就是铅垂线向上无限延长与天空“天球”相交的一点)。他认为这两地在同一条子午线上,从而这两地间的弧所对的圆心角SOA就是7.2°(如图1)。又知商队旅行时测得A、S间的距离约为5000古希腊里,他按照弧长与圆心角的关系,算出了地球的半径约为40000古希腊里。一般认为1古希腊里约为158.5米,那么他测得地球的半径约为6340公里。
其原理为:
地球半径
设圆周长为C,半径为R,两地间的的弧长为L,对应的圆心角为n°。
因为360°的圆心角所对的弧长就是圆周长C=2πR,所以1°的圆心角所对弧长是2πR/360,即πR/180。于是半径为的R的圆中,n°的圆心角所对的弧长L为:
l=n*πR/180 ∴R=180L/(nπ)
当L=5000古希腊里,n=7.2时,
R≈180*5000/(7.2*3.14)=40000 (古希腊里)
化为公里数为:(公里)
40000*158.5/1000=6340 (公里)
厄拉多塞内斯这种测地球的方法常称为弧度测量法。用这种方法测量时,只要测出两地间的弧长和圆心角,就可求出地球的半径了。
方法二
地球半径
近代测量地球的半径,还用弧度测量的方法,只是在求相距很远的两
地间的距离时,采用了布设三角网的方法。比如求M、N两地的距离时,可以像图2那样布设三角点,用经纬仪测量出△AMB,△ABC,△BCD,△CDE,△EDN的各个内角的度数,再量出M点附近的那条基线MA的长,最后即可算出MN的长度了。
通过这些三角形,怎样算出MN的长度呢?这里要用到三角形的一个很重要的定理――正弦定理。
即:在一个三角形中,各边和它所对角的正弦的比相等。就是说,在△ABC中,有a/sinA =b/sinB =c/sinC。
在图2中,由于各三角形的内角已测出,AM的长也量出,由正弦定理即可分别算出:
地球半径
∴M
N=MB+BD+DN。
如果M、N两地在同一条子午线上,用天文方法测出各地的纬度后,即可算出子午线1°的长度。法国的皮卡尔(Pi-card.J.1620―1682)于1669―1671年率领他的测量队首次测出了巴黎和亚眠之间的子午线的长,求得子午线1°的长约为111.28公里,这样他推算出地球的半径约为6376公里。(R≈111.28*180/3.1416≈6376(公里))
另外,布设三角网有多种方法,要根据实际情况,布设的网点越少越好。
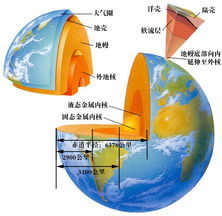
随着科学的发展,人们对地球的认识也越来越深入,并发现地球不完全是球形的,而是一个椭球体(如图3)。科学家家们还找到了求得地球的长半径a和短半径b的方法,由于比较复杂,我们这里就不介绍了,有兴趣的同学可阅读有关书籍。
地球半径_地球半径 -常用值
极半径
从地心到北极或南极的距离,大约3950英里(6356.9088千米)(两极的差极小,可以忽略)。
赤道半径
是从地心到赤道的距离,大约3963英里(6377.830千米)。
平均半径
大约3959英里(6371.393千米)。这个数字是地心到地球表面所有各点距离的平均值。
可以这样求:平均半径=(赤道半径×2+极半径)/3
地球半径有时被使用作为距离单位,特别是在天文学和地质学中常用。它通常用RE表示。
地球大概半径6370.856千米。
 爱华网
爱华网