正整数为大于0的整数。自然数中,除了0就是正整数。正整数又可分为素数,1和合数。
正整数_正整数 -定义
整数是不包括小数部分的数且包括“-1、-2、-3……”一类的数,正整数是指大于0的整数。例如1,2,3等可以用来表示完整计量单位的对象个数的数,是正整数。
正整数_正整数 -正整数的符号
N+(或N*)
正整数_正整数 -整数分类
我们以0为界限,将整数分为三大类 :
1.正整数,即大于0的整数,如,1,2,3,…,n,…2.0 既不是正整数,也不是负整数(0是整数)。
3.负整数,即小于0的整数,如,-1,-2,-3,…,-n,…
为什么如此分类呢?
简单的说,就是这三类数有质的不同,即本质区别。
正因为如此,这种分类就很稳定,也很实用,可用于推理的分类判断环节。
说得有点抽象了,自己以后慢慢体会它的好处了。
利用皮亚诺公理就可以定义了:
①1是正整数;
②每一个确定的正整数a,都有一个确定的后继数a' ,a' 也是正整数(一个数的后继数就是紧接在这个数后面的数,例如,1的后继数是2,2的后继数是3等等);
③如果b、c都是正整数a的后继数,那么b = c;
④1不是任何正整数的后继数;
⑤任意关于正整数的命题,如果证明了它对正整数1是对的,又假定它对正整数n为真时,可以证明它对n' 也真,那么,命题对所有正整数都真。(这条公理也叫归纳公设,保证了数学归纳法的正确性)
正整数_正整数 -正整数的分类
我们知道正整数的一种分类办法是按照其约数或积因子的多少来划分的,比如仅仅有两个的(当然我们总是多余地强调这两个是1和其本身),我们就称之为质数或素数,而多于两个的就称之为合数。
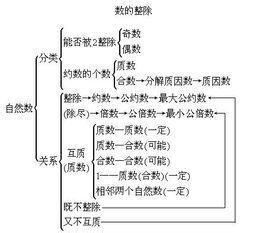
我认为这样的划分办法应该再进一步地完善,理由一:既然是以约数的个数来划分的,就应该按照这个参照把整个正整数分类完毕。比如按照老的分类办法就把1排除在外了,这么重要的数结果落的个即不是合数,也不是质数。理由二:分类不够详细,有四个及其以上约数的还应该再继续划分下去。理由三:把偶数和奇数的概念也包括进去。
这样的话,正整数的分类就为如下样式:
一、按照约数的个数划分:
一个约数的称之为一合数,比如1。二个约数的称之为二合数,即目前的质数。
三个约数的称之为三合数,即目前的合数的一部分。
四个约数的称之为四合数,即目前的合数的一部分。
五个……
……
二、按照约数的性质划分:
约数是或含2的称之为偶合数。约数非或无2的称之为奇合数。
另,这样,哥德巴赫猜想一搞,就表述为:一个足够大的偶合数(大于等于6)都可以表示为两个奇质数之和。”
正整数_正整数 -一些基本的结论:
正整数的唯一分解定理:又称为算术基本定理
即:每个大于1的自然数均可写为质数的积,而且这些素因子按大小排列之后,写法仅有一种方式。离散不等式:若X,N为整数,X>N,则等价于X≥N+1
 爱华网
爱华网