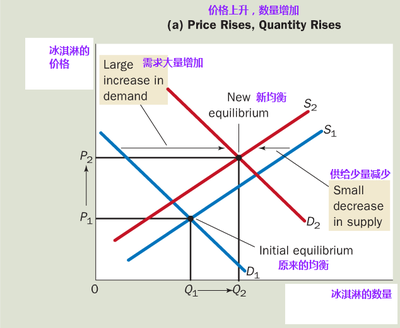
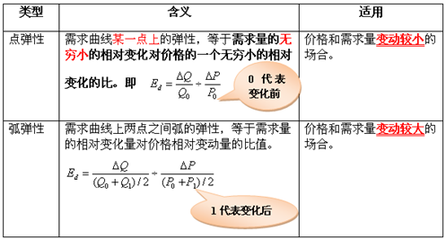
需求价格弹性(Price elasticity of demand),简称为价格弹性或需求弹性,需求价格弹性:是指需求量对价格变动的反应程度,是需求量变化的百分比除以价格变化的百分比。需求量变化率对商品自身价格变化率反应程度的一种度量,等于需求变化率除以价格变化率。
需求价格弹性_需求价格弹性 -公式
用数学术语就是:
需求价格弹性
需求弹性 = 需求量变化的百分比÷价格变化的百分比
即需求量变化的百分比除以价格变化的百分比。需求的价格弹性实际上是负数;也就是说,由于需求规律的作用,价格和需求量是呈相反方向变化的,价格下跌,需求量增加;价格上升,需求量减少。因此,需求量和价格的相对变化量符号相反,所以需求价格弹性系数总是负数。由于他的符号始终不变,为了简单起见,习惯上将需求看做为一个正数,因为我们知道它是个负数。
需求价格弹性_需求价格弹性 -基本类型
当 需求量变动百分数大于价格变动百分数,需求弹性系数大于1时,叫做需求富有弹性或高弹性;
当 需求量变动百分数等于价格变动百分数,需求弹性系数等于1时,叫做需求单一弹性;
当 需求量变动百分数小于价格变动百分数,需求弹性系数小于1时,叫做需求缺乏弹性或低弹性。
需求价格弹性_需求价格弹性 -含义
弹性理论的目的在于说明价格变化 比率与 需求量(或 供给量)的变动比率之间的关系。
需求弹性的概念:影响 需求量的某因素(自变量)的值每变动百分之一,所引起 需求量变化的 百分率。即:
一、需求价格弹性
1、定义
价格的值每变动百分之一而引起 需求量变化的 百分率。通常,用价格变动的 百分率引起 需求量变化的百分率来表示。这两个 百分率的比值,称为 弹性系数,记为Ep,即:
Ed的性质
(1) Ed的 数值,不随选用的计量单位而变化。
(2) Ed的 数值,可能为正数、负数、等于0或等于1。依赖于有关两个变量是同方向变化,还是反方向变化。
Ed为正还是为负,所表示的仅仅是有关变量变化的方向性关系,而Ep的 绝对值的大小则表示了变化程度的大小。有时,为了便于比较弹性值的大小,在等式右端添加一个负号,使其成为正值。通常用 绝对值的大小来表示价格变动对 需求量变动的影响程度。当我们说,某产品的需求价格弹性大,即指其 绝对值大。
(3) Ed的 数值,随 商品的不同而不同。即使在同一种 商品的一条既定的需求 曲线上,也随价格不同而不同。
Ed的变动范围
(1) Ed=1(单位需求价格弹性)。说明 需求量变动幅度与价格变动幅度相同。即价格每提高1%, 需求量相应地降低1%。反之则反是。
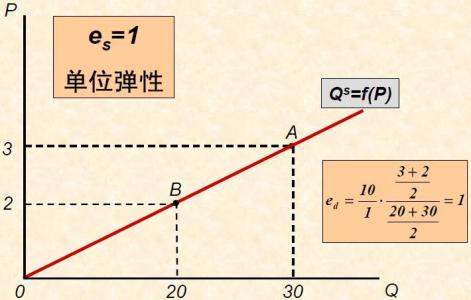
需求曲线特点:等轴双曲线或正双曲线。需求方程:PQ=K( 常数)。
(2) 1<Ed<∝(需求富有弹性)。说明 需求量变动幅度大于价格变动幅度(ΔP/P<ΔQ/Q=。即价格每变动1%, 需求量变动大于1%。
需求曲线特点:比较平坦( 斜率较小)。
(3) 0<Ed<1(需求缺乏弹性)。 说明 需求量变动幅度小于价格变动幅度(ΔP/P>ΔQ/Q)。即价格每变动1%, 需求量变动的 百分率将小于1%。
需求曲线特点:较陡( 斜率较大)。
(4) Ed→0(需求完全无弹性)。此时,意味着ΔQ/Q=0。在这种情况下,需求状况具有如下特点: 需求量不随价格的变动而变动。需求函数的形式为:Q=K(任意既定 常数)。在二维空间图上, 需求曲线是一条垂直于横 坐标的直线,在横坐标上截距等于K(=Q0)。这表示不管价格怎样变动, 需求量总是固定不变。即不管ΔP的 数值如何,ΔQ之值总是为零。这种情况是罕见的。
(5) Ed→∝(需求完全有弹性),此时,ΔP/P→0。在这种情况下,需求状况具有如下特点:在既定价格之下, 需求量可以任意变动。需求函数的形式为:P=K( 常数)。 需求曲线将是一条与横 坐标平行的直线,与横坐标的距离,既定为 常数K(=P0)。这种情况也是罕见的。在现实生活中,自由市场上某些同质的产品,由于竞争的结果,都按同一价格出售,基本属于这类 需求曲线的例子。
需求价格弹性的数学计算
(1) 一般计算法。计算公式为:
根据上述公式计算的弹性值,虽然ΔQ与ΔP的 数值相同,但据以计算价格变动 百分率(ΔP/P)的P和据以计算 需求变动百分率(ΔQ/Q)的Q,在两种场合(价格上升、价格下降)各不相同。就是说,虽然价格变动的 绝对值与由此引起的 需求量变动的绝对值相同,只是由于计算的基础不同,所以得出的弹性值也就不同。
为解决上述问题,可采用另一种计算方法。即把计算价格变动的 百分率所用价格用变动前后两个价格的算术平均数来代替,而计算 需求变动百分率的 需求量则用变动前后两个需求量的算术平均数来代替。这样,不管从价格向下降落还是从价格向上提高出发,据以计算变动 百分率的P和Q的 数值相同,于是得出 弹性系数的另一种计算方法,即求 弧弹性。
(2) 求 弧弹性。 求 弧弹性,即要计算 需求曲线上某两点之间一段弧的平均弹性。因而称之为弧 弹性系数。如果不知道 需求曲线方程,只知道需求曲线上两点的 坐标(更多的属于这种情况)。只要 假定在两次数据观察之间,所有别的影响需求的变量保持不变,则可由上式求得弧 弹性系数。
需要指出:要使价格向下与价格向上时的Ep一致,取价格的小者,数量的小者为基数,也可得到Ep值相同的结果。
(3) 求 点弹性 若需求函数为已知,即可根据上式求出任一价格下的点 弹性系数。
例:设某 商品的需求函数为:Q= 30-5P
∵dQ/dP=-5
∴EP=|-5×P/Q|=5P/(30-5P)
这表明 点弹性EP是价格P的函数。
若P=2,则Q=20→EP=0.5
若P=3,则Q=15→EP=1.0
若P=4,则Q=10→EP=2.0
结论:对一个既定的需求函数,在不同的价格之下会有不同的弹性值。
图2-5中,B为中点,当BC=AB时,EP=1;
当BCB→C时,因BC→0,所以EP→0;
当BC>AB时,EP>1,位于B点左上方任一点的弹性系数的绝对值大于1,而且距A点越近的弹性系数,其绝对值越大;
当B→A时,因BA→0,所以EP→∝。
价格弹性与需求曲线的斜率是两个不同的概念,但二者有所联系。价格弹性与需求曲线的斜率ΔP/ΔQ成反比,与P/Q的值成正比。因此,如果需求曲线是一条<a>直线,尽管这条直线上各点的 斜率不变,但由于P/Q的值是变动的,所以这条直线上的价格弹性也是变动的。但如果其它条件相同,那么,平坦的需求曲线弹性大,陡的需求曲线弹性小。
(4)需求价格弹性的几何求法
当 需求曲线为直线时,可以证明B点的 点弹性为BC/AB。
已知价格弹性的公式为:
ΔQ=LM=GH;Q=OL;
ΔP=EF=BG;P=OE。
代入①式得:
GH OE
Ep= ―― · ―― ②
BG OL
∵ΔBGH~ΔBLC,BL=OE
GH LC LC
∴――=――=――
BG BL OE
代入②式得:
LC OE LC BC
Ep=―― · ――=――=――
OE OL OL AB
∵ΔAEB~ΔBLC (BE=OL)
LC BC LC BC
∴――=―― ――=――
BE AB OL AB
5、Ep与TR之间的关系
P
Ep>1
Ep=1
Ep<1
P上升
TR减少
TR不变 TR增加
P下降
TR增加
TR不变 TR减少
Ep>1时,P、TR反方向变动;
Ep<1时,P、TR同方向变动。
 爱华网
爱华网