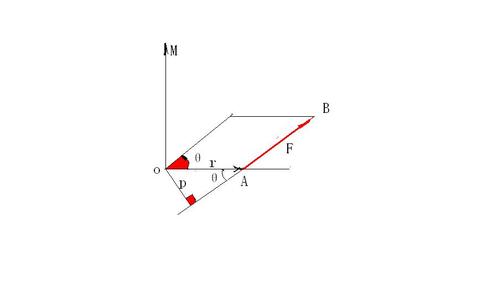
向量积也被称为矢量积、叉积(即交叉乘积)、外积,是一种在向量空间中向量的二元运算。与点积不同,它的运算结果是一个伪向量而不是一个标量,两个向量的叉积与这两个向量垂直,其运算结果叫叉积(即交叉乘积)、外积或向量积。向量积:在三维坐标系中,从坐标原点O沿X轴取向量OA=a,沿Y轴取向量OB=b.从原点OC垂直与OAB平面,其向量积OC=a*b,其方向由右手法则确定右手拇指指向OA,食指指向OB,中指指向OC。即c的长度在数值上等于以a,b,夹角为θ组成的平行四边形的面积。
向量积_向量积 -方程式
向量积
两个向量a和b的叉积写作a×b(有时也被写成a∧b,
避免和字母x混淆)。向量积可以被定义为:
|向量a×向量b|=|a||b|sinθ在这里θ表示两向量之间的角夹角(0° ≤ θ ≤ 180°),它位于这两个矢量所定义的平面上。
这个定义有一个问题,就是同时有两个单位向量都垂直于和:若满足垂直的条件,那么也满足。
一个简单的确定满足“右手定则”的结果向量的方向的方法是这样的:若坐标系是满足右手定则的,当右手的四指从a以不超过180度的转角转向b时,竖起的大拇指指向是c的方向。
向量积|c|=|a×b|=|a| |b|sin
即c的长度在数值上等于以a,b,夹角为θ组成的平行四边形的面积。
c的方向垂直于a与b所决定的平面,c的指向按右手规则从a转向b来确定。
向量积
设
=(
),
=(
)。i,j,k分别是X,Y,Z轴方向的单位向量,则:
向量积
a×b=(
-
)i+(
-
)j+(
-
)k,为了帮助记忆,利用三阶行列式,写成det
向量积
b×a= -a×b右手规则
向量积
三角形ABC的面积=
向量积_向量积 -性质
几何意义
叉积的长度 |a×b| 可以解释成以a和b为邻边的平行四边形的面积。
混合积 [a b c] = (a×b)・c可以得到以a,b,c为棱的平行六面体的体积。
代数规则
反交换律:
a×b= -b×a
加法的分配律:
a× (b+c) =a×b+a×c
与标量乘法兼容:
(ra) ×b=a× (rb) = r(a×b)
不满足结合律,但满足雅可比恒等式:
a× (b×c) +b× (c×a) +c× (a×b) =0
分配律,线性性和雅可比恒等式别表明:具有向量加法和叉积的 R3 构成了一个李代数。
两个非零向量 a 和b 平行,当且仅当a×b=
拉格朗日公式
这是一个著名的公式,而且非常有用:
a× (b×c) =b(a・c) -c(a・b),
二重向量叉乘化简公式及证明
证明过程如下:
可以简单地记成“BAC - CAB”。这个公式在物理上简化向量运算非常有效。需要注意的是,这个公式对微分算子不成立。
这里给出一个和梯度相关的一个情形:
这是一个霍奇拉普拉斯算子的霍奇分解 的特殊情形。
另一个有用的拉格朗日恒等式是:
这是一个在四元数代数中范数乘法 | vw | = | v | | w | 的特殊情形。
矩阵形式
给定直角坐标系的单位向量i,j,k满足下列等式:
i×j=k;
j×k=i ;
k×i=j ;
通过这些规则,两个向量的叉积的坐标可以方便地计算出来,不需要考虑任何角度:设
a= [a1, a2, a3] =a1i+ a2j+ a3k
b= [b1,b2,b3]=b1i+ b2j+ b3k ;
则
a × b= [a2b3-a3b2,a3b1-a1b3, a1b2-a2b1]
上述等式可以写成矩阵的行列式的形式:
叉积也可以用四元数来表示。注意到上述 i,j,k 之间的叉积满足四元数的乘法。一般而言,若将向量 [a1, a2, a3] 表示成四元数 a1i + a2j + a3k,两个向量的叉积可以这样计算:计算两个四元数的乘积得到一个四元数,并将这个四元数的实部去掉,即为结果。更多关于四元数乘法,向量运算及其几何意义请参见四元数与空间旋转。
高维情形
七维向量的叉积可以通过八元数得到,与上述的四元数方法相同。
七维叉积具有与三维叉积相似的性质:
双线性性:
x × (ay + bz) = ax × y + bx ×z
(ay + bz) ×x = ay × x + bz × x.
反交换律:
x × y + y ×x = 0
同时与 x 和 y 垂直:
x ・ (x ×y) =y ・ (x ×y) = 0
拉格朗日恒等式
|x × y|2 = |x|2 |y|2 - (x ・y)2.
不同于三维情形,它并不满足雅可比恒等式:
x × (y × z) + y × (z × x) + z × (x ×y) ≠ 0
向量积_向量积 -向量应用
在物理学光学和计算机图形学中,叉积被用于求物体光照相关问题。
求解光照的核心在于求出物体表面法线,而叉积运算保证了只要已知物体表面的两个非平行矢量(或者不在同一直线的三个点),就可依靠叉积求得法线。
向量积_向量积 -相关介绍
向量积:在三维坐标系中,从坐标原点O沿X轴取向量OA=a,沿Y轴取向量OB=b.从原点OC垂直与OAB平面,其向量积OC=a*b,其方向由右手法则确定右手拇指指向OA,食指指向OB,中指指向OC。因此可以断定OC向量积是作用于OAB平面上的,而单一力距只垂直一轴作杠杆转动。
 爱华网
爱华网