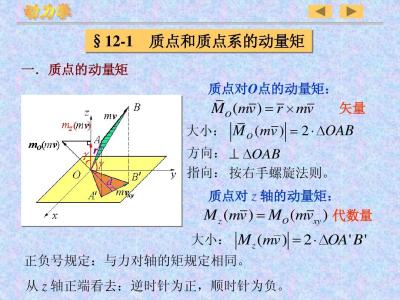
动力学普遍定理之一,它给出质点系的动量矩与质点系受机械作用的冲量矩之间的关系。动量矩定理有微分形式和积分形式两种。微分形式的动量矩定理定义质点系中第 i个质点对某定点O的动量矩为L=ri×mivi(ri为第i个质点的矢径,mivi为第i个质点的动量),它所受外力对点O的力矩为M,所受内力对点O的力矩为M。将上式的两侧对时间求导数,有。即在某一时间间隔内,刚体对z轴动量矩(Izω)的改变,等于在同一时间间隔内作用于刚体上所有外力对 z轴的冲量矩的代数和。
动量矩定理_动量矩定理 -基本简介
微分形式的动量矩定理定义质点系中第 i个质点对某定点O的动量矩为L=ri×mivi(ri为第i个质点的矢径,mivi为第i个质点的动量),它所受外力对点O的力矩为M,所受内力对点O的力矩为M。将上式的两侧对时间求导数,有。考虑所有质点的合成效果,可得: (1)
动量矩定理
式中
动量矩定理
为作用于质点系诸外力对点O的力矩的矢量和;
动量矩定理
为诸内力对点O的力矩的矢量和。但因内力具有大小相等、方向相反和共线的特点,故
动量矩定理
。同时,
动量矩定理
为质点系对点O的总动量矩,故(1)式可写作:
。(2)
式(2)就是用微分形式表示的动量矩定理,它表明:质点系对某定点 O的动量矩对时间的导数等于质点系所受诸外力对该点的力矩的矢量和。若将式 (2)两边投影到直角坐标轴上,则有:质点系对某定轴的动量矩的时间导数等于质点系上所受诸外力对相同轴的力矩的代数和。
动量矩定理
积分形式的动量矩定理 将式(2)改写成 dLO=
动量矩定理
并进行积分。若LL和L分别表示质点系在时刻t1和t2对某点O的动量矩,则
,
式中Gi为作用于质点i上的外力在时间间隔 (t2-t1)内对O点的冲量矩。式(3)就是用积分形式表示的动量矩定理,它表明:在某力学过程的时间间隔内,质点系对某点动量矩的改变,等于在同一时间间隔内作用于质点系所有外力对同一点的冲量矩的矢量和。
对刚体绕定轴z以角速度ω转动(转动惯量为Iz)的情况,可将式(3)投影到z轴上,得: ,
即在某一时间间隔内,刚体对z轴动量矩(Izω)的改变,等于在同一时间间隔内作用于刚体上所有外力对 z轴的冲量矩的代数和。
质点是质点系的一个特殊情况,故动量矩定理也适用于质点。
 爱华网
爱华网