形如y=x^a(a为常数)的函数,即以底数为自变量幂为因变量,指数为常量的函数称为幂函数。形如y=x^a(a为常数)的函数,即以底数为自变量,幂为因变量,指数为常量的函数称为幂函数。当a取非零的有理数时是比较容易理解的,而对于a取无理数时,初学者则不大容易理解了。因此,在初等函数里,我们不要求掌握指数为无理数的问题,只需接受它作为一个已知事实即可,因为这涉及到实数连续性的极为深刻的知识。
幂函数_幂函数 -概念
形如y=x^a(a为常数)的函数,即以底数为自变量,幂为因变量,指数为常量的函数称为幂函数。当a取非零的有理数时是比较容易理解的,而对于a取无理数时,初学者则不大容易理解了。因此,在初等函数里,我们不要求掌握指数为无理数的问题,只需接受它作为一个已知事实即可,因为这涉及到实数连续性的极为深刻的知识。
幂函数_幂函数 -性质
所有的幂函数在(-∞,+∞)上都有各自的定义,并且图像都过点(1,1)。
(1)当α>0时,幂函数y=xa有下列性质:
a、图像都通过点(1,1)(0,0);
b、在第一象限内,函数值随x的增大而增大;
c、在第一象限内,α>1时,图像开口向上;0<α<1时,图像开口向右;
d、函数的图像通过原点,并且在区间[0,+∞)上是增函数。
(2)当α<0时,幂函数y=xa有下列性质:
a、图像都通过点(1,1);
b、在第一象限内,函数值随x的增大而减小,图像开口向上;
c、在第一象限内,当x从右趋于原点时,图像在y轴上方趋向于原点时,图像在y轴右方无限接近y轴,当x趋于+∞时,图象在x轴上方无限地逼近x轴。
(3)当α=0时,幂函数y=xa有下列性质:
a、y=x0是直线y=1去掉一点(0,1)它的图像不是直线。
幂函数_幂函数 -特性
对于a的取值为非零有理数,有必要分成几种情况来讨论各自的特性:
首先我们知道如果a=p/q,且p/q为既约分数(即p、q互质),q和p都是整数,则x^(p/q)=q次根号下(x的p次方),如果q是奇数,函数的定义域是R,如果q是偶数,函数的定义域是[0,+∞)。当指数a是负整数时,设a=-k,则y=1/(x^k),显然x≠0,函数的定义域是(-∞,0)∪(0,+∞)。因此可以看到x所受到的限制来源于两点,一是有可能作为分母而不能是0,一是有可能在偶数次的根号下而不能为负数,那么我们就可以知道:
a小于0时,x不等于0;
a的分母为偶数时,x不小于0;
a的分母为奇数时,x取R。
幂函数_幂函数 -定义域和值域
当a为不同的数值时,幂函数的定义域的不同情况如下:
1.如果a为负数,则x肯定不能为0,不过这时函数的定义域还必须根据q的奇偶性来确定,即如果同时q为偶数,则x不能小于0,这时函数的定义域为大于0的所有实数;2.如果同时q为奇数,则函数的定义域为不等于0的所有实数。
当x为不同的数值时,幂函数的值域的不同情况如下:
1.在x大于0时,函数的值域总是大于0的实数。
2.在x小于0时,则只有同时q为奇数,函数的值域为非零的实数。
而只有a为正数,0才进入函数的值域。
由于x大于0是对a的任意取值都有意义的,
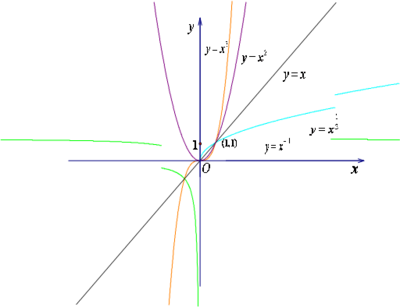
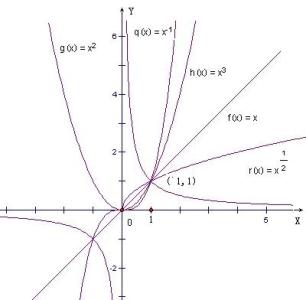
因此下面给出幂函数在第一象限的各自情况。
幂函数_幂函数 -特殊性
可以看到:
(1)所有的图形都通过(1,1)这点.(a≠0)a>0时图象过点(0,0)和(1,1)
(2)单调区间:
当a为整数时,a的正负性和奇偶性决定了函数的单调性:
①当a为正奇数时,图像在定义域为R内单调递增;
②当a为正偶数时,图像在定义域为第二象限内单调递减,在第一象限内单调递增;
③当a为负奇数时,图像在第一三象限各象限内单调递减(但不能说在定义域R内单调递减);
④当a为负偶数时,图像在第二象限上单调递增,在第一象限内单调递减。
当a为分数时,a的正负性和分母的奇偶性决定了函数的单调性:
①当a>0,分母为偶数时,函数在第一象限内单调递增;
②当a>0,分母为奇数时,函数在第一三象限各象限内单调递增;
③当a<0,分母为偶数时,函数在第一象限内单调递减;
④当a<0,分母为奇数时,函数在第一三象限各象限内单调递减(但不能说在定义域R内单调递减);
(3)当a>1时,
幂函数图形下凸(竖抛);当0<a<1时,幂函数图形上凸(横抛)。当a<0时,图像为双曲线。
(4)在(0,1)上,幂函数中a越大,函数图像越靠近x轴;在(1,
 爱华网
爱华网