正四面体是由四个全等正三角形围成的空间封闭图形,所有棱长都相等。它有4个面,6条棱,4个顶点。正四面体是最简单的正多面体,同时也是一种特殊的正三棱锥。正四面体得基本性质主要有:这是一种柏拉图多面体,正四面体与自身对偶。有一个在其内部的内切球和七个与四个面都相切的旁切球,其中有三个旁切球球心在无穷远处。与正八面体填满空间,在一个顶点周围有八个正四面体和六个正八面体,对边相互垂直。正四面体键角是109度28分,约为109.47°。正四面体可与正八面体填满空间,在一顶点周围有八个正四面体和六个正八面体。
正四面体_正四面体 -概念简介
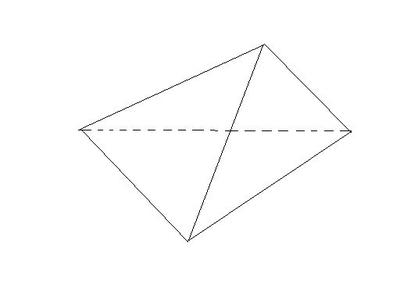
示意图正四面体是由四个等边三角形组成的正多面体,是一种锥体,有4个顶点,6条边和4个正三角形面。
将立方体的其中四个顶点两两相连,而这四个顶点任何两条都没有落在立方体同一条的边上,可得到一个正四面体,其边长为立方体边长的√2,其体积为立方体体积的1/3,从这里看,正四面体是半立方体。正四面体是一个拥有无穷多个成员的多胞形家族―正单纯形家族的3维成员。正四面体是一种棱锥体,即它可以被描述成由一个多边形底面和链接底面和一个共同顶点的三角形面组成,对于正四面体来说,这个底面是正三角形,并且它的侧面也都是正三角形,应此正四面体是正三棱锥。
正四面体是三维的正单纯形(3-simplex),这意味着四面体是三维中最简单的多面体,顶点数、棱数、面数比它少的多面体都只能成为退化多面体,同时在更高维的超空间中,任意4个顶点一定共在同一三维空间中,这4个顶点若不存在四点共面、三点共线和两点重合的情况,一定能构成一个四面体,并且只要6条棱的长度确定了,四面体就被唯一确定了(即四面体具有稳定性。这是单纯形面多胞形共有的一个基本特性),由此可知,一个四面体的6条棱长都相等,则其一定是一个正四面体。正四面体是柏拉图立体中唯一一个所有顶点之间的距离都相等的,同时正四面体也是三维空间中使4个顶点每两个顶点间距离相等的唯一方式。
定义
正四面体是由四个全等正三角形围成的空间封闭图形,所有棱长都相等。
它有4个面,6条棱,4个顶点。正四面体是最简单的正多面体。
正四面体_正四面体 -正三棱锥
正四面体属于正三棱锥,但是正三棱锥只需要底面为正三角形,其他三个面是全等的等腰三角形就可以,不需要四个面全等且都是等边三角形。
因此,正四面体又是特殊的正三棱锥。
正四面体_正四面体 -基本性质
正四面体是一种柏拉图多面体,正四面体与自身对偶。
正四面体的重心、四条高的交点、外接球、内切球球心共点,此点称为中心。
正四面体有一个在其内部的内切球和七个与四个面都相切的旁切球,其中有三个旁切球球心在无穷远处。
正四面体有四条三重旋转对称轴,六个对称面。
正四面体可与正八面体填满空间,在一顶点周围有八个正四面体和六个正八面体。
正四面体的对边相互垂直。
化学中CH4,CCl4,SiH4等物质也是正四面体结构。
正四面体键角是109度28分,约为109.47°。
正四面体_正四面体 -相关数据
当正四面体的棱长为a时,一些数据如下:
高:√6a/3。中心把高分为1:3两部分。
表面积:√3a^2
体积:√2a^3/12
对棱中点的连线段的长:√2a/2
外接球半径:√6a/4,正四面体体积占外接球体积的2*3^0.5/9*π,约12.2517532%。
内切球半径:√6a/12,内切球体积占正四面体体积的π*3^0.5/18,约30.2299894%。
棱切球半径:√2a/4.
两条高夹角:2ArcSin(√6/3)=ArcCos(-1/3)=≈1.910633236249(弧度)或109°28′16″3942841664889。这一数值与三维空间中求最小面有关,也是蜂巢底菱形的钝角的角度.
两邻面夹角:2ArcSin(√3/3)=ArcCos(1/3)≈1.23095(弧度)或70°31′43″60571,与两条高夹角在数值上互补。
侧棱与底面的夹角:ArcCos(√3/3)
正四面体的对棱相等。具有该性质的四面体符合以下条件:
1.四面体为对棱相等的四面体当且仅当四面体每对对棱的中点的连线垂直于这两条棱。
2.四面体为对棱相等的四面体当且仅当四面体每对对棱中点的三条连线相互垂直。
3.四面体为对棱相等的四面体当且仅当四条中线相等。
正四面体_正四面体 -建系方法
示意图1.设有一正四面体D-ABC棱长为a
以AB边为y轴A为顶点ABC所属平面为xOy面建系
四个顶点的坐标依次为
 爱华网
爱华网