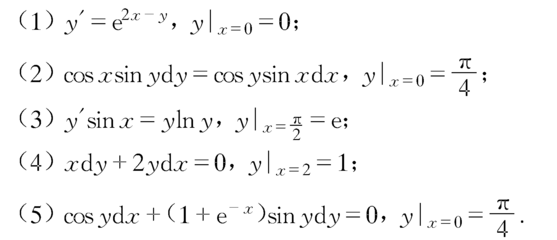一阶线性微分方程,形如y'+P(x)y=Q(x)的微分方程称为一阶线性微分方程,Q(x)称为自由项。形如y'+P(x)y=Q(x)的微分方程称为一阶线性微分方程,Q(x)称为自由项。详细解释:一阶,指的是方程中关于Y的导数是一阶导数。线性,指的是方程的每一项关于y、y'的次数相等。
一阶线性微分方程_一阶线性微分方程 -定义

一阶线性微分方程形如y'+P(x)y=Q(x)的微分方程称为一阶线性微分方程,Q(x)称为自由项。
详细解释:一阶,指的是方程中关于Y的导数是一阶导数。
线性,指的是方程的每一项关于y、y'的次数相等。
一阶线性微分方程_一阶线性微分方程 -分类
一阶线性微分方程当Q(x)≡0时,方程为y'+P(x)y=0,这时称方程为一阶齐次线性微分方程。(因为y'是关于y及其各阶导数的0次的,P(x)y是一次项,它们同时又是关于x及其各阶导数的0次项,所以为齐次。)当Q(x)≠0时,称方程y'+P(x)y=Q(x)为一阶非齐次线性微分方程。(由于Q(x)中未含y及其导数,所以是关于y及其各阶导数的0次项,因为方程中含一次项又含0次项,所以为非齐次。)
一阶线性微分方程_一阶线性微分方程 -解法
一阶线性微分方程一阶线性微分方程的求解一般采用常数变易法,通过常数变易法,可求出一阶线性微分方程的通解。
一阶齐次线性微分方程的通解对于一阶齐次线性微分方程:
其通解形式为:
一阶线性微分方程其中C为常数,由函数的初始条件决定
一阶非齐次线性微分方程的通解
对于一阶齐次线性微分方程:其通解形式为:
其中C为常数,由函数的初始条件决定
 爱华网
爱华网