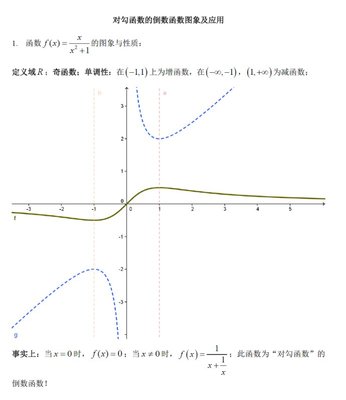
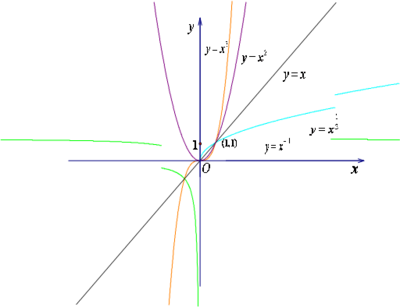
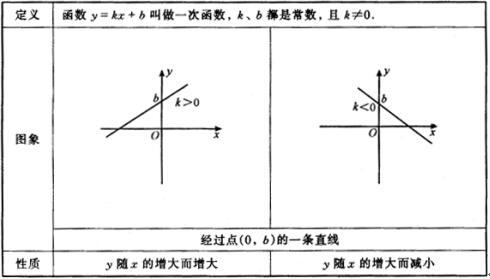
一般地,两个变量x、y之间的关系式可以表示成形如y=kx的函数(k为常数,x的次数为1,且k≠0)(简称f(x)),那么y就叫做x的正比例函数。正比例函数属于一次函数,但一次函数却不一定是正比例函数。正比例函数是一次函数的特殊形式,即一次函数y=kx+b中,若b=0,即所谓“y轴上的截距”为零,则为正比例函数。正比例函数的关系式表示为:y=kx(k为比例系数)当K>0时(一三象限),K的绝对值越大,图像与y轴的距离越近。函数值y随着自变量x的增大而增大。当K<0时(二四象限),k的绝对值越小,图像与y轴的距离越远。自变量x的值增大时,y的值则逐渐减小。
正比例函数_正比例函数 -概念
正比例函数正比例函数是函数的一种,也是一种关系,这种关系使一个集合里的每一个元素对应到另一个(可能相同的)集合里的唯一元素。正比例函数关系是满足一定条件的一种关系。
一般地,两个变量x,y之间的关系式可以表示成形如y=kx(k为常数,且k≠0)的函数,那么y就叫做x的正比例函数。
正比例函数属于一次函数,是一次函数的特殊形式,即一次函数 y=kx+ b 中,若b=0,则为正比例函数。
正比例函数_正比例函数 -性质
1、定义域:实数集R。
2、值域:实数集R。
3、奇偶性:奇函数。
4、单调性:当k>0时,图象位于第一、三象限,y随x的增大而增大(单调递增);当k<0时,图象位于第二、四象限,y随x的增大而减小(单调递减)。
5、周期性:不是周期函数。
正比例函数_正比例函数 -解析式
设该正比例函数的解析式为 y=kx(k≠0),将已知点的坐标带入上式得到k,即可求出正比例函数的解析式。另外,若求正比例函数与其它函数的交点坐标,则将两个已知的函数解析式联立成方程组,求出其x,y值即可。
正比例函数_正比例函数 -图像
正比例函数的图像是经过坐标原点(0,0)和定点(x,kx)两点的一条直线,它的斜率是k,横、纵截距都为0。
正比例函数_正比例函数 -图像作法
1、列表
2、描点
3、连线(一定要经过坐标轴的原点)
正比例函数_正比例函数 -联系与区别
正比例表示的是两个量的商是一定值,说明两个量成正比,但不能说明y与X成正比例函数。正比例函数_正比例函数 -应用
正比例函数在线性规划问题中体现的力量也是无穷的。比如斜率问题就取决于K值,当K越大,则该函数图像与x轴的夹角越大,反之亦然。还有,y=kx 是 y=k/x 的图像的对称轴。
①正比例:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做成正比例关系. ①用字母表示:如果用字母x和y表示两种相关联的量,用k表示它们的比值,(一定)正比例关系可以用以下关系式表示:
②正比例关系两种相关联的量的变化规律:对于比值为正数的,即y=kx(k>0),此时的y与x,同时扩大,同时缩小,比值不变.例如:汽车每小时行驶的速度一定,所行的路程和所用的时间是否成正比例?
以上各种商都是一定的,那么被除数和除数. 所表示的两种相关联的量,成正比例关系. 注意:在判断两种相关联的量是否成正比例时应注意这两种相关联的量,虽然也是一种量,随着另一种的变化而变化,但它们相对应的两个数的比值不一定,它们就不能成正比例. 例如:一个人的年龄和它的体重,就不能成正比例关系,正方形的边长和它的面积也不成正比例关系。
正比例函数_正比例函数 -解析式求法
1、已知一点坐标,用待定系数法求函数解析式。先设解析式为y=kx,再代入已知点坐标,解出k的值。
2、在应用题中,可以根据条件直接写出解析式。先找出自变量x和因变量y,找出两者的等量关系即可列出函数解析式。
正比例函数_正比例函数 -图像作法
1、在x允许的范围内取一个值,根据解析式求出y的值;
2、根据第一步求的x、y的值描出点;
3、作出第二步描出的点和原点的直线(因为两点确定一直线)。
正比例函数_正比例函数 -应用
正比例函数在线性规划问题中体现的力量也是无穷的。
比如斜率问题就取决于k值,当k越大,则该函数图像与x轴的夹角越大,反之亦然。
还有,y=kx是y=k/x的图像的对称轴。
①正比例:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做成正比例关系。
②用字母表示:如果用字母x和y表示两种相关联的量,用k表示它们的比值,(一定)正比例关系可以用以下关系式表示:
③正比例关系两种相关联的量的变化规律:对于比值为正数的,即y=kx(K为常数,k≠0),此时的y与x,同时扩大,同时缩小,比值不变。例如:汽车每小时行驶的速度一定,所行的路程和所用的时间成正比例.以上各种商都是一定的,那么被除数和除数所表示的两种相关联的量成正比例关系。注意:在判断两种相关联的量是否成正比例时,应注意这两种相关联的量,虽然也是一种量随着另一种的变化而变化,但它们相对应的两个数的比值不一定,那它们就不能成正比例。例如:一个人的年龄和它的体重,就不能成正比例关系,正方形的边长和它的面积也不成正比例关系。而单价数量与总价是成正比的(单价不变,总价随着数量的增减而增减)
正比例函数_正比例函数 -例题
首先通过5个问题,得出5个函数,观察这5个函数,可纳出正比例函数概念。要能判断一个函数是否为正比例函数。然后画出4个正比例函数图象,观察归纳出正比例函数的性质。重点就是正比例函数概念及正比例函数的性质。
根据上面的5个实际问题,我们得到5个函数。下面观察这5个函数的共同点,以便归纳出正比例函数概念。
①h=2t;②m=7.8n;③s=0.5t;④T=t/3;⑤y=200x。
这5个函数有什么共同的特点?
1:都有自变量。
2:都是函数。
3:都有常量。
这5个函数的右边都是常量和自变量的什么形式?
这5个函数都是常量与自变量的乘积形式,都可表达为y=kx(k不等于0)的形式。
下面是4个函数,请判断哪些是正比例函数?
①y=3;②y=2x;③y=1/x;④y=x^2。
解答:
②是正比例函数。因为它符合正比例函数的的定义。①,③,④则不是正比例函数。①:它为常数函数,无自变量。③:它为反比例函数。④:它为二次函数。
习题
已知y-2与x成正比例,且当x=1时y=-6.
(1)求y与x之间的函数关系式;
(2)若点(a,-20)在这个函数关系式上,求a.
 爱华网
爱华网