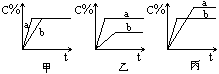化学平衡是指在宏观条件一定的可逆反应中,化学反应正逆反应速率相等,反应物和生成物各组分浓度不再改变的状态。可用ΔrGm=ΣνΑμΑ=0判断,μA是反应中A物质的化学式。根据勒夏特列原理,如一个已达平衡的系统被改变,该系统会随之改变来抗衡该改变。影响化学平衡移动的因素主要有浓度、温度、压强等。通常说的四大化学平衡为氧化还原平衡、沉淀溶解平衡、配位平衡、酸碱平衡。关于气体的化学平衡有这两种基本模型,即一种是等容装置,另一种是等压装置。
化学平衡_化学平衡 -平衡常数
可逆反应达到化学平衡
平衡常数
可逆反应达到化学平衡化学平衡常数,是指在一定温度下,可逆反应无论从正反应开始,还是从逆反应开始,也不管反应物起始浓度大小,最后都达到平衡,这时各生成物浓度的化学计量数次幂的乘积除以各反应物浓度的化学计量数次幂的乘积所得的比值是个常数,用K表示,这个常数叫化学平衡常数。
反应aA(g)+bB(g)=cC(g)+dD(g)
K=(C浓度的c次方乘D浓度的d次方)除以(A浓度的a次方乘B浓度的b次方)
关于平衡常数的计算与图像分析
典例:某恒温密闭容器发生可逆反应Z(?)+W(?)=(可逆)X(g)+Y(?);ΔH,在t1时刻反应达到平衡,在t2时刻缩小容器体积,t3时刻再次达到平衡状态后未再改变条件。下列有关说法中不正确的是(B)
A.Z和W在该条件下一定不为气态
B.t1~t2时间段与t3时刻后,两时间段反应体系中气体的平均摩尔质量不可能相等
C.若在该温度下此反应平衡常数表达式为K=c(X),则t1~t2时间段与t3时刻后的X浓度相等
D.若该反应只在某温度T0以上自发进行,则该反应的平衡常数K随温度升高而增大
化学平衡_化学平衡 -平衡移动
在化学反应条件下,因反应条件的改变,使可逆反应从一种平衡状态转变为另一种平衡状态的过程,叫化学平衡的移动。化学平衡发生移动的根本原因是正逆反应速率不相等,而平衡移动的结果是可逆反应到达了一个新的平衡状态,此时正逆反应速率重新相等(与原来的速率可能相等也可能不相等)。
影响化学平衡移动的因素主要有浓度.温度.压强等。
浓度对化学平衡移动的影响
在其他条件不变时,增大反应物的浓度或减小生成物的浓度,有利于正反应的进行,平衡向右移动;增加生成物的浓度或减小反应物的浓度,有利于逆反应的进行平衡向左移动。单一物质的浓度改变只是改变正反应或逆反应中一个反应的反应速率而导致正逆反应速率不相等,而导致平衡被打破。
压强对化学平衡移动的影响
对于气体反应物和气体生成物分子数不等的可逆反应来说,当其它条件不变时,增大总压强,平衡向气体分子数减少即气体体积缩小的方向移动;减小总压强,平衡向气体分子数增加即气体体积增大的方向移动。若反应前后气体总分子数(总体积)不变,则改变压强不会造成平衡的移动。压强改变通常会同时改变正逆反应速率,对于气体总体积较大的方向影响较大,例如,正反应参与的气体为3体积,逆反应参与的气体为2体积,则增大压强时正反应速率提高得更多,从而是v正>v逆,即平衡向正反应方向移动;而减小压强时,则正反应速率减小得更多,平衡向逆反应方向移动。
温度对化学平衡移动的影响
在其他条件不变时,升高反应温度,有利于吸热反应,平衡向吸热反应方向移动;降低反应温度,有利于放热反应,平衡向放热反应方向移动。与压强类似,温度的改变也是同时改变正逆反应速率,升温总是使正逆反应速率同时提高,降温总是使正逆反应速率同时下降。对于吸热反应来说,升温时正反应速率提高得更多,而造成v正>v逆的结果;降温时吸热方向的反应速率下降得也越多。与压强改变不同的是,每个化学反应都会存在一定的热效应,所以改变温度一定会使平衡移动,不会出现不移动的情况。
化学平衡_化学平衡 -研究历史
19世纪50-60年代,热力学的基本规律已明确起来,但是一些热力学概念还比较模糊,数字处理很烦琐,不能用来解决稍微复杂一点的问题,例如化学反应的方向问题。当时,大多数化学家正致力于有机化学的研究,也有一些人试图解决化学反应的方向问题。这种努力除了质量作用定律之外,还有其他一些人试图从别的角度进行反应方向的探索,其中已有人提出了一些经验性的规律。
在这一时期,丹麦人汤姆生和贝特罗试图从化学反应的热效应来解释化学反应的方向性。他们认为,反应热是反应物化学亲合力的量度,每个简单或复杂的纯化学性的作用,都伴随着热量的产生。贝特罗更为明确地阐述了与这相同的观点,并称之为“最大功原理”,他认为任何一种无外部能量影响的纯化学变化,向着产生释放出最大能量的物质的方向进行。虽然这时他发现了一些吸热反应也可以自发地进行,但他却主观地假定其中伴有放热的物理过程。这一错误的论断在30年代终于被他承认了,这时他才将“最大功原理”的应用范围限制在固体间的反应上,并提出了实际上是“自由焓”的化学热的概念。
19世纪60-80年代,霍斯特曼、勒夏特列和范霍夫在这一方面也做了一定的贡献。首先,霍斯特曼在研究氯化铵的升华过程中发现,在热分解反应中,其分解压力和温度有一定的关系,符合克劳胥斯一克拉佩隆方程:dp/dt=Q/T(V'-V)
其中Q代表分解热,V、V'代表分解前后的总体积。范霍夫依据上述方程式导出的下式:
lnK=-(Q/RT)+c
此式可应用于任何反应过程,其中Q代表体系的吸收的热(即升华热)。范霍夫称上式为动态平衡原理,并对它加以解释,他说,在物质的两种不同状态之间的任何平衡,因温度下降,向着产生热量的两个体系的平衡方向移动。1874年和1879年,穆迪埃和罗宾也分别提出了这样的原理。穆迪埃提出,压力的增加,有利于体积相应减少的反应发生。在这之后,勒夏特列又进一步普遍地阐释了这一原理。他说,处于化学平衡中的任何体系,由于平衡中的多个因素中的一个因素的变动,在一个方向上会导致一种转化,如果这种转化是惟一的,那么将会引起一种和该因素变动符号相反的变化。
然而,在这一方面做出突出贡献的是吉布斯,他在热力化学发展史上的地位极其重要。吉布斯在势力化学上的贡献可以归纳4个方面。第一,在克劳胥斯等人建立的第二定律的基础上,吉布斯引出了平衡的判断依据,并将熵的判断依据正确地限制在孤立体系的范围内。使一般实际问题有了进行普遍处理的可能。第二,用内能、熵、体积代替温度、压力、体积作为变量对体系状态进行描述。并指出汤姆生用温度、压力和体积对体系体状态进行描述是不完全的。他倡导了当时的科学家们不熟悉的状态方程,并且在内能、熵和体积的三维坐标图中,给出了完全描述体系全部热力学性质的曲面。第三,吉布斯在热力学中引入了“浓度”这一变量,并将明确了成分的浓度对内能的导数定义为“热力学势”。这样,就使热力学可用于处理多组分的多相体系,化学平衡的问题也就有了处理的条件。第四,他进一步讨论了体系在电、磁和表面的影响下的平衡问题。并且,他导出了被认是热力学中最简单、最本质也是最抽象的热力学关系,即相律,在,而平衡状态就是相律所表明的自由度为零的那种状态。
吉布斯对平衡的研究成果主要发表在他的三篇文章之中。1873年,他先后将前两篇发表在康涅狄格州学院的学报上,立即引起了麦克斯韦的注意。吉布斯前两篇文可以说只是一个准备,1876年和1878年分两部分发表了第三篇文章-《关于复相物质的平衡》,文章长达300多页,包括700多个公式。前两篇文章是讨论单一的化学物质体系,这篇文章则对多组分复相体系进行了讨论。由于热力学势的引入,只要将单组分体系状态方程稍加变化,便可以对多组分体系的问题进行处理了。
对于吉布斯的工作,勒夏特列认为这是一个新领域的开辟,其重要性可以与质量不灭定律相提并论。然而,吉布斯的三篇文章发表之后,其重大意义并未被多数科学家们所认识到,直到1891年才被奥斯特瓦德译成德文,1899年勒夏特列译成法文出版之后,情况顿然改变。在吉布斯之后,热力学仍然只能处理理想状态的体系。这时,美国人洛易斯分别于1901年和1907年发表文章,提出了“逸度”与“活度”的概念。路易斯谈到“逃逸趋势”这一概念,指出一些热力学量,如温度、压力、浓度、热力学势等都是逃逸趋势量度的标度。
路易斯所提出的逸度与活度的概念,使吉布斯的理论得到了有益的补充和发展,从而使人们有可能将理想体系的偏差进行统一,使实际体系在形式上具有了与理想体系完全相同的热力学关系式。
综上所述,化学平衡状态是指在一定条件下的可逆反应,正反应和逆反应的速率相等,反应混合物中各组分的浓度保持不变的状态。
化学平衡_化学平衡 -基本模型
关于气体的化学平衡有这两种基本模型,即一种是等容装置,另一种是等压装置。
化学平衡_化学平衡 -具体解释
对于一个反应Ma+Nb=Qc+Dp其中M,N,Q,D为方程式前的计量数。
第一大类;TV不变,即容积不变时
1.M+N>Q+D或M+N
这个时候只能建立等同平衡,记住这时只能建立等同。
什么叫等同?顾名思义,就是什么都是相同的。
这个相同是建立在平衡的基础上的,平衡是不管你怎么加都是那个百分含量。
2.M+N=Q+D的时候
这个时候可以建立等效平衡
即在平衡时候之前加入的个生成物是按比例生成的
这个时候的各物质浓度会随着加入的比的变化而变化
但这两种情况各物质的百分含量是不变的
其实等效平衡你可以理解为平衡时各物质的关系是相同的
第二大类:TP不变即容器的压强不变
这类的容器一般与活塞相连】
保证了活塞内气体的作用力不变。
还是这两类
1.M+N>Q+D或M+N
这种类型的可逆反应。由于压强是会随着反应的改变而改变的,但在这种容器中外界的大气压力会使反应时刻处于平衡状态。故这种平衡下什么都是不变的
如
各物质的浓度百分比
2.M+N=Q+D
这种类型的可以说是以上所有类型的综合体。就是真正意义上的什么都不变。他的意义就好像是你进行同一个反应,一个用大碗一个用小碗一样。
化学平衡_化学平衡 -等效平衡
1.等效平衡
(1)定义
同一可逆反应,一定条件下,当改变起始时反应物或生成物物质的量或物质的量浓度,达到平衡时,混合物中各组分的百分组成相等,这样的平衡称等效平衡。
(2)产生原因
平衡,只与温度、压强和浓度有关,与加料顺序无关。
根据气体状态方程,pV=nRT,可以发现:如果保持温度不变,恒容体系,只要“一边倒”之后,各组分n相同,压强也相同,平衡状态也相同。如果保持温度不变,恒压体系,只要“一边倒”之后,各组分n成同一比例,浓度也相同,那么平衡状态也相同。
2.规律与判断
(1) 一般可逆反应,恒温恒容时,当起始反应物或生成物的物质的量通过化学计量数换算相同时,则建立等效平衡。
如反应 2SO?+O?=(可逆)=2SO? 在(A)、(B)条件时建立等效平衡
(A) 起始时加入:2mol SO? + 1mol O?
(B) 起始时加入:2mol SO?
注意:此情况下,无论反应物还是生成物,起始时物质的量一定要与化学计量数比相同。
(2) 一般可逆反应,恒温恒压时,当起始反应物或生成物的物质的量比(不一定要求与化学计量数比相同)相同时,即建立等效平衡。
如反应 2SO?+O?=(可逆)=2SO? 在(C)、(D)时建立等效平衡
(C)起始时加入:1mol SO? + 1mol O?
(D)起始时加入:2mol SO? + 2mol O?
(3) 对于反应前后体积不变的气体反应,恒温恒容时,当起始反应物或者生成物的物质的量比(不一定要求与化学计量数比相同)相同时,建立等效平衡。
如反应 H?+I?(气) 2HI 在(E)、(F)时建立等效平衡
(E)起始时加入:1mol H?+2mol I?
(F)起始时加入:2mol H?+4mol I?
3.应用
利用等效平衡原理进行平衡问题分析2例
例1在相同条件下(T=500K),相同体积的甲乙两容器,甲中充入1mol SO?和1mol O?,乙中充入2mol SO?和2mol O?,下列叙述中不正确的是( )
(A) 反应速率:乙>甲 (B) 平衡混合物中SO?的体积分数:乙>甲
(B)SO?的转化率:乙>甲 (D) 平衡时O?的体积分数:甲>乙
简析
若将乙容器的容积扩大2倍,则甲乙为等效平衡;再将乙容器容积恢复到原体积,则压强增大,反应速率增大,平衡向生成SO?的方向移动,故(A)、(C)、(D)项都是正确的,只有(B)项是错误的。答案(B)。
例2在一定温度下,将a molPCl?通入一容积不变的密闭容器中,达到如下平衡: PCl?(g)=(可逆)=PCl?(g)+Cl?(g) 测得平衡混合气的压强为P? ;此时,再向此反应器中通入a mol PCl?,在温度不变时,重新达到平衡时,测得压强为P?,则P? 与P? 的关系是( )
(A)2P?>P? (B) 2P?
P?
简析
第二次平衡,可以这样设计:将容器体积扩大1倍,通入2a mol PCl?,此时建立的平衡与第一次平衡相同,压强相等;再将容器体积恢复为原容积,压强增大,平衡向逆反应方向移动,混合气总物质的量减小,建立新平衡,即第二次平衡,故 P?
应用等效平衡原理分析有关化学平衡问题的一般思路:
根据已知条件,先合理变换条件,使之成为等效平衡;然后将体系恢复为原条件,再恢复原条件。
关于等效平衡难点――推“隔板”问题
化学平衡
例:在一个容积固定的反应容器中, 有一可以左右滑动的密封隔板, 两侧分别进行如下图所示的可逆反应:
各物质的起始加入量如下: A、B、C 均为 4.0 mol, D为 6.5 mol, F为 2 mol, 设E 为 x mol, 当x 在一定范围内变化时, 均可以通过调节反应器的温度时两侧反应都达到平衡, 且隔板恰好处于反应器的正中位置。
当x = 4.5时, 则右侧反应起始时向 正反应,要使起始反应维持向该方向进行, x 的最大值应小于7。

若x 分别为 4.5 和 5.0, 则在这两种情况下, 当反应达到平衡时, A的物质的量两种情况下不相同,因为温度不同。
x = 3.0时, 右侧反应在起始时向逆反应, 要使起始反应维持向该方向进行, x 的最小值应大于2.5
x = 4.5时, 左右两侧反应体系达到平衡后, 向左侧反应器中充入a mol A气体, 当左右两侧再次达到平衡状态时, 则a 的取值范围为0
等效平衡新题型――等效热问题
例:已知:① H2(g)+N2(g)+3O2(g) =2HNO3(l);△H1= ―348.2KJ/mol,②2NO(g)= N2(g)+ O2(g);△H2= ―180.5 KJ/mol,③3NO2(g)= N2(g)+3O2(g); △H3= ―99.6 KJ/mol ④H2O(l)= H2(g)+ O2(g);△H4= +285.84 KJ/mol,⑤H2O(l)= H2O(g);△H5= +44.02 KJ/mol,⑥3NO2(g) +H2O(g)=(可逆)2HNO3(l)+ NO(g);△H6 。在一恒温恒压的密闭容器中充入5mol NO2和8mol H2O(g),记为平衡Ⅰ,达平衡时生成1molNO。相同条件下同一容器中充入xmol NO2,ymol H2O(g)和3molNO,记为平衡Ⅱ,达平衡时,NO的质量分数与平衡Ⅰ相同,且放出热量115.73KJ,则x=11,y=29。
简析:△H6= ―115.73KJ/mol,算出在平衡Ⅰ平衡时放出热量115.73KJ,平衡时剩余NO2:2 mol,H2O(g):7 mol,NO:1 mol。因为平衡Ⅱ与平衡Ⅰ等效,且放出热量相同,又因为有3molNO充入,所以需要NO2:2*3=6 mol,H2O(g):7*3=21 mol维持平衡状态,再充入与平衡Ⅰ完全相同的NO2、H2O(g)则就与原平衡放出热相同且等效,所以x=6+5=11 mol,y=21+8=29 mol,这是如今出现的较难的等效平衡问题,一旦与热联系起来就不好建立理想模型了,本题的思考方法值得借鉴。
化学平衡_化学平衡 -限度判断
1.体系中各组分的物质的量的浓度或体积分数、物质的量分数保持不变;
2.全是气体参加的、前后化学计量数改变的可逆反应,压强保持不变;
3.全是气体参加的、前后化学计量数改变的可逆反应,平均相对分子质量保持不变;
4.对于有颜色的物质参加或生成的可逆反应,颜色不随时间发生变化;
5.对同一物质而言,断裂化学键的物质的量与形成化学键的物质的量相等。
6.V正=V逆
 爱华网
爱华网