自适应及模糊信模糊神经网络(Fuzzy network-FNN)就是模糊理论同神经网络相结合的产物,它汇集了神经网络与模糊理论的优点,集学习、联想、识别、信息处理于一体。
模糊神经网络_模糊神经网络 -模糊神经网络发展动向
模糊理论和神经网络技术是近几年来人工智能研究较为活跃的两个领域。人工神经网络是模拟人脑结构的思维功能,具有较强的自学习和联想功能,人工干预少,精度较高,对专家知识的利用也较好。但缺点是它不能处理和描述模糊信息,不能很好利用已有的经验知识,特别是学习及问题的求解具有黑箱的特性,其工作不具有可解释性,同时它对样本的要求较高;模糊系统相对于神经网络而言,具有推理过程容易理解、专家知识利用较好、对样本的要求较低等优点,但它同时又存在人工干预多、推理速度慢、精度较低等缺点,很难实现自适应学习的功能,而且如何自动生成和调整隶属度函数和模糊规则,是一个棘手的问题。如果将二者有机地结合起来,可起到互补的效果。模糊神经网络_模糊神经网络 -模糊神经网络形式
模糊神经网络有如下三种形式:1.逻辑模糊神经网络
2.算术模糊神经网络
3.混合模糊神经网络
模糊神经网络就是具有模糊权系数或者输入信号是模糊量的神经网络。上面三种形式的模糊神经网络中所执行的运算方法不同。
模糊神经网络无论作为逼近器,还是模式存储器,都是需要学习和优化权系数的。学习算法是模糊神经网络优化权系数的关键。对于逻辑模糊神经网络,可采用基于误差的学习算法,也即是监视学习算法。对于算术模糊神经网络,则有模糊BP算法,遗传算法等。对于混合模糊神经网络,目前尚未有合理的算法;不过,混合模糊神经网络一般是用于计算而不是用于学习的,它不必一定学习。
模糊神经网络_模糊神经网络 -模糊神经网络用途
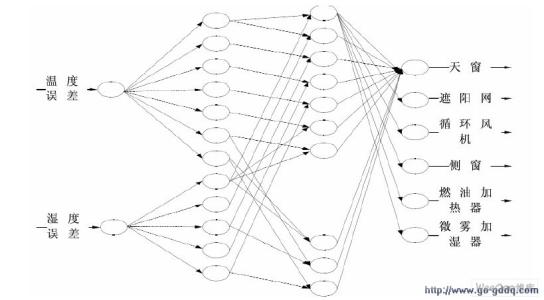
模糊神经网络可用于模糊回归、模糊控制器、模糊专家系统、模糊谱系分析、模糊矩阵方程、通用逼近器。
在控制领域中,所关心的是由模糊神经网络构成的模糊控制器。在这一章中.介绍模糊神经网络的基本结构、遗传算法、模糊神经网络的学习算法,以及模糊神经网络的应用
模糊神经网络_模糊神经网络 -摘要
模糊神经网络结合了神经网络系统和模糊系统的长处,它在处理非线性、模糊性等问题上有很大的优越性,在智能信息处理方面存在巨大的潜力;使得越来越多的专家学者投入到这个领域中来,并做出了卓有成效的研究成果。但是,对模糊神经网络的研究,大都是基于算法的创新、改进和完善,少有综述性的文献对它进行概述,使初接触这一领域的人往往无所适从,很难在短时间内理解模糊神经网络的概念,也很难实际应用它。作者在阅读了大量文献的基础上,对各种相关理论知识进行整理、归纳和研究,旨在对模糊神经网络做一个系统的概述和一些初步的探索。本文实际上由两部分组成:第一部分是对模糊神经网络的概述;第二部分是一种算法的提出及其实观过程。模糊神经网络是一个较新的概念,文章从神经网络系统与模糊系统的历史论述到它的起源与发展,论证了它产生的可能性与必要性,并简要介绍了国内外模糊逻辑神经网络软件硬件。在模糊神经元概念的基础上,定义了模糊神经网络;从函数映射角度上,讨论了神经网络系统和模糊系统的函数逼近能力;二者都能以任意精度逼近任何连续实函数;对理论成熟的算法和模型,作了简洁的介绍。针对模糊神经网终实观时的具体问题,对网终的学习能力、容量、结构分布等细节逆行了探讨。本文提出了一种模糊神经网络的二步混合算法:第一步,采用模糊推理系统结合遗传算法根据训练样本确定隶属函数的参数,通过遗传算法搜索定义域范围内的参数最优解。文中选用S-T模型作为模糊推理系统中的推理模型。第二步,确定网络结构,根据训练样本采用BP算法训练网络,调整网络权值和偏差,为了避免局部最小观象和加快网络收敛速度,选用加动量因子变学习率的改进BP算法为训练算法。为了更广泛地应用遗传算法,文中用C++,实现了通用遗传算法类库,在实观过程中结合使用了类模板,抽象类等技术。该类库支持一维和多维函数的最优化。对多维函数可以采用统一长度的或者各维长度不同的基因;支持固定和可变变异率,支持固定迭代代数结束迭代和满足一定条件结束迭代。作者用MATLAB的Fuzzy Toolbox及NNetToolbox实现了算法,仿真结果表明,该算法效率高、收敛速度快、模型精度高 爱华网
爱华网