logistic回归又称logistic回归分析,主要在流行病学中应用较多,比较常用的情形是探索某疾病的危险因素,根据危险因素预测某疾病发生的概率,等等。例如,想探讨胃癌发生的危险因素,可以选择两组人群,一组是胃癌组,一组是非胃癌组,两组人群肯定有不同的体征和生活方式等。这里的因变量就是是否胃癌,即“是”或“否”,为两分类变量,自变量就可以包括很多了,例如年龄、性别、饮食习惯、幽门螺杆菌感染等。自变量既可以是连续的,也可以是分类的。通过logistic回归分析,就可以大致了解到底哪些因素是胃癌的危险因素。
logistic模型_Logistic模型 -简介
logistic回归又称logistic回归分析,主要在流行病学中应用较多,比较常用的情形是探索某疾病的危险因素,根据危险因素预测某疾病发生的概率,等等。
概念
logistic回归又称logistic回归分析,主要在流行病学中应用较多,比较常用的情形是探索某疾病的危险因素,根据危险因素预测某疾病发生的概率,等等。例如,想探讨胃癌发生的危险因素,可以选择两组人群,一组是胃癌组,一组是非胃癌组,两组人群肯定有不同的体征和生活方式等。这里的因变量就是是否胃癌,即“是”或“否”,为两分类变量,自变量就可以包括很多了,例如年龄、性别、饮食习惯、幽门螺杆菌感染等。自变量既可以是连续的,也可以是分类的。通过logistic回归分析,就可以大致了解到底哪些因素是胃癌的危险因素。Logistic模型是种群生态学的核心理论之一。
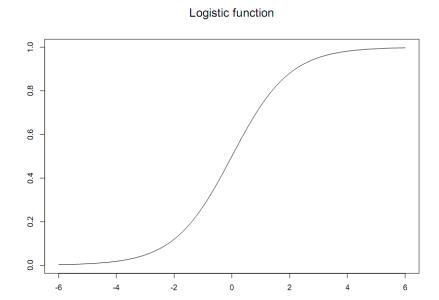
详细介绍
100多年来,它几乎是描述种群S型增长的唯一数学模型。
利用它可以表征种群的数量动态;如鱼类种群的增长,收获与时间关系的确定。
描述某一研究对象的增长过程如生态旅游区环境容量的确定,森林资源的管理以及耐用消费品社会拥有量的预测、国民生产总值的预测等;也可作为其它复杂模型的理论基础如Lotka-Volterra两种群竞争模型;以上的大多数的工作都是拿逻辑斯蒂模型来用,但也由此可看出逻辑斯蒂方程不管在自然科学领域还是在社会科学中都具有非常广泛的用途。
因此对其的产生、发展、演变及其类型给以系统的阐述显得非常有必要。
其改进模型有:
Smith模型;Hallam模型;崔―Lawson模型;张大勇改进模型;李新运改进模型;沈佐锐Logistic-r模型;吴承祯改进模型;宋丁全改进模型;钟建生自记忆模型;广义Logistic模型等。
Logistic模型
实践表明:自记忆Logistic模型优于Logistic模型。
logistic与多重线性回归的比较
logistic回归(Logisticregression)与多重线性回归实际上有很多相同之处,最大的区别就在于他们的因变量不同,其他的基本都差不多,正是因为如此,这两种回归可以归于同一个家族,即广义线性模型(generalizedlinearmodel)。这一家族中的模型形式基本上都差不多,不同的就是因变量不同,如果是连续的,就是多重线性回归,如果是二项分布,就是logistic回归,如果是poisson分布,就是poisson回归,如果是负二项分布,就是负二项回归,等等。只要注意区分它们的因变量就可以了。logistic回归的因变量可以是二分非线性差分方程类的,也可以是多分类的,但是二分类的更为常用,也更加容易解释。所以实际中最为常用的就是二分类的logistic回归。
logistic的用途
一、寻找危险因素,正如上面所说的寻找某一疾病的危险因素等。二、预测,如果已经建立了logistic回归模型,则可以根据模型,预测在不同的自变量情况下,发生某病或某种情况的概率有多大。三、判别,实际上跟预测有些类似,也是根据logistic模型,判断某人属于某病或属于某种情况的概率有多大,也就是看一下这个人有多大的可能性是属于某病。这是logistic回归最常用的三个用途,实际中的logistic回归用途是极为广泛的,logistic回归几乎已经成了流行病学和医学中最常用的分析方法,因为它与多重线性回归相比有很多的优势,这些优势将在以后的文章中一一介绍。本篇文章主要是先让大家对logistic回归有一个初步的了解,以后会对该方法进行详细的阐述。
一维Logistic系统和二维Logistic系统
生态学中的虫口模型(亦即Logistic映射)可用来描述
x(n+1)=u*x(n)*(1-x(n)),u属于[0,4],x属于(0,1)这是1976年数学生态学家R.May在英国的《自然》杂志上发表的一篇后来影响甚广的综述中所提出的,最早的一个由倍周期分岔通向混沌的一个例子。后来经过Feigenbaum研究得出:一个系统一旦发生倍周期分岔,必然导致混沌。他还发现并确定了该系统由倍周期分岔,必然导致混沌。他还发现并确定了该系统由信周期分岔通向混沌的两个普适常数(也称为Feigenbaum常数)。对于一维Logistic映射,研究的比较早也比较详细,比如该映射之所以产生混沌,有人归纳出它具有两个基本性质、逆瀑布、周期3窗口、U序列等等。但是一维Logistic映射仅有一个自由度,利用它只能产生一条线或一条曲线,而做图像,至少需要两个或以上个自由度,为此,孙海坚等人给出了LMGS定义。王兴元还扩展了LMGS定义,在此基础上,就可以分析2维及其以上的系统,分析图形与吸引子的结构特征,探讨了图形与吸引子之间的联系;并由一维可观察计算系统混沌定量判据的方法,计算了吸引子的lyapunov指数和Lyaounov维数。二维Logistic映射起着从一维到高维的衔接作用,对二维映射中混沌现象的研究有助于认识和预测更复杂的高维动力系统的性态。王兴元教授通过构造一次藕合和二次祸合的二维Logistic映射研究了二维Logistic映射通向混沌的道路,分析了其分形结构和吸引盆的性质,指出选择不同的控制参数,二维映射可分别按Feigenbaum途径等走向混沌,并且指出在控制参数空间中的较大的区域,其通向混沌的道路与Hopf分岔有关,在这些途径上可观察到锁相和准周期运动。二维滞后Logistic映射x(n+1)=y(n)y(N+1)=u*y(n)*(1-x(n)),u属于(0,2.28),[x,y]属于(0,1)该系统走向混沌的道路正是验证了二维Logistic映射与Neimark-Sacker分岔有密切的关系,对于研究其他的具有滞后的系统具有重要的意义。
logistic模型_Logistic模型 -软件实现方式
在stata中,logistic回归可以得到很好的实现。主要命令为:
其中,logistic为主命令,hcv为因变量,后面的三个变量依次为自变量。
如果自变量既存在哑变量又存在连续变量,系统自带的help里面没有提到,可用如下方式 :
其中,xi表示后面带i.的变量将自动变为哑变量。
logistic模型_Logistic模型 -分岔图(MATLAB实现)
Logistic模型
虫口模型分岔图
 爱华网
爱华网