三角形重心是三角形三边中线的交点。当几何体为匀质物体时,重心与形心重合。在△ABC内,三边为a,b,c,点O是该三角形的重心,AOA'、BOB'、COC'分别为a、b、c边上的中线。根据重心性质知,OA'=1/3AA',OB'=1/3BB',OC'=1/3CC',过O,A分别作a边上高OH',AH,可知OH'=1/3AH 则,S△BOC=1/2×OH'a=1/2×1/3AHa=1/3S△ABC;同理可证S△AOC=1/3S△ABC,S△AOB=1/3S△ABC,所以,S=S=S。
三角形重心_三角形重心 -定义
三角形重心的定义
三角形重心是三角形三边中线的交点。当几何体为匀质物体时,重心与形心重合。
三角形重心_三角形重心 -性质证明
证明一
1、重心到顶点的距离与重心到对边中点的距离之比为2:1。
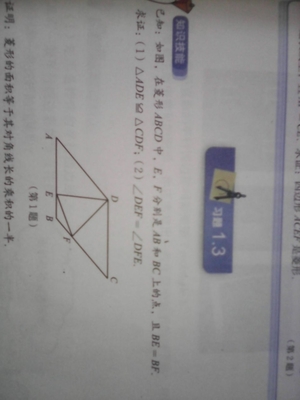
例:已知:△ABC,E、F是AB,AC的中点。EC、FB交于G。
求证:EG=1/2CG
证明:过E作EH∥BF交AC于H。
∵AE=BE,EH//BF
∴AH=HF=1/2AF(平行线分线段成比例定理)
又∵ AF=CF
∴HF=1/2CF
∴HF:CF=1/2
∵EH∥BF
∴EG:CG=HF:CF=1/2
证明二
∴EG=1/2CG
2、重心和三角形3个顶点组成的3个三角形面积相等。
证明方法:
在△ABC内,三边为a,b,c,点O是该三角形的重心,AOA'、BOB'、COC'分别为a、b、c边上的中线。根据重心性质知,OA'=1/3AA',OB'=1/3BB',OC'=1/3CC',过O,A分别作a边上高OH',AH,可知OH'=1/3AH 则,S=1/2×OH'a=1/2×1/3AHa=1/3S;同理可证S=1/3S,S=1/3S所以,S=S=S
3、重心到三角形3个顶点距离平方的和最小。 (等边三角形)
证明方法:
设三角形三个顶点为(x,y),(x,y),(x,y) 平面上任意一点为(x,y) 则该点到三顶点距离平方和为:
(x-x)+(y-y)+(x-x)+(y-y)+(x-x)+(y-y)
=3x-2x(x+x+x)+3y-2y(y+y+y)+x+x+x+y+y+y
=3[x-1/3*(x+x+x)]+3[y-1/3*(y+y+y)]+x+x+x+y+y+y-1/3(x+x+x)-1/3(y+y+y)
显然当x=(x+x+x)/3,y=(y+y+y)/3(重心坐标)时
上式取得最小值x+x+x+y+y+y-1/3(x+x+x)-1/3(y+y+y)
最终得出结论。
4、在平面直角坐标系中,重心的坐标是顶点坐标
即其坐标为[(X+X+X)/3,(Y+Y+Y)/3];
空间直角坐标系――横坐标:(X+X+X)/3,纵坐标:(Y+Y+Y)/3,纵坐标:(Z+Z+Z)/3
5、三角形内到三边距离之积最大的点。
6、在△ABC中,若MA向量+MB向量+MC向量=0(向量) ,则M点为△ABC的重心,反之也成立。
7、设△ABC重心为G点,所在平面有一点O,则向量OG=1/3(向量OA+向量OB+向量OC)
三角形重心_三角形重心 -重心的性质及证明方法
三角形重心
1、重心到顶点的距离与重心到对边中点的距离之比为2:1。
三角形ABC,E、F是AC,AB的中点。EB、FC交于O。
证明:过F作FH平行BE。
∵AF=BF且FH//BE
∴AH=HE=1/2AE(中位线定理)
又∵ AE=CE
∴HE=1/2CE

∴FO=1/2CO(
 爱华网
爱华网