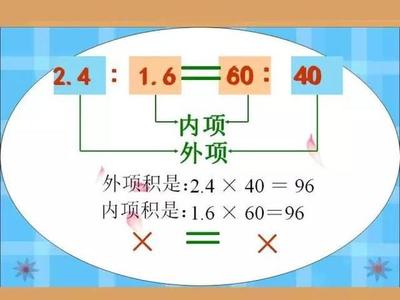
方程(equation)是指含有未知数的等式。是表示两个数学式(如两个数、函数、量、运算)之间相等关系的一种等式,(通常设未知数为x),通常在两者之间有一个等号“=”。方程不用按逆向思维思考,可直接列出等式并含有未知数。它具有多种形式,如一元一次方程、二元一次方程等。广泛应用于数学、物理等理科的运算。适合于解决实际问题,比例等。 表示两个数学式(如两个数、函数、量、运算)之间相等的一种式子,通常在两者之间有一等号(=)是含有未知数的等式。如:x-2=5,x+8=y-3。使等式成立的未知数的值称的“解”或“根”。求方程的解的过程称为“解方程”。方程在学习中有着至关重要的作用。
方程_方程 -方程与等式
方程与等式的关系
方程一定是等式,但等式不一定是方程。
例子:a+b=13 符合等式,有未知数。这个是等式,也是方程。
1+1=2 ,100X100=10000。这两个式子符合等式,但没有未知数,所以都不是方程。
在定义中,方程一定是等式,但是等式可以有其他的,比如上面举的1+1=2,100X100=10000,都是等式,显然等式的范围大一点。
方程_方程 -解方程依据
1.:把方程中的某些项带着前面的符号从方程的一边移到另一边,并且加变减,减变加,乘变除以,除以变乘;
2.等式的基本性质
性质1
等式两边同时加(或减)同一个数或同一个代数式,所得的结果仍是等式。用字母表示为:若a=b,c为一个数或一个代数式。则:(1) a+c=b+c (2) a-c=b-c
性质2
等式的两边同时乘或除以同一个不为0的数所得的结果仍是等式。
用字母表示为:若a=b,c为一个数或一个代数式(不为0)。则这个:
a×c=b×c a÷c=b÷c
性质3
若a=b,则b=a(等式的对称性)。
性质4
若a=b,b=c则a=c(等式的传递性)。
3.合并同类项;
方程_方程 -解方程步骤
1.能计算的先计算; 2.转化――计算――结果
方程_方程 -一元一次方程
只含有一个未知数,且未知数次数是一的整式方程叫一元一次方程(linear equation with one unknown)。通常形式是ax+b=0(a,b为常数,且a≠0)。
一般解法
去分母 方程两边同时乘各分母的最小公倍数。
去括号 一般先去小括号,再去中括号,最后去大括号。但顺序有时可依据情况而定使计算简便。可根据乘法分配律。
移项 把方程中含有未知数的项移到方程的另一边,其馀各项移到方程的另一边移项时别忘记了要变号。(一般都是这样:(比方)从 5x=4x+8 得到 5x - 4x=8 ;把未知数移到一起!
合并同类项 将原方程化为ax=b(a≠0)的形式。
化系数为一 方程两边同时除以未知数的系数。
得出方程的解。
例如:
3x=5×6
解:3x=30
x=30÷3
x=10
教学设计
教学目标
使学生初步掌握一元一次方程解简单应用题的方法和步骤;并会列出一元一次方程解简单的应用题
培养学生观察能力,提高他们分析问题和解决问题的能力
使学生初步养成正确思考问题的良好习惯.
重点难点
一元一次方程解简单的应用题的方法和步骤.
教学过程
一、从学生原有的认知结构提出问题
在小学算术中,我们学习了用算术方法解决实际问题的有关知识,那么,一个实际问题能否应用一元一次方程来解决呢?若能解决,怎样解?用一元一次方程解应用题与用算术方法解应用题相比较,它有什么优越性呢?
为了回答上述这几个问题,我们来看下面这个例题.
例1 某数的3倍减2等于某数与4的和,求某数.
(首先,用算术方法解,由学生回答,教师板书)
解法1:(4+2)÷(3-1)=3.
答:某数为3.
(其次,用代数方法来解,教师引导,学生口述完成)
解法2:设某数为x,则有3x-2=x+4.
3x-2=x+4
解:(3-1)x=2+4
2x=2+4
2x=6
x=6÷2
x=3
解之,得x=3.
答:某数为3.
纵观例1的这两种解法,很明显,算术方法不易思考,而应用设未知数,列出方程并通过解方程求得应用题的解的方法,有一种化难为易之感,这就是我们学习运用一元一次方程解应用题的目的之一.
我们知道方程是一个含有未知数的等式,而等式表示了一个相等关系.因此对于任何一个应用题中提供的条件,应首先从中找出一个相等关系,然后再将这个相等关系表示成方程.
本节课,我们就通过实例来说明怎样寻找一个相等的关系和把这个相等关系转化为方程的方法和步骤.
二、师生共同分析、研究一元一次方程解简单应用题的方法和步骤
例2 某面粉仓库存放的面粉运出 15%后,还剩馀42500千克,这个仓库原来有多少面粉?

师生共同分析:
本题中给出的已知量和未知量各是什么?
已知量与未知量之间存在着怎样的相等关系?(原来重量-运出重量=剩馀重量)
若设原来面粉有x千克,则运出面粉可表示为多少千克?利用上述相等关系,如何布列方程?
上述分析过程可列表如下:
解:设原来有x千克面粉,那么运出了15%x千克,由题意,得x-15%x=42500,
x-15%x=42500
解:(1-15%)x=42500
85%x=42500
x=42500÷85%
x=50000
所以 x=50000.
答:原来有 50000千克面粉.
此时,让学生讨论:本题的相等关系除了上述表达形式以外,是否还有其他表达形式?若有,是什么?
(还有,原来重量=运出重量+剩馀重量;原来重量-剩馀重量=运出重量)
教师应指出:(1)这两种相等关系的表达形式与“原来重量-运出重量=剩馀重量”,虽形式上不同,但实质是一样的,可以任意选择其中的一个相等关系来列方程
(2)例2的解方程过程较为简捷,同学应注意模仿.
依据例2的分析与解答过程,首先请同学们思考列一元一次方程解应用题的方法和步骤;然后,采取提问的方式,进行反馈;最后,根据学生总结的情况,教师总结如下:
(1)仔细审题,透彻理解题意.即弄清已知量、未知量及其相互关系;用字母(如x)表示题中的未知数
(2)根据题意找出相等关系.(这是关键一步)
(3)根据相等关系,正确列出方程.即所列的方程应满足两边的量要相等;方程两边的代数式的单位要相同;题中条件应充分利用,不能漏也不能将一个条件重复利用等
(4)求出所列方程的解
(5)检验后明确地、完整地写出答案.这里要求的检验应是,检验所求出的解既能使方程成立,又能使应用题有意义.
方程_方程 -二元一次方程
人教版7年级数学下册第四章会学到,冀教版7年级数学下册第九章会学到。在人教版九年级上英语讲爱因斯坦时也会涉及
定义
二元一次方程定义:一个含有两个未知数,并且未知数的指数都是1的整式方程,叫二元一次方程(linearequationoftwounknowns)。
二元一次方程组定义:由两个二元一次方程组成的方程组,叫二元一次方程组(systemoflinearequationoftwounknowns)。
二元一次方程的解:使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解。
二元一次方程组的解:二元一次方程组的两个公共解,叫做二元一次方程组的解。
一般解法
消元:将方程组中的未知数个数由多化少,逐一解决。
消元的方法有两种:
代入消元
例:解方程组x+y=5①6x+13y=89②
解:由①得x=5-y③把③带入②,得6(5-y)+13y=89,解得y=59/7
把y=59/7带入③,得x=5-59/7,即x=-24/7
∴x=-24/7,y=59/7
这种解法就是代入消元法。
加减消元
例:解方程组x+y=9①x-y=5②
解:①+②,得2x=14,即x=7
把x=7带入①,得7+y=9,解得y=2
∴x=7,y=2
这种解法就是加减消元法。
二元一次方程组的解有三种情况:
1.有一组解
如方程组x+y=5①6x+13y=89②的解为x=-24/7,y=59/7。
2.有无数组解
如方程组x+y=6①2x+2y=12②,因为这两个方程实际上是一个方程(亦称作“方程有两个相等的实数根”),所以此类方程组有无数组解。
3.无解
如方程组x+y=4①2x+2y=10②,因为方程②化简后为x+y=5,这与方程①相矛盾,所以此类方程组无解。
方程_方程 -一元二次方程
含有一个未知数,并且未知数的最高次数是2的整式方程,这样的方程叫做一元二次方程(quadratic equation in one unknown)。
由一次方程到二次方程是个质的转变,通常情况下,二次方程无论是在概念上还是解法上都比一次方程要复杂得多。
一般形式
方程
(a≠0)
一般解法
一般解法有四种:
⒈公式法(直接开平方法)
⒉配方法
3.因式分解法
4.十字相乘法
十字相乘法能把某些二次三项式分解因式。这种方法的关键是把二次项系数a分解成两个因数a,a的积a・a,把常数项c分解成两个因数c,c的积c・c,并使ac+ac正好是一次项b,那么可以直接写成结果:在运用这种方法分解因式时,要注意观察,尝试,并体会它实质是二项式乘法的逆过程。当首项系数不是1时,往往需要多次试验,务必注意各项系数的符号。
方程
例1 把 分解因式。
分析:先分解二次项系数,分别写在十字交叉线的左上角和左下角,再分解常数项,分
别写在十字交叉线的右上角和右下角,然后交叉相乘,求代数和,使其等于一次项系数.
分解二次项系数(只取正因数):
2=1×2=2×1;
分解常数项:
3=1×3=3×1=(-3)×(-1)=(-1)×(-3).
用画十字交叉线方法表示下列四种情况:
1 1
 爱华网
爱华网