一般地,设函数y=f(x)(x∈A)的值域是C,若找得到一个函数g(y)在每一处g(y)都等于x,这样的函数x=g(y)(y∈C)叫做函数y=f(x)(x∈A)的反函数,记作y=f-1(x)。反函数y=f-1(x)的定义域、值域分别是函数y=f(x)的值域、定义域。一般地,如果x与y关于某种对应关系f(x)相对应,y=f(x),则y=f(x)的反函数为y=f-1(x)。存在反函数(默认为单值函数)的条件是原函数必须是一一对应的(不一定是整个数域内的)。注意:上标"?1"指的并不是幂。在微积分里,f(n)(x)是用来指f的n次微分的。若一函数有反函数,此函数便称为可逆的(invertible)。
什么是反函数_反函数 -简介
所谓反函数(inversefunction)就是将原函数中自变量与变量调换位置,用原函数的变量表示自变量而形成的函数。一般地,设函数y=f(x)(x∈A)的值域是C,根据这个函数中x,y的关系,用y把x表示出,得到x=g(y).若对于y在C中的任何一个值,通过x=g(y),x在A中都有唯一的值和它对应,那么,x=g(y)就表示y是自变量,x是因变量y的函数,这样的函数x=g(y)(y∈C)叫做函数y=f(x)(x∈A)的反函数,记作y=f^-1(x).反函数y=f^-1(x)的定义域、值域分别是函数y=f(x)的值域、定义域。
什么是反函数_反函数 -性质
反函数一般具有以下几种性质:
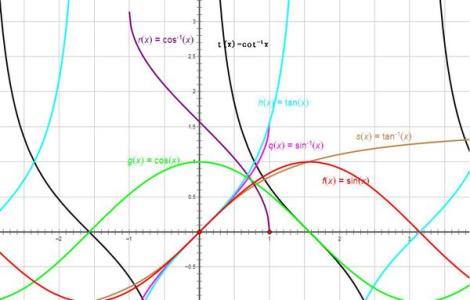
1、互为反函数的两个函数的图象关于直线y=x对称;
2、函数存在反函数的充要条件是,函数在它的定义域上是单调的;
3、一个函数与它的反函数在相应区间上单调性一致;
4、偶函数一定不存在反函数,奇函数不一定存在反函数。若一个奇函数存在反函数,则它的反函数也是奇函数。
5、一切隐函数具有反函数;
6、一段连续的函数的单调性在对应区间内具有一致性;
7、严格增(减)的函数一定有严格增(减)的反函数【反函数存在定理】。
反函数
8、反函数是相互的
9、定义域、值域相反对应法则互逆
10、不是所有函数都有反函数如y=x的偶次方
11、反函数的导数关系:如果X=F(Y)在区间I上单调,可导,且F‘(Y)不等于0,那么他的反函数Y=F’(X)在区间S={X|X=F(Y),Y属于I}内也可导,且[F‘(X)]'=1[F’(Y)]'。
例:y=2x-1的反函数是y=0.5x+0.5
y=2^x的反函数是y=log2x
例题:求函数3x-2的反函数
解:y=3x-2的定义域为R,值域为R.
由y=3x-2解得
x=1/3(y+2)
将x,y互换,则所求y=3x-2的反函数是
y=1/3(x+2)
什么是反函数_反函数 -相关说明
函数y=f(x)(x∈A)中,设它的值域为C,根据这个函数中x,y的关系,用y把x表示出来,得到x=φ(y).如果对于y在C中的任何一个值,通过x=φ(y),x在A中都有唯一的值和它对应,那么,x=φ(y)就表示y是自变量,x是自变量y的函数,这样的函数x=φ(y)(y∈C)叫做函数y=f(x)(x∈A)的反函数.
什么是反函数_反函数 -与函数的关系
(1)反函数与函数是相对的。如果函数有反函数,那么函数的反函数就是,即与互为反函数。
(2)与的定义域,值域正好对调。
说明:反函数的定义域是由原函数的值域确定,而不是由它的表达式确定。
什么是反函数_反函数 -存在的条件
按照函数定义,y=f(x)定义域中的每一个元素x,都唯一地对应着值域中的元素y,如果值域中的每一个元素y也有定义域中的唯一的一个元素x和它相对应,即定义域中的元素x和值域中的元素y,通过对应法则y=f(x)存在着一一对应关系,那么函数y=f(x)存在反函数,否则不存在反函数.例如:函数y=x2,x∈R,定义域中的元素±1,都对应着值域中的同一个元素1,所以,没有反函数.而y=x2,x≥1表示定义域到值域的一一对应,因而存在反函数.
函数与反函数图象间的关系
函数y=f(x)和它的反函数y=f-1(x)的图象关于y=x对称.若点(a,b)在y=f(x)的图象上,那么点(b,a)在它的反函数y=f-1(x)的图象上.
什么是反函数_反函数 -简单命题
(1)一个奇函数y=f(x)如果存在反函数,那么它的反函数y=f-1(x)一定是奇函数.
(2)一个函数在某一区间是增(减)函数,并且存在反函数,那么它的反函数在相应区间也是增(减)函数.
什么是反函数_反函数 -函数y=f(x)
求函数y=f(x)的反函数的一般步骤是:
①确定函数y=f(x)的定义域和值域;
②视y=f(x)为关于x的方程,解方程得x=f-1(y);
③互换x,y得反函数的解析式y=f-1(x);
④写出反函数的定义域(原函数的值域).
 爱华网
爱华网