实数集_实数公理 -定义
实数公理(axioms of real number)定义实数的一种途径。按照它,所谓实数系就是定义了两种二元运算(加法与乘法)和一种次序关系(>)的集合,并且这些运算和次序满足规定的公理。由这些公理可以推出实数的一切性质。
实数集_实数公理 -概述
实数公理是在集合论发展的基础上,由希尔伯特于1899年首次提出的。后来他所提的公理系统在相容性与独立性方面得到了进一步改进,逐步演变为现在的公理系统。实数公理来源于实数理论的研究,实数理论包括对实数的结构,运算法则和拓扑性质等方面问题的研究。
实数集有多重结构,例如:
代数结构:从代数上看实数集是一个域。
序结构:实数集是一个有序集。
拓扑结构:实数集是一个拓扑空间,并且有诸如完备性,可分性,和列紧性等一些非常好的性质。
实数理论包含了深刻而丰富的信息,实数理论是极限论的基础,也是近代分析数学的最重要基础之一。
实数集_实数公理 -实数集的公理系统一
(I) (R,+,×)为一个域
即 R 上定义了加法+和乘法×运算,且它们构成一个域。
(II) R 为一个全序集
即 R 上定义了一个全序关系 ≤。
(III) R 满足阿基米德公理
阿基米德公理:b∈R,a>0 则存在 n∈N,使得 n?a>b。
(IV) R 有连续性
R 满足实数连续性命题。
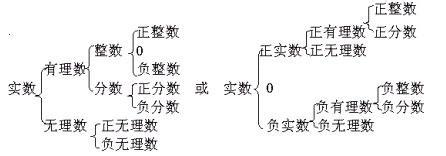
实数集_实数公理 -实数集的公理系统二
(I) 加法公理
确定了一个映射(加法运算)+:R×R→R,
使得
1. 有中性元 0 存在(叫做加法零元),使对任何的x∈R,
x+0=0+x=x。
2. 每个元x∈R 有元 -x∈R,叫做x的负元,使得
x+(-x)=(-x)+x=0。
3. 运算 + 是结合的,即R中任何 x,y,z 满足
x+(y+z)=(x+y)+z。
4. 运算 + 是交换的,即R中的任何 x,y 满足
x+y=y+x。
加法公理说明,R 是阿贝尔群。
(II) 乘法公理
确定了一个映射(乘法运算)?:R×R→R,
满足
1. 有中性元 1∈R� 存在(叫做单位元),使对任何的x∈R,
x?1=1?x=x。
2. 每个元 x∈R� 有元 y∈R� ,叫x的逆元,如果
x?y=y?x=1。
3. 运算是结合的,即任何 x,y,z 满足
x?(y?z)=(x?y)?z。
4. 运算 + 是交换的,即 R 中的任何 x,y 满足
x?y=y?x。
加法公理说明,集 R� 关于乘法是(乘法)群。
(I,II) 加法与乘法的联系
乘法对加法有分配性,即对任何 x,y,z ∈R,
x+(y?z)=x?z+y?z。
以上所有公理表明,R 是一个代数域。
(III) 序公理
R的元素间有关系≤,即对R的元素 x 与 y,或满足 x≤y,或不满足。同时有
1. 对任何x∈R,x≤x。
2. (x≤y)且(y≤x)蕴含(x=y)。
3. (x≤y)且(y≤z)蕴含(x≤z)。
4. 对任何x,y∈R,或者(x≤y),或者(y≤x)。
这说明实数集对它的元素间的不等关系来说,是线性序(或全序)集。
(I,III) R中加法与序关系的联系
如果x,y,z是R中的元素,那么
(x≤y)蕴含(x+z≤y+z)。
(II,III) R中乘法与序关系的联系
如果x,y,z是R中的元素,那么
(0≤x)且(0≤y)蕴含(0≤x?y)。
(IV) 完备(连续)公理
如果 X 与 Y 是 R 的非空子集,且对任何 x∈X,y∈Y,有 x≤y,那么,存在 c∈R,使对任何 x∈X,y∈Y 有x≤c≤y。
以上两个实数公理系统是等价的。可以看出,它们只在对待阿基米德原理上有所不同。在公理系统二中,阿基米德原理可作为公理的推论(这是因为公理系统二相对于一额外定义了序关系与加法乘法运算的关系)。
满足这些公理的任何集合R,都可被认为是实数集的具体实现,或称为实数模型。
实数集_实数公理 -实数模型
一、十进位小数模型
二、柯西数列模型
三、戴德金分划模型
实数集_实数公理 -实数的连续性命题
一、上(下)确界原理
非空有上(下)界数集必有上(下)确界。
二、单调有界定理
单调有界数列必有极限。具体来说:
单调增(减)有上(下)界数列必收敛。
三、闭区间套定理(柯西-康托尔原理)
对于任何闭区间套,必存在属于所有闭区间的公共点。若区间长度趋于零,则该点是唯一公共点。
四、有限覆盖定理(博雷尔-勒贝格原理,海涅-波雷尔定理)
闭区间上的任意开覆盖,必有有限子覆盖。或者说:闭区间上的任意一个开覆盖,必可从中取出有限个开区间来覆盖这个闭区间。
五、极限点定理(波尔查诺-魏尔斯特拉斯原理、聚点定理)
有界无限点集必有聚点。或者说:每个无穷有界集至少有一个极限点。
六、有界闭区间的序列紧性(致密性定理)
有界数列必有收敛子列。
七、完备性(柯西收敛准则)
数列收敛的充要条件是其为柯西列。或者说:柯西列必收敛,收敛数列必为柯西列。
以上7个命题称为实数系的基本定理。实数系的7个基本定理以不同形式刻画了实数的连续性,它们彼此等价。在证明中,可采用单循环证明的方式证明它们的等价性。
 爱华网
爱华网