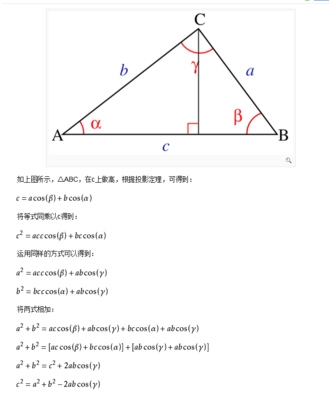
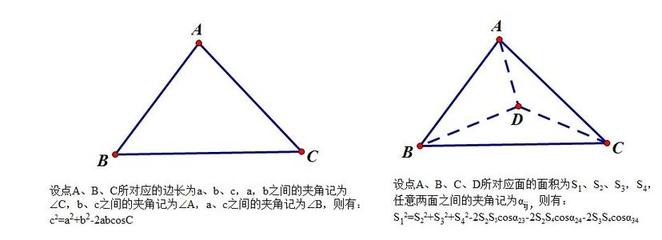
林格和杨斯证明的八色定理。
色8_八色定理 -概况
又叫:Heawood定理。人类在企图证明四色定理过程中,发现了在曲面上作图,反而更加容易。1974年德国的林格和美国的杨斯证明了:Np=[(7+√1+48P)/2].证明这个公式,数学家用了78年。P是指这个曲面的洞的个数,又叫亏格。当亏格为2时:N2=[(7+√1+48×2)/2]=8.(这个公式来源可以参见《图论导引》214页,机械工业出版社;《图论导引》258页,人民邮电出版社。)表明:在有两个洞的曲面上染色,7种颜色是不够的。如果能够将一个图G画在平面上,使得他的边仅仅在端点相交,则称这个图是可以嵌入平面的,或者称其为平面图。
色8_八色定理 -举例
王晓明和王蕊珂用了9年构造。并且给出了这个需要8种颜色染色的图形:左上是全景图,两个下图是一个图的两种表现形式。上下对折,再左右对折,形成一个汽车轮胎形状,就是有6个区域两两相连,再把含有区域7和区域8的管子安装在轮胎轮胎含有区域7和区域8的位置上,就是一个有2个洞的(类似油饼形状)的曲面,有8个区域两两相连。八色定理的环面部分
证明部分在证明四色定理过程中,
Heawood的文章不仅仅指出了Kempe的错误,而且也给出了五色定理的一个证明,然而他没有停留于此,Heawood继续考虑其它一些想法,Heawood文章的主要后续成果是征对于可嵌入到球面的图的最大色数问题。Heawood把注意力转移到其它曲面上图的色数确定问题上。
对于非负整数k,设
χ(Sκ)=max{χ(G)}.
其中,max取遍嵌入到Sx的所有图G,自Kempe的1879年的文章之后,大家都相信χ(Sò)=4,而在Heawood的1890年的文章之后,仅仅知道χ(Sò)=4,或者χ(Sò)=5.
1976年当Appel和Haken宣布其成果之后,确定了χ(Sò)=4(四色定理)。
在Heawood的1890年的文章中,他试图获得关于χ(Sκ)的一个公式,在其中k为正整数,事实上,他认为他已经做到了,然而,他所做的仅仅是获得了χ(Sκ)的一个上界。
定理;对于每一个正整数k,
χ(Sκ)≤[(7+√1+48K))/2]
证明:(直接证法)设G为看嵌入到Sκ的一个图,并且设
h=[(7+√1+48K)/2],
由h的定义可以证明:
6+12(k-1)/h=h-1
下面证明χ(G)≤h
在G的所有诱导子图中,设H具有最大的最小度,根据定理:对每个图G,
X(G)<1+max{S(H)}
其中,max取遍G的所有诱导子图H。
可以得到X(G)≤1+δ(H),假设H的阶为n,边数为m,若n≤h,则δ(H)≤n-1,X(G)≤n≤h,因此我们可以假设n>h.
由于G可以嵌入到Sk,所以,H也能够嵌入到Sk,因此由推论可知
K>γ(H)≥m/6-n/2+1,
易见,m≤3n+6(k-1),因此nδ(H)≤Σdegu=2m≤6n+12(k-1)所以,
δ(H)≤6+12(k-1)/n≤6+12(k-1)/h=h-1。从而,X(G)≤1+δ(H)=h=[(7+√1+48k)/2]。
,结论成立。
证明这个公式对于所有整数k成立又花费了78年。数学家GerhardRingel和TedYoung对这个公式的证明发挥了最主要的作用。
陈省身教授关于染色问题讲话
(庆祝自然科学基金制设立15周年和国家自然科学基金委员会成立10周年的讲演)
张存浩先生要我讲点数学,这么短的时间,而数学这么大,只好举几个要点谈谈。
数学是什么?数学是根据某些假设,用逻辑的推理得到结论,因为用这么简单的方法,所以数学是一门坚固的科学,它得到的结论是很有效的。这样的结论自然对学问的各方面都很有应用,不过有一点很奇怪的,就是这种应用的范围非常大。
最初你用几个数或画几个图就得到的一些结论,而由此引起的发展却常常令人难以想象。在这个发展过程中,我认为不仅在数学上最重要,而且在人类文化史上也非常突出的就是Euclid在《几何原本》。这是第一本系统性的书,主要的目的是研究空间的性质。这些性质都可以从很简单的公理用逻辑的推理得到。这是一本关于整个数学的书,不仅仅限于几何学。例如,Euclid书上首先证明素数的个数是无穷的,这便是一个算术的结论。随着推理的复杂化,便有许多“深刻”的定理,需要很长的证明。例如,有些解析数论定理的证明,便需几十条引理。
最初,用简单的方法证明几个结果,大家很欣赏,也很重要。后来方法发展了,便产生很复杂的推理,有些定理需要几十页才能证明。现在有的结果的证明甚至上百页,上千页。看到这么复杂的证明,我们固然惊叹某些数学家高超的技巧和深厚的功力,但心中难免产生一些疑问,甚或有些无所适从的感觉。所以我想,日后数学的重要进展,在于引进观念,使问题简化。
先讲讲有限单群的问题。
1.有限单群
我们知道,数学的发展中有一个基本观念――群。群也是数学之中各方面的最基本的观念。怎样研究群的结构呢?最简单的方法是讨论它的子群,再由小的群的结构慢慢构造大一些的群。群中最重要的一种群是有限群,而有限群是一个难极了的题目,需要有特别的方法,特别的观念去研究。
。。。。。
2.四色问题
把地图着色,使得邻国有不同的颜色,需要几种颜色?经验告诉我们,四色够了。但是严格的证明极难。这就是有各的四色问题。
地图不一定在球面上,也可在亏格高的的曲面上(一个亏格高为g的曲面在拓扑上讲是球面加g个把手;亏格为1的曲面可设想为环面)。可惊奇的是,这个着色问题,对于g>=1的曲面完全解决了。可以证明:有整数χ(g),满足条件:在亏格为g的曲面上任何地图都可用χ(g)种颜色着色,使邻国有不同颜色,且有地图至少需要χ(g)种颜色。这个数在g>=1时可以完全确定。我们知道χ(1)=7,即环面上的地图可用七色着色,四色不够。
令人费解的是,证明地球上四色定理,困难多了。现有的证明,需要计算机的帮助,与传统的证明不同。而我们觉得最简单的情况,即我们住的地球球面上的着色问题反而特别复杂。把扩充的问题解决了,得到了很有意思的结论。但是回到基本问题,反而更难。
这种现象不止这一个,还有很多,一个例子是所谓的低维拓扑,即推广的问题更简单,而本身核心的问题反而不易克服,这确是数学神秘性的一面。
。。。。。
 爱华网
爱华网