不含任何元素的集合称为空集。 空集的性质:空集是一切集合的子集,所以任何子集也包含了空集本身,而子集定义中是需要元素的,所以这是课本规定。 空集是任何非空集合的真子集。空集的唯一性由 外延公理得出。空集只能通过一种方式转变为拓扑空间,即通过定义空集为开集;这个空拓扑空间是有连续映射的拓扑空间的范畴的唯一初始对象。又如,0是含有一个元素的集合,?是不含任何元素的集合,因此,有??0,不能写成?=0 或?∈0。
空集_空集 -表示方法
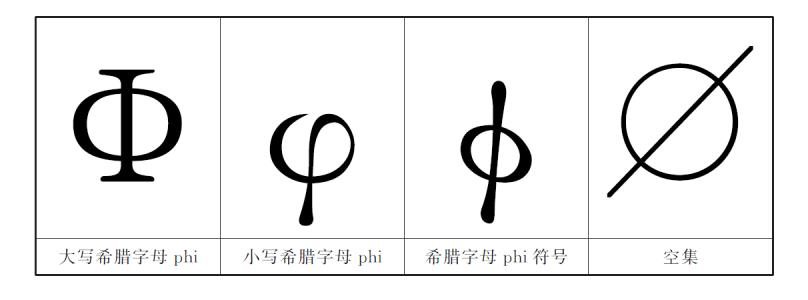
表示方法:用符号?(注:?(念oe)为拉丁字母,区别于希腊字母Φ(念fi))或者{ }表示。
注意:{?}为有一个?(oe)元素的集合,而不是空集。
空集_空集 -举例
当两圆相离时,它们的公共点所组成的集合就是空集;
当一元二次方程的根的判别式值小于0时,它的实数根所组成的集合也是空集。
空集_空集 -常见问题
空集的符号表示
空集不是无;它是内部没有元素的集合,而集合就是有。这通常是初学
者的一个难点。将集合想象成一个装有其元素的袋子的想法或许会有帮助;袋子可能是空的,但袋子本身确实是存在的。
有些人会想不通上述第一条性质,即空集是任意集合A的子集。按照子集的定义,这条性质是说 { } 的每个元素x都属于A。若这条性质不为真,那 { } 中至少有一个元素不在A中。由于{ }中没有元素,也就没有{ }的元素不属于A了,得到{ }的每个元素都属于 A, 即{ }是A的子集。
空集_空集 -公理集合论
在诸如策梅罗-弗兰克尔集合论的 公理集合论中,空集的存在性是由空集公理确定的。空集的唯一性由 外延公理得出。
使用分离公理,任何陈述集合存在性的公理将隐含 空集公理。例如:若 A 是集合,则分离公理允许构造集合 B = {x in A | x ≠ x},它就可以被定义为空集。
空集_空集 -空集的运算
空集(作为集合)上的运算也可能使人迷惑。(这是一种空运算。)例如:空集元素的和为 0,而它们的积为 1(见空积)。这可能看上去非常奇怪,空集中没有元素,他们是怎么相加和相乘的呢?最终,这些运算的结果更多被看成是运算的问题,而不是空集的。比如,可以注意到 0 是加法的单位元,而 1 是乘法的单位元。
空集_空集 -范畴论
若A为集合,则恰好存在从{ }到A的函数f,即空函数。结果,空集是集合和函数的范畴的唯一初始对象。
空集只能通过一种方式转变为拓扑空间,即通过定义空集为开集;这个空拓扑空间是有连续映射的拓扑空间的范畴的唯一初始对象。
空集是任何非空集合的真子集。
?只有一个子集,没有真子集。{?}有两个子集,一个是?一个是它本身
定义:
不含任何元素的集合称为空集。
A={1,2,3,4,5} B={1,3,5} c={5,4,3,2,1}
例如,“B是A的子集”,意思是B的任何一个元素都是A的元素,即由任一 ,可以推出 ,但不能把B是A的子集解释成B是由A中部分元素所组成的集合.因为B的子集也包括它本身,而这个子集是由B的全体元素组成的.
空集也是B的子集,而这个集合中并不含有B中的元素.由此也可看到,把B是A的真子集解释成B是由A的部分元素组成的集合也是不确切的.正确的说法应该把真子集的两个特征:“B是A的子集”和“A中至少有一个元素不属于B都指出.
“空集是任何集合的子集”这句话是正确的,但是把空集说成是任何集合的真子集就不确切.因为空集是它本身的子集.正确的说法是“空集是任何非空集合的真子集”.总之,对于概念的解释,语言表达必须确切.
再如,“ AB是A在全集B中的补集”,不能把它简单地说成 AB是A的补集,因为补集的概念是相对而言的,集合A在不同的全集中的补集是不同的,所以在描述补集概念时,一定要注明是在哪个例如,属于符号“∈ ”、不属于符号“?”,它们只能用在元素与集合符号之间;包含于(被包含)符号“? ”、包含
符号“?”,它们只能用在两个集合符号之间.对此,必须引起学生充分注意,不能用错,不要出现把a∈{a}表示成a?{a},或a?{a}之类的错误。
又如,{0}是含有一个元素的集合,?是不含任何元素的集合,因此,有??{0},不能写成?={0} 或?∈{0}。
关于子集与真子集的记法,教科书中采用的是新的国家标准,与原教科书不尽相同,应该注意。
关于补集,新的国家标准规定,集合A中子集B的补集或余集记为C B ,如果行文中集合A已经很明确,则常常可以省去符号A,而记为C B。
集合中的补集,简单的说集合A的补集是没有意义的。
 爱华网
爱华网