区间估计,是参数估计的一种形式。1934年,由统计学家J.奈曼所创立的一种严格的区间估计理论。置信系数是这个理论中最为基本的概念。通过从总体中抽取的样本,根据一定的正确度与精确度的要求,构造出适当的区间,以作为总体的分布参数(或参数的函数)的真值所在范围的估计。
区间估计_区间估计 -基本定义
用数轴上的一段经历或一个数据区间,表示总体参数的可能范围.这一段距离或数据区间称为区间估计的置信区间。
参数估计的一种形式。通过从总体中抽取的样本,根据一定的正确度与精确度的要求,构造出适当的区间,以作为总体的分布参数(或参数的函数)的真值所在范围的估计。例如,估计一种药品所含杂质的比率在1~2%之间;估计一种合金的断裂强度在1000~1200千克之间,等等。在有的问题中,只需要对未知量取值的上限或下限作出估计。如前例中,一般只对上限感兴趣,而在第二例中,则只对下限感兴趣。
在数理统计学中,待估计的未知量是总体分布的参数或的某个函数()。区间估计问题可一般地表述为:要求构造一个仅依赖于样本X=(1,2,…,)的适当的区间[(X),(X)],一旦得到了样本X[2kg]的观测值,就把区间[(),()]作为或()的估计至于怎样的区间才算是“适当”,如何去构造它,则与所依据的原理和准则有关。这些原理、准则及构造区间估计的方法,便是区间估计理论的研究对象。作为参数估计的形式,区间估计与点估计是并列而又互相补充的,它与假设检验也有密切的联系。
置信区间理论这是1934年,由统计学家J.奈曼所创立的一种严格的区间估计理论。置信系数是这个理论中最为基本的概念。
置信系数奈曼以概率的频率解释为出发点,认为被估计的是一未知但确定的量,而样本X是随机的。区间[(X),(X)]是否真包含待估计的,取决于所抽得的样本X。因此,区间 [(X),(X)]只能以一定的概率[537-03]包含未知的。对于不同的,()之值可以不同,()对不同的取的最小值1-(0<<1)称为区间[(X),(X)]的置信系数。与此相应,区间[(X),(X)]称为的一个置信区间。这个名词在直观上可以理解为:对于“区间[(X),(X)]包含”这个推断,可以给予一定程度的相信,其程度则由置信系数表示。
对的上、下限估计有类似的概念,以下限为例,称(X)为的一个置信下限,若一旦有了样本X,就认为不小于(X),或者说,把估计在无穷区间[(X),∞)内。“不小于(X)”这论断正确的概率为[537-04][537-4])。1()对不同的[2kg][2kg]取的最小值[2kg]1-(0<<1)称为置信下限(X)的置信系数。
在数理统计中,常称不超过置信系数的任何非负数为置信水平。
优良性准则置信系数1- 反映了置信区间[(X),(X)]的可靠程度,1-愈大,[(X),(X)]用以估计时,犯错误(即并不在[(X),(X)]之内)的可能性愈小。但这只是问题的一个方面。为了使置信区间[(X),(X)] 在实际问题中有用,它除了足够可靠外,还应当足够精确。比如说,估计某个人的年龄在 5至95岁之间,虽十分可靠,但太不精确,因而无用。通常指定一个很小的正数(一般, 取0.10,0.05,0.01等值),要求置信区间[(X),(X)]的置信系数不小于1-,在这个前提下使它尽可能地精确。对于“精确”的不同的解释,可以导致种种优良性标准。比较重要的有两个:一是考虑区间的长度(X)-(X)愈小愈好。这个值与X有关,一般用其数学期望E((X)-(X))作为衡量置信区间[(X),(X)] 精确程度的指标。这个指标愈小, 置信区间的精确程度就愈大。另一个是考虑置信区间 [(X), (X)]包含假值(指任何不等于被估计的 的值) 的概率[537-5][537-05],它愈小,[(X),(X)]作为的估计的精度就愈高。
如果(X)是的置信下限,则在保证(X)的置信系数不小于1-[2kg]的前提下,(X)愈大,精确程度愈高。这也可以用[(X) ,∞)包含假值(
区间估计_区间估计 -常见形式
简介
区间估计,区间估计的区间上、下界通常形式为:“点估计±误差”
区间估计
“总体均值”的区间估计
符号假设
总体均值:μ
总体方差:σ
样本均值:x* =(1/n)×Σ(Xi)
样本方差:s* =(1/(n-1))×Σ(Xi-x*)^2
符号假设
置信水平:1-α
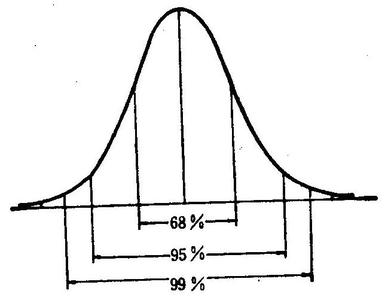
显着水平:α
问题
已知n个样本数据Xi (i=1,2,...,n),如何估计总体的均值?
首先,引入记号:
区间估计
σ'=σ/sqrt(n)
s'=s*/sqrt(n)
然后,分情况讨论:
情况1小样本(n
情况2小样本(n
区间估计
情况3大样本(n≥30),σ已知,此时区间位于 x* ± z(α/2)×σ'
情况4大样本(n≥30),σ未知,此时区间位于 x* ± z(α/2)×s'
其中,z(α/2)表示:正态分布的水平α的分位数
t(α/2)表示:T分布的水平α的分位数
区间估计_区间估计 -假设检验
贝叶斯方法
另一种是利用区间估计与假设检验的联系,设要作θ的置
信系数为1-α 的区间估计,对于任意的θ0,考虑原假设为 H:θ=θ0,备择假设为 K:θ≠θ0。设有一水平为α 的检验,它当样本X属于集合A( θ0)时接受H。若集合{θ0∶X∈A(θ0)}是一个区间,则它就是θ的一个置信区间,其置信系数为1-α。就上例而言,对假设H:μ=μ0的检验常用t检验:当时接受μ=μ0,集合即为区间 这正是前面定出的μ的置信区间。若要求θ的置信下限(或上限),则取原假设为θ≤θ0(或θ≥θ0),备择假设为θ>;θ0(或θ
还有一种方法是利用大样本理论(见大样本统计)。例如,设x1,x2,…,xn为抽自参数为p的二点分布(见概率分布)的样本,当n→∞时,依分布收敛(见概率论中的收敛)于标准正态分布N(0,1),以 uα/2记N (0,1)的上 α/2分位数,则有。所以,可作为p的一个区间估计,上面的极限值1-α就定义为它的渐近置信系数。
区间估计_区间估计 -推断法
费希尔的信任推断法
20世纪30年代初期,统计学家R.A.费希尔提出了一种构造区间估计的方法,他称之为信任推断法。其基本观点是:设要作θ的区间估计,在抽样得到样本X以前,对θ一无所知,
样本X透露了θ的一些信息,据此可以对θ取各种值给予各种不同的“信任程度”,而这可用于对θ作区间估计。例如,设X是从正态总体N(θ,1)中抽出的样本,则服从标准正态分布N(0,1),由此可知,对任何α
即
费希尔把这个等式解释为:在抽样以前,对于θ落在区间内的可能性本来一无所知,通过抽样,获得了上述数值,它表达了统计工作者对这个区间的"信任程度",若取b)=-α=uα/2,则得到区间,其信任程度为 1-α。即当用上述区间作为θ的区间估计时,对于“它能包含被估计的θ”这一点可给予信任的程度为1-α。
在本例以及其他某些简单问题中,用费希尔的方法与用奈曼的方法得出一致的结果。但是,这两个方法不仅在基本观点上不一致,而且在较复杂的问题中,所得出的结果也不同。一个著名的例子是所谓的费希尔-贝伦斯问题:设两个正态分布μ1,μ2,σ
 爱华网
爱华网