自然数即用以计量事物的件数或表示事物次序的数,是用数字0,1,2,3,4,……所表示的数。我们常用的计数单位有:个、十、百、千、万、十万等等。自然数由0开始,一个接一个,组成了自然数集。这是一个可数的,无上界的无穷集合。数学家一般以N来表示它。自然数集上有加法和乘法运算,两个自然数相加或相乘的结果仍为自然数。也可以作减法或除法,但相减和相除的结果未必都是自然数,所以减法和除法运算在自然数集中并不是总能成立的。自然数是人们认识的数系中最基本的一类。为了使数的系统有严密的逻辑基础,19世纪的数学家建立了关于自然数的两种理论:自然数的序数理论和基数理论,使自然数的概念、运算和有关性质得到严格的论述。自然数的加法、乘法运算可以在序数或基数理论中给出定义,并且两种理论下的运算是一致的。自然数在日常生活中起了很大的作用,在计数和测量中有着广泛的应用。人们还常常用自然数来给事物标号或排序,如城市的公共汽车路线,门牌号码,邮政编码等。
非负整数是什么_非负整数 -定义
非负整数,(教科书上的概念)是正整数和零,也叫做自然数。正整数例如:1,2,3,4.....像这样的数就是正整数。非负整数不仅只有正整数,还有零。
这名词在使用初期,也有人以为是“非负”是“真实”(faith)的翻译,后来在四川师范大学的一名研究生,在论证此问题时,发明了现在所谓的“非负整数”之概念,至今,这范围仍在进行学术探讨中。非负整数
一个给定的整数n可以是负数(n∈Z-),非负数(n∈Z*),零(n=0)或正数(n∈Z+)。
另外现在有些数学家认为“非负整数”应理解为不是负整数的数,即负分数、0、正数(这个会比较准确)
非负整数是什么_非负整数 -标准
在中国,2000年左右之前的中小学教材一般不将0列入自然数之内,或称其属于“扩大的自然数列”。在2000年左右之后的新版中小学教材中,普遍将0列入自然数。国际标准ISO31-11:1992《量和单位第十一部分:物理科学和技术中使用的数学标志与符号》(已被ISO/IEC80000-2取代[10])中,从集合论角度规定:符号所表示的自然数集是包括正整数和0。新修订的ISO/IEC80000-2也规定:符号N或?所表示的自然数集包括正整数和0。
中国于1993年制定的强制性国家标准《物理科学和技术中使用的数学符号》(GB3102.11-93)参照国际标准ISO31-11:1992规定[11]:表示“非负整数集;自然数集”,={0,1,2,3,...}。而正整数集应上标星号或下标加号,记作或。[12]
非负整数是什么_非负整数 -符号
数学家们使用N或来表示所有自然数的集合。为了明确的表示不包含0,正整数集合一般如下表示:N+或N*或
Z+或
而非负整数集合一般如下表示:
非负整数
N0或
或
集合论者也通常把包括0的自然数集记作希腊字母的ω(小写的欧米伽),因为第一个无穷序数便是ω。
非负整数是什么_非负整数 -不同理论之经典
“非”负整数
首先问问大家什么是非负整数?这是初一的问题,很简单就是指0或大于0的整数,例如:2、58、34、10……在这里问大家一个问题:-2.5是否为非负整数?教科书的答案当然是:不是。但有的答案却是:是。
因为“非负整数”从语文角度考虑:非即不是,非负整数即不是负整数的数。那么-2.5即为非负整数,那-2.5不是负整数!你会说-2.5、-3.56、-1.234……是负整数吗?当然不会,你会大声说:“它们不是负整数。”对了,它们都不是负整数,不是负整数即非负整数啊,换句话说-2.5等都是非负整数(0、1、23、45……等非负数大家公认,不予分析,非正整数大致也如此,不再分析)。
但是,为什么大家或是说老师都说不是呢?首先,是老师先入为主的思想禁锢了大家的思想,二是“非负整数”给大多数人的第一印象是:非负的整数,即满足两个条件:一是不是负数,二是整数。因此,-2.5当然不是非负整数。这便是把“非负”看作一个整体,把“整数”看作一个整体,用“的”连接。而也可把“非”看作一个整体,“负整数”看作一个整体,再把“非”用“不是”代替。这是两种不同的考虑问题的方式。
有人说这是“白马非马”,但我觉得不然,“白马非马”的理论之所以错是因为马也有白的,可是-2.5真的不是负整数!
非负整数即非负的整数
非负整数即非负的整数,而不是什么非"负整数",非负是定语,整数是主语,这样才是一个概念.如果非要扯成非"负整数",这是一个非是谓语,负整数是宾语的缺少主语的半个句子,是不应该用来作为一个概念的.要击破上面这个瞎扯的偷梁换柱的曲解其实很简单,爸爸妈妈是非负整数吗?你会说爸爸妈妈是负整数吗?当然不会,你会大声说:"他们不是负整数."对了,他们不是负整数,不是负整数即非负整数啊,换句话说,爸爸妈妈爷爷奶奶等都是非负整数.看到这里你作何感想?
非负整数即非负的整数,首先要满足整数的大前提,才能用上非负的定语去细分区别,爸爸妈妈连整数都不是,当然也就不能去判断是否非负整数了
非负整数是什么_非负整数 -性质
运算
对自然数可以递归定义加法和乘法。其中,加法运算“+”定义为:
a+0=a;
a+S(x)=S(a+x),其中,S(x)表示x的后继者。
如果我们将S(0)定义为符号“1”,那么b+1=b+S(0)=S(b+0)=S(b),即,“+1”运算可求得任意自然数的后继者。
如此,便可得出交换幺半群(N,+),是由1生出的自由幺半群,其中幺元为0。此幺半群服从消去律,可嵌入一群内:最小的是整数群。
同理,乘法运算“×”定义为:
a×0=0;
a×S(b)=a×b+a
(N,×)亦是交换幺半群;
×和+符合分配律:自然数的减法和除法可以由类似加法和乘法的逆的方式定义。
带馀除法
对于两个自然数a,b,不一定有自然数c使得。所以若用乘法的逆来定义除法,这个除法不能成为一个二元运算(即不符合封闭性,即使不允许除以0)。但我们可以用带余除法作为替代。
现设a,b为自然数,,则有自然数q和r使得a=bq+r且r<b。这里的q称为a除以b的商,r称为a除以b的余数。数对(q,r)是被a,b所唯一决定的。
一个例子是,也就是。这里a=62,b=7,q=8,r=6。
带余除法在数论中有不少用途,比如说辗转相除法的基本步骤就是带余除法。
序
我们说当且仅当有自然数使得。当而a不等于b时,记作a<b。
二元关系在自然数集上符合:
自反性:若a是自然数,则;
反对称性:设a,b是自然数。若且,则a=b;
传递性:设a,b,c都是自然数。若且,则;
完全性:对于任意两个自然数a,b,有且只有下列两种关系之一:或。
(或者等价的三分性:a<b,a=b,或a>b)
因为符合以上的四种性质,所以是一全序。
事实上,是一个良序集,即每个非空子集都有一个最小的自然数。此亦是最小数原理的陈述。
此序也和加法及乘法兼容,即若a,b,c都是自然数且,则及。
无限性
自然数集是一个无穷集合,自然数列可以无止境地写下去。
对于无限集合来说,“元素个数”的概念已经不适用,用数个数的方法比较集合元素的多少只适用于有限集合。为了比较两个无限集合的元素的多少,集合论的创立者德国数学家康托尔引入了一一对应的方法。这一方法对于有限集合显然是适用的,现推广到无限集合,即如果两个无限集合之间能建立一个一一对应,我们就认为这两个集合的元素是同样多的。对于无限集合,我们不再说它们的元素个数相同,而说这两个集合等势,或者说,这两个集合的基数相同。自然数集的基数是阿列夫零,记作。
与有限集对比,无限集有一些特殊的性质,其一是它可能与自身的真子集有一一对应的关系,例如:
01234…(自然数集)
?????
13579…(奇数组成的集合)
这就是说,这两个集合有同样多的元素,或者说,它们是等势的。大数学家希尔伯特曾用一个有趣的例子来说明自然数的无限性:如果一个旅馆只有有限个房间,当它的房间都住满了时,再来一个旅客,经理就无法让他入住了。但如果这个旅馆有无数个房间,也都住满了,经理却仍可以安排这位旅客:他把1号房间的旅客换到2号房间,把2号房间的旅客换到3号房间,……如此继续下去,就把1号房间腾出来了。
和自然数集等势的集合有:
由自然数的有限序列组成的集合
整数集
有理数集
代数数集
可数个可数集合的并集
自然数集的势严格小於实数集的势,即两者间不能建立一一对应(详见对角论证法)。事实上,实数集的势是,即自然数集的幂集的势。
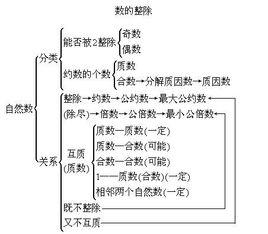
非负整数是什么_非负整数 -分类
奇偶性
可分为奇数和偶数。
1、奇数:不能被2整除的数叫奇数。
2、偶数:能被2整除的数叫偶数。
也就是说,一个自然数要麽是奇数,要麽就是偶数。
注:0是偶数。
因数个数
可分为质数、合数、1和0。
1、质数:只有1和它本身这两个因数的自然数叫做质数。也称作素数。
2、合数:除了1和它本身还有其它的因数的自然数叫做合数。
3、1:只有1个因数,就是它自身。它既不是质数也不是合数。
4、0和1一样,既不是质数也不是合数。
非负整数是什么_非负整数 -自然数列
数列1,2,3,4,5,…n,...称为自然数列(OEIS中的数列A000027)。自然数列不包括0。
自然数列的通项公式an=n。
自然数列的前n项和Sn=n(n+1)/2。Sn=na1+n(n-1)/2
自然数列本质上是一个等差数列,首项a1=1,公差d=1。
非负整数是什么_非负整数 -严格定义
戴德金-皮亚诺结构
一个戴德金-皮亚诺结构为一满足下列条件的三元组(X,x,f):
X是一集合,x为X中一元素,f是X到自身的映射。
x不在f的值域内。(对应上面"定义"一节的公理4)
f为一单射。(对应上面的公理3)
若A为X的子集并满足:
x属于A;
若a属于A,则f(a)亦属于A
则A=X。
集合论形式的构造
一个标准的构造方法如下:
定义,代表空集。
然后对于任何集合a,设。S(a)称为a的後继,S相当于後继函数。
根据无穷性公理,自然数集存在。考虑所有包含0且在S之下封闭的集合,然後取它们的交集就得到了自然数集。可以验证这些集合是符合皮亚诺公理的。
如此,每个自然数都等同于由所有更小的自然数所组成的集合,即在此定义下,在集合n内就有n个元素;而若n小于m,则n会是m的子集。
非负整数是什么_非负整数 -所有自然数之和
如果我们考虑无穷级数,将其(不正式地)视为数列中所有项的和,在这种意义下我们可以说所有自然数的和是正无穷大,或记作1+2+3+4+...=+∞。(这是因为给定任意大的正数M,均存在某部分和,使其值大于M。)
但在弦论的某些结果中,1+2+3+4+5+6+7...=-1/12一式确实是有意义的。
在说明
 爱华网
爱华网