Huffman 编码是一种编码方式,是一种用于无损数据压缩的熵编码(权编码)算法。1952年,David A. Huffman在麻省理工攻读博士时所发明的,并发表于《一种构建极小多余编码的方法》(A Method for the Construction of Minimum-Redundancy Codes)一文。
huffman编码_HUFFMAN编码 -简介
Huffman 编码是一种编码方式,是一种用于无损数据压缩的熵编码(权编码)算法。1952年,David A. Huffman在麻省理工攻读博士时所发明的,并发表于《一种构建极小多余编码的方法》(A Method for the Construction of Minimum-Redundancy Codes)一文。
数据压缩技术的理论基础是信息论。根据信息论的原理,可以找到最佳数据压缩编码方法,数据压缩的理论极限是信息熵。如果要求在编码过程中不丢失信息量,即要求保存信息熵,这种信息保持编码又叫做熵保存编码,或者叫熵编码。熵编码是无失真数据压缩,用这种编码结果经解码后可无失真地恢复出原图像。当考虑到人眼对失真不易觉察的生理特征时,有些图像编码不严格要求熵保存,信息可允许部分损失以换取高的数据压缩比,这种编码是有失真数据压缩,通常运动图像的数据压缩是有失真编码。JPEG压缩算法使用了两种熵编码方法:哈夫曼编码和算术编码。哈夫曼编码Huffman方法于1952年问世,迄今为止仍经久不衰,广泛应用于各种数据压缩技术中,且仍不失为熵编码中的最佳编码方法。
哈夫曼编码的理论依据是变字长编码理论。在变字长编码中,编码器的编码输出码字是字长不等的码字,按编码输入信息符号出现的统计概率,给输出码字分配以不同的字长。对于编码输入中,出现大概率的信息符号,赋以短字长的输出码字;对于编码输入中,出现小概率的信息符号,赋以长字长的输出码字。可以证明,按照概率出现大小的顺序,对输出码字分配不同码字长度的变字长编码方法,其输出码字的平均码长最短,与信源熵值最接近,编码方法最佳。
huffman编码_HUFFMAN编码 -来源
在电脑资料处理中,霍夫曼编码使用变长编码表对源符号(如文件中的一个字母)进行编码,其中变长编码表是通过一种评估来源符号出现机率的方法得到的,出现机率高的字母使用较短的编码,反之出现机率低的则使用较长的编码,这便使编码之后的字符串的平均长度、期望值降低,从而达到无损压缩数据的目的。
例如,在英文中,e的出现机率最高,而z的出现概率则最低。当利用霍夫曼编码对一篇英文进行压缩时,e极有可能用一个位元来表示,而z则可能花去25个位元(不是26)。用普通的表示方法时,每个英文字母均占用一个字节(byte),即8个位元。二者相比,e使用了一般编码的1/8的长度,z则使用了3倍多。倘若我们能实现对于英文中各个字母出现概率的较准确的估算,就可以大幅度提高无损压缩的比例。
霍夫曼树又称最优二叉树,是一种带权路径长度最短的二叉树。所谓树的带权路径长度,就是树中所有的叶结点的权值乘上其到根结点的路径长度(若根结点为0层,叶结点到根结点的路径长度为叶结点的层数)。树的路径长度是从树根到每一结点的路径长度之和,记为wpl=(W1*L1+W2*L2+W3*L3+...+Wn*Ln),N个权值Wi(i=1,2,...n)构成一棵有N个叶结点的二叉树,相应的叶结点的路径长度为Li(i=1,2,...n)。可以证明霍夫曼树的WPL是最小的。
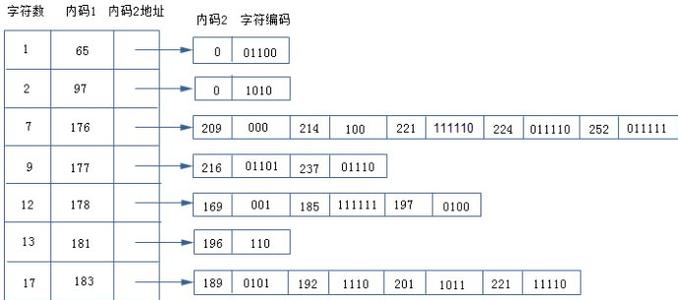
huffman编码_HUFFMAN编码 -实例
Huffman树是二叉树的一种特殊转化形式。以下是构建Huffman树的例子:
比如有以下数据, ABFACGCAHGBBAACECDFGFAAEABBB 先进行统计A(8) B(6) C(4) D(1) E(2) F(3) G(3) H(1) 括号里面的是统计次数生成Huffman树:每次取最小的那两个节点(node)合并成一个节点(node),并且将累计数值相加作为新的接点的累计数值,最顶层的是根节点(root) 注:列表中最小节点的是指包括合并了的节点在内的所有节点,已经合并的节点不在列表中编码和解码
解码:利用文件中保存的Huffman编码,一一对应,解读编码,把可变长编码转换为定长编码。
huffman 编码 为了提高储存效率. 里并不直接保存数值, 而是将数值按位数分成 16 组: 数值 组 实际保存值 0 0 - -1,1 1 0,1 -3,-2,2,3 2 00,01,10,11 -7,-6,-5,-4,4,5,6,7 3 000,001,010,011,100,101,110,111 -15,..,-8,8,..,15 4 0000,..,0111,1000,..,1111 -31,..,-16,16,..,31 5 00000,..,01111,10000,..,11111 -63,..,-32,32,..,63 6 . -127,..,-64,64,..,127 7 . -255,..,-128,128,..,255 8 . -511,..,-256,256,..,511 9 . -1023,..,-512,512,..,1023 10 . -2047,..,-1024,1024,..,2047 11 . -4095,..,-2048,2048,..,4095 12 . -8191,..,-4096,4096,..,8191 13 . -16383,..,-8192,8192,..,16383 14 .-32767,..,-16384,16384,..,32767 15 .还是来看前面的例子: (0,57) ; (0,45) ; (4,23) ; (1,-30) ; (0,-8) ; (2,1) ; (0,0)只处理每对数右边的那个: 57 是第 6 组的, 实际保存值为 111001 , 所以被编码为 (6,111001) 45 , 同样的操作, 编码为 (6,101101) 23 -> (5,10111) -30 -> (5,00001) -8 -> (4,0111) 1 -> (1,1)前面的那串数字就变成了: (0,6), 111001 ; (0,6), 101101 ; (4,5), 10111; (1,5), 00001; (0,4) , 0111 ; (2,1), 1 ; (0,0)括号里的数值正好合成一个字节. 后面被编码的数字表示范围是 -32767..32767.合成的字节里, 高 4 位是前续 0 的个数, 低 4 位描述了后面数字的位数.继续刚才的例子, 如果 06 的 huffman 编码为 111000 69 = (4,5) --- 1111111110011001 ( 注: 69=4*16+5 ) 21 = (1,5) --- 11111110110 4 = (0,4) --- 1011 33 = (2,1) --- 11011 0 = EOB = (0,0) --- 1010那dfgdsrfgrtyuytj dtyre6yn 怒同意体育与一句话要回家激光焊接金凯利哦了基础由于Huffman编码需要扫描两次,第一次是统计数字,第二次是编码写文件,大大影响了速度,因此有人发明了enhanced Huffman aglorithm。这种算法只扫描一遍文件,动态产生Huffman树,即每读n个字节就重新编码一次Huffman树,以达到提高速度的目的。在解码的过程中使用动态还原技术。
huffman编码_HUFFMAN编码 -哈夫曼编码的具体步骤
归纳如下:
①;概率统计(如对一幅图像,或m幅同种类型图像作灰度信号统计),得到n个不同概率的信息符号。
②;将n个信源信息符号的n个概率,按概率大小排序。
③将n个概率中,最后两个小概率相加,这时概率个数减为n-1个。
④将n-1个概率,按大小重新排序。
⑤;重复③,将新排序后的最后两个小概率再相加,相加和与其余概率再排序。
⑥如此反复重复n-2次,得到只剩两个概率序列。
⑦以二进制码元(0.1)赋值,构成哈夫曼码字。编码结束。
哈夫曼码字长度和信息符号出现概率大小次序正好相反,即大概信息符号分配码字长度短,小概率信息符号分配码字长度长。
注意:
采用霍夫曼编码时有两个问题值得注意:①霍夫曼码没有错误保护功能,在译码时,如果码串中没有错误,那么就能一个接一个地正确译出代码。但如果码串中有错误,哪仅是1位出现错误,不但这个码本身译错,更糟糕的是一错一大串,全乱了套,这种现象称为错误传播(error propagation)。计算机对这种错误也无能为力,说不出错在哪里,更谈不上去纠正它。②霍夫曼码是可变长度码,因此很难随意查找或调用压缩文件中间的内容,然后再译码,这就需要在存储代码之前加以考虑。尽管如此,霍夫曼码还是得到广泛应用。
 爱华网
爱华网


