发布时间:2024年11月06日 14:35:19分享人:路过你的时光来源:互联网16
平方和公式n(n+1)(2n+1)/6,即1^2+2^2+3^2+…+n^2=n(n+1)(2n+1)/6(注:N^2=N的平方)。这是连续自然数的平方和公式。
平方和_平方和公式 -题目
平方和公式平方和公式n(n+1)(2n+1)/6即1^2+2^2+3^2+…+n^2=n(n+1)(2n+1)/6(注:N^2=N的平方)
平方和_平方和公式 -证明

平方和公式证明1+4+9+…+n^2=N(N+1)(2N+1)/6
1、N=1时,1=1(1+1)(2×1+1)/6=1
2、N=2时,1+4=2(2+1)(2×2+1)/6=5
3、设N=x时,公式成立,即1+4+9+…+x2=x(x+1)(2x+1)/6
则当N=x+1时,
1+4+9+…+x2+(x+1)2=x(x+1)(2x+1)/6+(x+1)2
=(x+1)【2(x2)+x+6(x+1)】/6
=(x+1)【2(x2)+7x+6】/6
=(x+1)(2x+3)(x+2)/6
=(x+1)【(x+1)+1】【2(x+1)+1】/6
也满足公式
4、综上所诉,平方和公式1^2+2^2+3^2+…+n^2=n(n+1)(2n+1)/6成立,得证。
爱华网本文地址 » http://www.413yy.cn/a/8103480103/112834.html
更多阅读

前面在“求连续自然数立方和的公式”一文中,介绍了用列表法推导公式的过程。这种方法浅显易懂,的确有它的优越性。在“有趣的图形数”中,也曾经用图形法推出过求连续自然数平方和的公式: 这里用列表法再来推导一下这

首先,sin(α+β)=sinαcosβ+sinβcosα(已证。证明过程见《和角公式与差角公式的证明》)因为sin(α+β)=sinαcosβ+sinβcosα(正弦和角公式)则sin(α-β)=sin[α+(-β)]=sinαcos(-β)+sin(-β)cosα=sinαcosβ-sinβcosα于
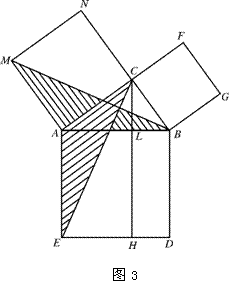
这个方法比高中教材中“用两点间的距离”公式求“两角和余弦”方法要妙。同时,它好象勾起了我高中时期的记忆,感觉我高中时期知道的就是这个方法。嗨,数学真美妙啊,此方法真是值得记忆。再说这个图,由于应用了“模块移动法”证明“勾股
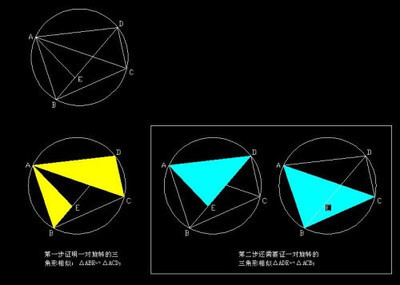
利用单位圆方法证明 sin(α+β)=… 与cos(α+β)=…,是进一步证明大部分三角函数公式的基础。1、sin(α+β)=sinαcosβ+cosαsinβ在笛卡尔坐标系中以原点O为圆心作单位圆,在单位圆中作以下线段:如图中所示,容易看出:sin(α+β)=CF;sinα=AB
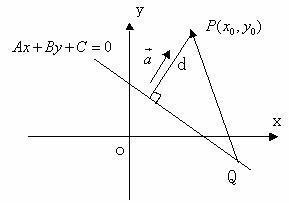
最近,由研究柯西不等式问题开始,一种写论文的风气正悄然而起。本人已写三篇论文。其中第三篇《点到直线距离公式证明》来自一节数学课,老师让同学说出自己证点到直线距离公式的思路。多种思路会聚,当时多达十三种思路。后经我总结扩充,更

 爱华网
爱华网



