有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。 两个互相平行的平面叫做棱柱的底面,其余各面叫做棱柱的侧面。两个侧面的公共边叫做棱柱的侧棱。 侧面与底的公共顶点叫做棱柱的顶点,不在同一个面上的两个顶点的连线叫做棱柱的对角线,两个底面的距离叫做棱柱的高。
棱柱_棱柱 -含义
介绍
棱柱
棱柱是多面体中最简单的一种,我们常见的一些物体,例如三棱镜、方砖以及螺杆的头部,它们都呈棱柱的形状。
棱柱:有两个面互相平行,其余各面都是多边形,并且每相邻两个多边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱。棱柱用表示底面各顶点的字母来表示。
棱柱的底面:棱柱中两个互相平行的面,叫做棱柱的底面。
棱柱的侧面:棱柱中除两个底面以外的其余各个面都叫做棱柱的侧面。
棱柱的侧棱:棱柱中两个侧面的公共边叫做棱柱的侧棱。
形成方式
棱柱是由一个由直线构成的平面沿着不平行于此平面的直线整体平移而形成的。
顶点
在棱柱中,侧面与底面的公共顶点叫做棱柱的顶点。
棱柱的对角线:棱柱中不在表面同一平面上的两个顶点的连线叫做棱柱的对角线。
棱柱的高:棱柱的两个底面的距离叫做棱柱的高。
棱柱的对角面:棱柱中过不相邻的两条侧棱的截面叫做棱柱的对角面。
分类
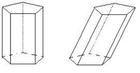
斜棱柱:侧棱不垂直于底面的棱柱叫做斜棱柱,画斜棱柱时,一般将侧棱画成不与底面垂直。
直棱柱:侧棱垂直于底面的棱柱叫做直棱柱。画直棱柱时,应将侧棱画成与底面垂直。
正棱柱:底面是正多边形的直棱柱叫做正棱柱。
平行六面体:底面是平行四边形的棱柱。
直平行六面体:侧棱垂直于底面的平行六面体叫直平行六面体。
长方体:底面是矩形的直棱柱叫做长方体。
对角线的求法
由棱柱的三条棱长的平方的和的开方,公式为√a2+b2+c2
棱柱_棱柱 -直棱柱
直棱柱是指侧棱垂直于底面的棱柱。作为构成物体的基本几何形体之一,它有很多独特的性质。
展开图
展开图是指空间形体的表面在平面上摊平后得到的图形。直棱柱展开图的绘制对于模型和空心工件的制作有重要作用。
直棱柱展开图的特点
棱柱
如果沿着直棱柱的两个底面和一条棱线将其展开,则会得到右图所示的展开图。
从图中不难得出棱柱展开图的特点:
(1)棱柱的所有侧面都是矩形且都有一边相等。
(2)棱柱体两个底面的边展开后形成两条平行且相等的线段,与棱柱所有棱线垂直。
直棱柱展开图绘制方法
棱柱
根据直棱柱展开图的特点,可以绘制出直棱柱的展开图。
1.找出棱柱体的两个底面,依据透视原理画出它们其中一个的真形。
2.确定棱柱体的高度,过棱柱体底面的最高水平边的端点向上作两条与棱柱体的高度等长的线段。
3.向两边延长棱柱体底面的最高水平边,过两条垂线段的较高端点作一条直线,构成一组平行线。在靠下的直线上依次截取与棱柱体底面各边(底面的最高水平边除外)等长的线段(注意对应关系),得到几个直线上的点,过这些点向上作垂线,交上面的水平直线于几点上。棱柱体的侧面就画好了。
4.将各条垂线段的中点找出,过这些点作一条直线,以这条直线为对称轴作棱柱体底面的轴对称图形。
侧面积
如果直棱柱的底面周长是c,高是h,那么它的侧面积是S直棱柱侧=ch。如图所示,若直五棱柱ABCDE-A′B′C′D′E′的底面周长为c,高为h,则S直五棱柱侧=ch。
斜棱柱的侧面积
如果斜棱柱的侧棱长是l,直截面的周长是c1,那么它的侧面积是S斜棱柱侧=c1l。
棱柱的体积
棱柱的体积公式: (s为底面积,h为高)
在搞清上面的知识基础上,还须掌握以下几点:
1)棱柱的截面主要是对角面和平行于底面的截面,学习时应注意掌握它们的性质,其余各种截面应从其位置及形状去分析考虑。
2)求棱柱的侧面积时,应注意它是求各侧面面积的和,而不是指求某一个侧面的面积。
①直棱柱的侧面积是将棱柱的侧面展开后推导得出公式,使用时不应死记公式,而应从侧面形状来分析求取。
②斜棱柱的侧面积可分析侧面形状逐个求得,也可用直截面周长与侧棱长的乘积。
3)我们知道长方体的体积是它的底面积乘以高,一般的,棱柱的体积等于它的底面积乘以高。圆柱的体积也等于底面积乘以高。柱体(棱柱、圆柱)的体积公式是V柱体=S・h。其中S是柱体的底面积、h是柱体的高。
 爱华网
爱华网