阻尼系数是指电器系统的额定负载阻抗与该系统电驱动源的输出阻抗的比值。阻尼系数大则表示该驱动源的输出阻抗远远小于额定负载阻抗。阻尼系数间可间接的表示驱动设备控制负载反作用的能力。阻尼系数大的系统,就相当于设备的输出端是一个内阻很小的近似恒压源,负载的反作用感应电压将在该内阻的作用下被短路,形成较大的短路电流,这种短路电流反过来又抑制了负载的寄生反作用力,最终趋于稳定。阻尼系数多用于电声系统的电驱动源(功放)与作为负载的换能设备(音箱)之间的电阻尼分析计算。在其它领域也有应用。在电声系统中,合理的阻尼系数有助于改善声音的干润程度,但是不同的使用对象,不同的环境和不同的音乐内容,会有不同的合理阻尼系数,不能简单认为阻尼系数越大越好或越小越好,这种合理的阻尼系数也可理解为合理的阻抗匹配。
阻尼系数_阻尼系数 -定义
阻尼系数:阻尼系数(Damping Factor)是指放大器的额定负载(扬声器)阻抗与功率放大器实际阻抗的比值。阻尼系数大表示功率放大器的输出电阻小,阻尼系数是放大器在信号消失后控制扬声器锥体运动的能力。具有高阻尼系数的放大器,对于扬声器更象一个短路,在信号终止时能减小其振动。 功率放大器的输出阻抗会直接影响扬声器系统的低频Q值,从而影响系统的低频特性。扬声器系统的Q值不宜过高,一般在0.5~l范围内较好,功率放大器的输出阻抗是使低频Q值上升的因素,所以一般希望功率放大器的输出阻抗小、阻尼系数大为好。阻尼系数一般在几十到几百之间,优质专业功率放大器的阻尼系数可高达200以上。
一个二阶以及二阶以上的系统,在系统运动过程中系统的内在能量的消耗有两种情况:
系统能量保持不变;
系统能量逐渐减少;
阻尼系数就是表征能量减少这一特性的。
阻尼系数
阻尼系数KD定义为:KD=功放额定输出阻抗(等于音箱额定阻抗)/功放输出内阻。由于功放输出内阻实际上已成为音箱的电阻尼器件,KD值便决定了音箱所受的电阻尼量。KD值越大,电阻尼量越重,当然功放的KD值并不是越大越好,KD值过大会使音箱电阻尼过重,以至使脉冲前沿建立时间增长,降低瞬态响应指标。因此在选取功放时不应片面追求大的KD值。作为家用高保真功放阻尼系数有一个经验值可供参考,最低要求:晶体管功放KD值大于或等于40,电子管功放KD值大于或等于6
。
阻尼系数_阻尼系数 -阻尼系数解析
扩音机的规格之一
阻尼系数是扩音机的规格之一,它直接影响扩音机对喇叭的操控性。一般扩音机所提供的阻尼系数数据,都只公布某一个频段的阻尼系数。
不是越高越好
喇叭与扩音机之间的关系错综复杂,功率与灵敏度的配搭方式只是一个基本,而电流与喇叭之间更是无可捉摸,不能单从规格表上可以判断出来,只能凭经验和用耳去听。除了电流捉摸不到之外,还有一样就是阻尼系数(Damping Factor)。
不同频段会改变
事实大多数扩音机的阻尼系数,在不同频段时都会改变,故所提供的数据也只能作为一个大约指示。有些喇叭需要高的阻尼系数去控制单元的动作,如果配上阻尼不足的扩音机,单元会有失控的情况,出现多余的谐震及音讯损失。
反过来说
如果一对不需高阻尼的喇叭配上高阻尼扩音机,单元由于受到高阻尼的控制,声音会变死实实,音尾会极短。不当的阻尼配搭,会令到一对十分优良的喇叭,变成比鸭寮街出品也不如。
喇叭和扩音机的关系千变万化,切忌“一本通书睇到老”(粤语俗语,睇:”看“的意思),虽然有一定的法则,但都要有心理准备,随时有意外的惊喜发生,所以要客观去对待两者之间的配搭。
想知道某扩音机配某喇叭是否合拍,除了问有丰富经验的朋友之外,最好是自己去听多一些不同的组合配搭。
阻尼系数_阻尼系数 -阻尼系数匹配
阻尼系数KD定义
阻尼系数KD定义为KD=功放额定输出阻抗(等于音箱额定阻抗)/功放输出内阻。由于功放、输出内阻实际上已成为音箱的电阻尼器件,KD值便决定了音箱所受的电阻尼量。KD值越大,电阻尼越重。功放的KD值并不是越大越好,KD值过大会使音箱电阻尼过重,以至使脉冲前沿建立时间增长,降低瞬态响应指标。因此在选取功放时不应片面追求大的KD值。作为家用高保真功放,阻尼系灵敏有一个经验值可供参考;晶体管功放KD值大于或等于40,电子管功放KD值大于或等于6。保证放音的稳态特性与瞬态特性良好的基本条件,应注意音箱的等效力学品质因素(Qm)与放大器阻尼系数(KD)的配合,这种配合需将音箱的馈线作音响系统整体的一部分来考虑。音箱馈线的功率损失小0.5dB(约12%)即可达到这种配合。
一般来说,线越粗越好,最好是双线分音,但是要求音箱是有双线分音的分频器,一般中高档的都有4个接线座,上下的2个负极是独立的,不连接在一起的,连接在一起的是假冒的。
不成文的认同
在老烧友中,有一个不成文的认同,就是功放的输出功率应该至少是音箱价格的1.5-2倍,越是高档的产品这个比例就越高。换句话说,在配套上,宁可“大马拉小车”,不可“小马拉大车”。这是因为往往越是高档的音箱,一个只能发挥70%水平的高档产品,往往反不如一个发挥100%的低档产品。不过放到多媒体产品上,情况就倒了过来,越是高档的产品,其功放占整套产品成本的比例往往越低。有些产品几乎要用4000元档次的功放推其裸箱,才能将单元的水平发挥个八九不离十,但配的仅仅是个最多值100元的功放。有些多媒体发烧友还往往看好这些产品,其实,如果不考虑摩机的话(当然,对于摩机来说,这样的产品是最佳的,因为摩电路是可行的,摩单元,对大多数人是完全不可行的),这样的产品不管在实际发挥的效果上,还是作为商品的设计上(特别是这一点),都是不理想也不合理的。说到底,还是文章的主旨――合理搭配,在功放上下功夫,用差单元当然是不好的,但反过来,将成本全花在单元上,配一个仅仅是刚刚能用的功放同样是不可行的。单元虽然是多媒体音箱最重要的部件,但决不是单元好就是好箱子。
阻尼系数_阻尼系数 -力学阻尼系数
阻尼模型
结构阻尼是对振动结构所耗散的能量的测量,通常用振动一次的能量耗散率来表示结构阻尼的强弱。典型结构体系的真实阻尼特性是很复杂和难于确定的。近几十年来,人们提出了多种阻尼理论假设,在众多的阻尼理论假设中,用得较多的是两种线性阻尼理论:粘滞阻尼理论和复阻尼理论(滞变阻尼理论)。
粘滞阻尼理论可导出简单的运动方程形式,因此被广泛应用。可是它有一个严重的缺点,即每周能量损失依赖于激励频率。这种依赖关系是与大量试验结果不符的,试验结果表明阻尼力和试验频率几乎是无关的。因此,自然期望消除阻尼力对频率的依赖。这可以用称为滞变阻尼的形式代替粘滞阻尼来实现。滞变阻尼可定义为一种与速度同相而与位移成比例的阻尼力。在考虑阻尼时在弹性模量或刚度系数项前乘以复常数 即可,v为复阻尼系数。复阻尼理论对于一般的结构动力响应来说,计算过程非常复杂,因此,在动力响应分析中,复阻尼理论应用不多,本文限于篇幅,也就不再展开了。
粘滞阻尼理论假定阻尼力与运动速度成正比,通常是用不同频率的阻尼比ζ来表征系统的阻尼:
粘滞阻尼理论最显着的特点在于其阻尼力是直接根据与相对速度成正比的关系给出的,不论是简谐振动或是非简谐振动,都可直接写出系统的运动方程,而且均为线性微分方程,给理论分析带来了很大的方便。
在多自由度系统中采用等效粘滞模态阻尼,阻尼力向量的表达式为
若[C」可以通过模态向量正交化为对角矩阵时,则称为正交阻尼或比例阻尼。反之,则称之为非正交阻尼。因为无阻尼振型对质量和刚度都是正交的。所以为方便计算,通常假设振型对阻尼矩阵也是正交的。最简单的方法是使其与质量矩阵或者刚度矩阵成比例。或许这就是比例阻尼这一名称的来历。正交阻尼原则上适用于阻尼特性分布比较均匀的工程结构。但是,对于多于一种材料组成的结构,由于不同材料在结构的不同部分提供的能量损失机制差别很大,所以阻尼力的分布将与惯性力和弹性力的分布不同;换句话说,这种情况导致的阻尼将不是成比例的。
Rayleigh阻尼模型是广泛采用的一种正交阻尼模型,其数学表达式如下:
C=a0M+a1K (2)
式中, a0和a1称为Rayleigh阻尼常数。
在Rayleigh阻尼模型下,各阶阻尼比可表示为
式中ζi称为第i阶振型的模态阻尼比,因此若已知任意两阶振型的阻尼比ζi和ζj,则可定出阻尼常数
确定了a0和al之后,即可确定出各阶振型的模态阻尼比,并确定阻尼矩阵。
阻尼选取对实际抗震分析的影响
目前,桥梁地震反应分析一般以直接积分的时程分析方法为主。其阻尼模型取Rayleigh阻尼模型,并以主塔或主梁的两个较低阶振型频率ωi和ωj对应的阻尼比作为ζi和ζj,接式(3)和式(4) 求出其余各阶频率的阻尼比,并求出阻尼矩阵代入动力方程,用直接积分的方法求解动力方程。这样处理阻尼虽然非常简单,但也产生了以下两个不可忽视的问题:
(1)如前所述,Rayleigh阻尼作为一种正交阻尼,适用于阻尼特性分布非常均匀的工程结构。但是大跨桥梁一般来说都不能算作非常均匀的结构。例如,为了提高桥梁的跨越能力,主梁一般采用钢箱梁或钢混叠合梁,而主塔和边墩则采用钢筋混凝土材料,两者的阻尼特性相差比较大。即使主梁材料特性与主塔差不多,大跨桥梁由于抗风和抗震的要求,经常会在桥梁结构的某些部位加有人工阻尼装置,比如桥墩上安放高阻尼的抗震支座、桥塔上安放控制振动的装置TMD等,这都会产生摩擦阻尼或集中阻尼从而造成阻尼特性的不均匀分布。这样的阻尼均匀性前提得不到满足的情况下,仍按照 Rayleigh阻尼模型去计算各阶振型对应的阻尼比势必会造成除ωi和ωj两阶之外其他各阶振型阻尼比与真实值有或多或少的差别。
(2)根据同济大学土木防灾国家重点实验室对国内几十座大跨桥梁进行抗震分析后总结的经验,边墩。辅助墩等部位是大跨桥梁抗震设施的重点。但是采用Rayleigh阻尼模型时,用于计算其他各阶振型阻尼比的ωi和ωj一般取的是较低阶的振型,而边墩辅助墩的振动一般都发生在高阶振型。根据Rayleigh阻尼模型图,可以看出离ωi和ωj越远的振型,其阻尼比就越不准,而且随着图上阻尼比按频率增加的速度越来越快,边墩部分振动频率对应的阻尼比比实际值往往偏大,从这一点讲会导致边墩部分反应的计算结果偏于不安全。
一些桥梁抗震研究人员已经注意到了以上两个问题,他们采取的措施是根据分析的部位不断变换所选择的ωi和ωj,比如计算桥塔的纵向地震反应时就选择对桥塔的纵向反应起主要作用的两阶频率作为ωi和ωj,来计算其它各阶阻尼比,计算其它地震反应时也依此类推。这样就需要分析人员不断的重复选择。和约和进行时程计算,十分繁琐。
解决方法
由以上论述,我们已经了解到阻尼是一个非常复杂的问题,仅仅依靠Rayleigh阻尼模型,会对大跨桥梁尤其是边墩辅助墩等部位的地震反应分析出现不应有的误差。因此,我们尝试寻找一种既不过分繁琐又比较准确的方法。
在前面的论述中,我们发现阻尼比是反应阻尼的一个方便而有效的量,它把阻尼特性和振型频率联系起来,使得动力方程分析起来更为简单,而且阻尼比可以通过桥梁实测测出。
如果我们直接指定对桥塔。主梁、边墩等重要部位反应起主要作用的一些振型频率的阻尼比,而对其余各阶振型频率的阻尼比采用线性内插的方法确定,这样做也可以形成阻尼比矩阵。由于我们通过以前的工程实例发现结构各部位的反应来说少数几阶振型的贡献最为显着(这些振型的贡献占到70%~ 80%,甚至更多),因此,这样做能够保证计算的正确性,而且并不繁琐,此对,以实测试验数据作为基础,更增加了其准确性。同济大学桥梁系近十几年来,通过为国内几十座大型桥梁进行竣工检测、成桥检测积累了大量的阻尼实测资料,并有研究人员准备把这些阻尼资料整理形成桥梁阻尼数据库。有了这些数据资料为基础,通过指定主要振型频率阻尼比,来计算结构动力反应是行得通的,并且结合下面的振型叠加法,会使计算更加简便。
阻尼系数_阻尼系数 -受迫振动阻尼系数公式
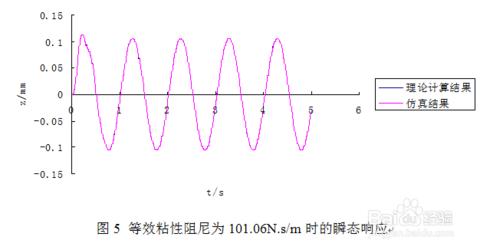
x = exp(-at)*A*cos(bt + phi)里exp自对数底指数函数abAphi 由阻尼劲度系数滑块质量及初状态决定
阻尼系数_阻尼系数 -常用材料阻尼系数
纯铝
:0.00002~0.002
钢
:0.001~0.008
铅
:0.008~0.014
铸铁
:0.003~0.03
天橡胶
:0.1~0.3
硬橡胶
:1.0
玻璃
:0.0006~0.002
混凝土
:0.01~0.06
 爱华网
爱华网