发布时间:2024年11月06日 14:31:22分享人:黑夜王子高泽文来源:互联网9
切比雪夫多项式是与棣美弗定理有关,以递归方式定义的一系列正交多项式序列。
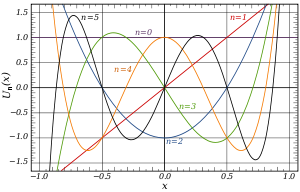
切比雪夫多项式是与棣美弗定理有关,以递归方式定义的一系列正交多项式序列。 通常,第一类切比雪夫多项式以符号Tn表示, 第二类切比雪夫多项式用Un表示。切比雪夫多项式 Tn 或 Un 代表 n 阶多项式。
切比雪夫多项式在逼近理论中有重要的应用。这是因为第一类切比雪夫多项式的根(被称为切比雪夫节点)可以用于多项式插值。相应的插值多项式能最大限度地降低龙格现象,并且提供多项式在连续函数的最佳一致逼近。
在微分方程的研究中,数学家提出切比雪夫微分方程
和
基本性质
对每个非负整数n, Tn(x) 和 Un(x) 都为 n次多项式。 并且当n为偶(奇)数时,它们是关于x 的偶(奇)函数, 在写成关于x的多项式时只有偶(奇)次项。
按切比雪夫多项式的展开式
一个N 次多项式按切比雪夫多项式的展开式为如下:
多项式按切比雪夫多项式的展开可以用 Clenshaw 递推公式计算。
第一类切比雪夫多项式由以下递推关系确定
也可以用母函数表示
第二类切比雪夫多项式由以下递推关系给出
此时母函数为
爱华网本文地址 » http://www.413yy.cn/a/8103470103/110168.html
更多阅读
一、学情分析新课标中指出“小学数学教学必须从学生的生活实际出发,设计富有情趣和意义的活动,使他们从周围熟悉的事物中学习数学,运用数学。”其实就是让学生带着已有的生活经验、认知经验进入课堂,参与学习。在认知经验中,学生已经理

在昔年一个充满了暴力邪恶动乱的时代里,江湖中突然有一种飞刀出现了。没有人知道它的形状和式样,也没有人能够形容它的力量和速度。这就是“小李飞刀”。在今日动荡不安的欧洲足坛,也突然出现了这样一位前锋。他的传奇故事就像童话中的

原文地址:休·海夫纳+了不起的盖茨比作者:北京书香教育1、休·海夫纳(Hugh Hefner,原名:Hugh Marston Hefner,1926年4月9日-)是一位美国实业家,杂志出版商。休·海夫纳是世界著名色情杂志《花花公子》的创刊人及主编,以及花花公子企业的首席

每个球队都有那么件球衣,让人远观羡之而不敢亵玩,生怕背负不起那么多传承。比如,克鲁伊夫留给荷兰的14号,凝聚贝利、济科、里瓦尔多神魂的巴西10号,阿根廷那件被马拉多纳阴影覆盖到几乎要被退役的10号,意大利(或AC米兰)被马尔蒂尼和巴雷西神

出租车几何或曼哈顿距离(Manhattan Distance)是由十九世纪的赫尔曼·闵可夫斯基所创词汇,是种使用在几何度量空间的几何学用语,用以标明两个点上在标准坐标系上的绝对轴距总和。图中红线代表曼哈顿距离,绿色代表欧氏距离,也就是直线距离,而

 爱华网
爱华网



