卡瓦列里_卡瓦列里原理 -主要内容
如果两个平面图形夹在同一对平行线之间，并且为任何平行于这两条平行线的直线所截时截得的线段都相等，那么这两个图形的面积相等；如果每条直线(平行于上述两条平行线的)为两个图形所截得的线段的长度都有相同的比，则两个图形的面积也成相同的比．
卡瓦列里_卡瓦列里原理 -相关解释
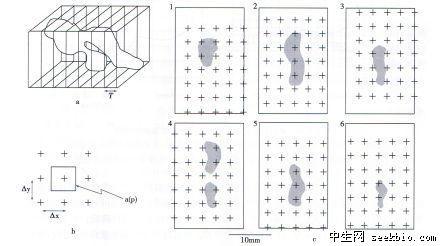
类似地，在空间，如果两个立体图形夹在两个平行平面之间，并且为任何平行于这两个平行平面的平面所截时截得的平面片的面积都相等，那么这两个立体图形的体积相等；如果截两个立体所得的两组截面中，每个给定平面所截得的两个不同组的截面的面积都有相同的比例，则这两个立体的体积也成相同的比．
从现代分析学的观点看，这个原理所断定的实际上是：如果被积函数相等，而且积分限也相等，那么这两个积分相等；被积函数中的常数作为一个因子可以提到积分号外面而不改变积分的值．
这一原理在西方是由卡瓦列里提出的，此后在数学中得到相当广泛的应用．西方便称之为卡瓦列里原理．在中国古代，三国时的刘徽和南北朝时的祖冲之父子曾考虑过相同的原理，公元5―6世纪的祖
真正的万人斩!契卡刽子手瓦西里28天枪杀7千多人 钢蛋超人 今天12:22:13 收藏 分享> 23 5703今天我们来讲点压抑的内容。不知大家听说过没听说过这个词。 我们今天就来聊聊这个由列宁时代建立的血腥组织的往事。[ 转自铁血社区 ht
再一次阅读托尔斯泰的长篇小说《安娜.卡列尼娜》，对其中关于跳舞会的描写倍感亲切。从舞会的准备到舞会的盛大场面以及各个人物的心理活动，在大文豪的笔下惟妙惟肖的展现在我们眼前。在忘我的身临其境的阅读中，小说描写的跳舞会里的许
是谁杀死了安娜——重读托尔斯泰《安娜·卡列尼娜》“……他道了声歉，往车厢里走，但又觉得想再看她一眼。倒不是因为她非常美丽、身姿优美素雅，而是因为她从身旁走过时，脸上有一种特别温柔亲切的表情。他回眼望她时，恰好她也转过头来…
卡瓦打捞筒（Overshot）是非常常用的打捞工具，主要打捞对象为外表光滑的管状落鱼，属于外捞型（即抓牢落鱼的外表面）打捞工具。简介：卡瓦打捞筒由上接头、筒体、引鞋、卡瓦、控制环组成，另外还有A型盘根、R型盘根以及O型密封圈等组成。抓捞落鱼
卢卡斯.雷瓦，一个并不是太有名气的足球运动员，但对于现在的这只利物浦来说，他是球队中不可或缺的人物。5年前的那个夏天，拉法将卢卡斯带到了梅尔伍德，那个时候的卢卡斯刚刚在解放者杯的比赛中，输给了阿根廷的老大哥里克尔梅。并且出现了
爱华网