拉格朗日中值定理 拉格朗日中值定理 拉格朗日中值定理-定律定义，拉格朗日中值定理

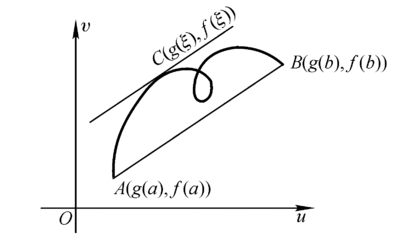
拉格朗日中值定理又称拉氏定理，是微分学中的基本定理之一，它反映了可导函数在闭区间上的整体的平均变化率与区间内某点的局部变化率的关系。拉格朗日中值定理是罗尔中值定理的推广，同时也是柯西中值定理的特殊情形，是泰勒公式的弱形式（一阶展开）。法国数学家拉格朗日于1778年在其着作《解析函数论》的第六章提出了该定理，并进行了初步证明，因此人们将该定理命名为拉格朗日中值定理。

拉格朗日中值定理_拉格朗日中值定理 -定律定义

定理表述

如果函数

满足：

（1）在闭区间

上连续；

（2）在开区间

内可导；

那么在开区间

内至少有一点

使等式

成立。

其他形式

设

是闭区间

内一点

为区间内的另一点

，则定理在

或在区间

可表示为

此式称为有限增量公式。

拉格朗日中值定理_拉格朗日中值定理 -数学推导

辅助函数法：

已知

在闭区间

上连续，在开区间

内可导，

构造辅助函数

验证可得

又因为函数

在闭区间

上连续在开区间

内可导，

且

根据罗尔定理可知在

内至少有一点

是

即

由此可得

即

定理证毕。

拉格朗日中值定理_拉格朗日中值定理 -定理

拉格朗日中值定理又称拉氏定理，是罗尔中值定理的推广，同时也是柯西中值定理的特殊情形。如果函数f(x)在(a，b)上可导，[a,b]上连续，则必有一ξ∈(a,b)，使得f'(ξ)*(b-a)=f(b)-f(a) 拉格朗日中值定理的几何意义。在(a，b)上可导，[a,b]上连续是拉格朗日中值定理成立的充分条件。理解――这个定理说的是什么1.在满足定理条件的前提下，函数f(x)上必有【一点的切线】与【f（x）在x=a，b处对应的两点（(a,f(a))和(b,f(b))点的连线平行）。f'(ξ)=[f(b)-f(a)]/（b-a），等号后为x=a，b对应两点的连线斜率，等号前为f(x)上一点的导数的值，也就是f(x)上一点的斜率，两斜率相等，两线平行。这是几何上的理解方式。2.我们将f(x)函数求导，得到f'(x)，众所周知f'(x)函数记录的其实就是【f(x)函数在每一个瞬间的变化状态】。即，在x=x1这一瞬间f（x）进行了程度为f'(x1)的变化，在x=x2这一瞬间f（x）进行了程度为f'(x2)的变化……。函数由f(a)变化到f(b)的过程，其实就是f'(x)函数在(a，b)区间中记录的变化状态的依次累加，就是对f'(x)函数在(a，b)区间的值进行积分的过程。那么，将这一过程中所有的变化状态的值一起取一个平均，这个平均值的数值一定在f'(x)的某一点上出现过（即f'(ξ)），因为f(x)连续，则其导数也连续。这个平均值乘上变化的区间（a到b）的长度 就等于这个 变化的变化量【】。即所谓的必有一，使f'(ξ)*(b-a)=f(b)-f(a)。即，【a，b区间上f（x）函数的变化量】=【a，b区间内f（x）函数变化状态的平均值乘以区间长度】。这是代数理解方式。

拉格朗日中值定理_拉格朗日中值定理 -其它形式

拉格朗日中值定理的几何意义令f(x)为y，则该公式可写成△y=f'(x+θ△x)*△x (0

拉格朗日中值定理_拉格朗日中值定理 -定理内容

若函数f(x)在区间[a,b]满足以下条件：(1)在[a,b]连续(2)在(a,b)可导则在(a,b)中至少存在一点f'(c)=[f(b)-f(a)]/(b-a) a

拉格朗日中值定理_拉格朗日中值定理 -证明

证明:把定理里面的c换成x再不定积分得原函数f(x)={[f(b)-f(a)]/(b-a)}x.做辅助函数

易证明此函数在该区间满足条件:1.g(a)=g(b)=0;2.g(x)在[a,b]连续;3.g(x)在(a,b)可导.此即罗尔定理条件,由罗尔定理条件即证

拉格朗日中值定理_拉格朗日中值定理 -几何意义

若连续曲线y=f(x)在A(a,f(a)),B(b,f(b))两点间的每一点处都有不垂直于x轴的切线,则曲线在A,B间至少存在1点P(c,f(c)),使得该曲线在P点的切线与割线AB平行。

拉格朗日中值定理_拉格朗日中值定理 -发展简史

人们对拉格朗日中值定理的认识可以上溯到公元前古希腊时代。古希腊数学家在几何研究中得到如下结论：“过抛物线弓形的顶点的切线必平行于抛物线弓形的底”。这正是拉格朗日定理的特殊情况，古希腊数学家阿基米德正是巧妙地利用这一结论，求出抛物弓形的面积.。

意大利卡瓦列里在《不可分量几何学》(1635年)的卷一中给出处理平面和立体图形切线的有趣引理，其中引理3基于几何的观点也叙述了同样一个事实：曲线段上必有一点的切线平行于曲线的弦。这是几何形式的微分中值定理，被人们称为卡瓦列里定理。该定理是拉格朗日中值定理在几何学中的表达形式。

1797年，法国数学家拉格朗日在《解析函数论》一书中首先给出了拉格朗日定理，他给出的定理的最初形式是：“函数

在

与

之间连续，

在

与

之间有最小值

与最大值

，则

必取

与

之间的一个值。”拉格朗日给出最初的证明，但证明并不严格，他给的条件比现在的条件要强，他要求函数

在闭区间上具有连续导数

，并且他所用的连续也是直观的，而不是抽象的。

十九世纪初，在微积分严格化运动中，柯西给出了拉格朗日中值定理的严格证明，在《无穷小计算教程概论》中，柯西证明了”如果导数

在闭区间

上连续，则必存在一点

，使得

。 ”柯西又在《微分计算教程》中将拉格朗日中值定理推广为柯西中值定理。

现代形式的拉格朗日中值定理是由法国数学家博（O.Bonnet）给出的，他不是利用导数

的连续性，而是利用罗尔定理对拉格朗日中值定理进行了重新证明。

拉格朗日中值定理_拉格朗日中值定理 -定理意义

拉格朗日中值定理是微分中值定理的核心，其他中值定理是拉格朗日中值定理的特殊情况和推广，它是微分学应用的桥梁，在理论和实际中具有极高的研究价值。

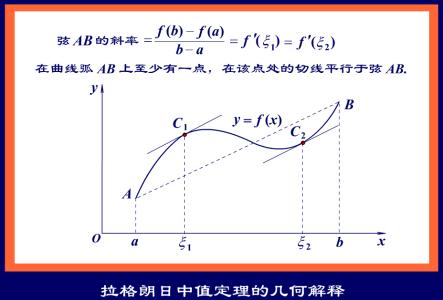
几何意义：

若连续曲线在

两点间的每一点处都有不垂直于x轴的切线，则曲线在A，B间至少存在1点

，使得该曲线在P点的切线与割线AB平行。

运动学意义：对于曲线运动在任意一个运动过程中至少存在一个位置（或一个时刻）的瞬时速率等于这个过程中的平均速率。

拉格朗日中值定理在柯西的微积分理论系统中占有重要的地位。可利用拉格朗日中值定理对洛必达法则进行严格的证明，并研究泰勒公式的余项。从柯西起，微分中值定理就成为研究函数的重要工具和微分学的重要组成部分。

爱华网本文地址 » http://www.413yy.cn/a/8103420103/93182.html