表示时用“cot+角度”,如:30°的余切表示为cot30°;角A的余切表示为cotA 旧用ctgA来表示余切,至今仍在使用,和cotA是一样的。(注:现在已经不常用了)任意角中边上除顶点外的任一点的横坐标除以该点的非零纵坐标,角的顶点与平面直角坐标系的原点重合,而该角的始边则与正x轴重合简单点理解:直角三角形任意一锐角的邻边和对边的比,叫做该锐角的余切。
余切函数_余切 -概述
表示时用“cot+角度”,如:30°的余切表示为cot30°;角A的余切表示为cotA旧用ctgA来表示余切,至今仍在使用,和cotA是一样的。(注:现在已经不常用
余切函数了)
任意角终边上除顶点外的任一点的横坐标除以该点的非零纵坐标,角的顶点与平面直角坐标系的原点重合,而该角的始边则与正x轴重合
简单点理解:直角三角形任意一锐角的邻边和对边的比,叫做该锐角的余切。
假设∠A的对边为a、邻边为b,那么:
cot A= b/a(即邻边比对边)
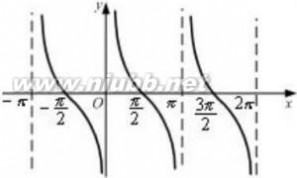
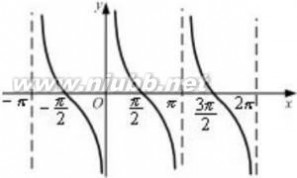
右图为余切函数图像。
余切函数_余切 -余切的性质
1.与正切互为倒数2.单调递减
3.奇函数
4.值域R
余切函数_余切 -相关公式
和的关系
1+cot^2α=csc^2α
积的关系
cotα=cosα×cscα
tanα ・cotα=1商的关系
cosα/sinα=cotα=cscα/secα
由泰勒级数得出cotx=1/tanx=[ie^(ix)+ie^(-ix)]/[e^(ix)-e^(-ix)]
和角公式
cot(α+β)=(cotαcotβ-1)/(cotα+cotβ)
cot(α-β)=(cotαcotβ+1)/(cotβ-cotα)余切函数_余切 -余切是混沌的
“余切序列”是蝴蝶效应的一个典型例子。你看,以下三个数列每一项都是前一项的余切;初值分别为1、1.00001、1.00001,但是从第10项开始,三个数列开始形成巨大的分歧。这就是混沌的数列,经过足够多项后,得到的数字完全可以看作是随机的,混沌的。a[n+1]=cot(a[n])??甲乙丙11.000011.00010.6420926160.6420784930.6419513971.3372531781.3372925561.3376470060.2378838770.2378422710.2374678014.1241363324.1248857294.1316421090.6670279030.665945620.6562364341.2699574741.2727891481.298546250.3102556110.307154080.2791820713.1190604633.1526604993.488344037-44.3734379690.348130062.767389601-2.424894313-1.056234059-2.5464313981.147785023-0.5653638021.4769811640.45018926-1.5761759160.0940913672.0691574070.00537964110.5965853-0.544176342185.88421660.421601998-1.6525623991.7057482612.2296772570.081948782-0.135777195-0.77431333812.17541547-7.31969225-1.02241908-2.42617226-0.59169349-0.6108746881.150750903-1.48807061-1.4281192840.44662703-0.082914948-0.1436531382.088110796-12.03290058-6.913261967-0.5690013761.693228262-1.371305422
 爱华网
爱华网