高通滤波电路是将低通滤波电路和高通滤波电路进行不同组合,可获得带通滤波电路和带阻滤波电路。
高通滤波器_高通滤波电路 -实验内容
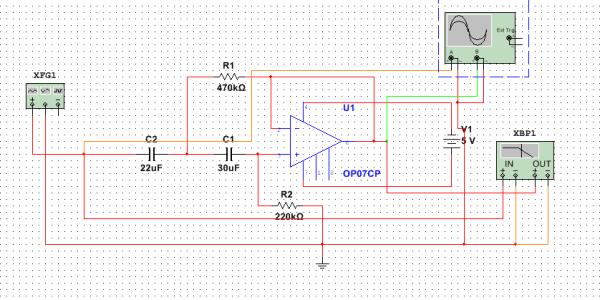
1.一阶有源高通滤波电路
.
A、R1、Rf――同相比例运算电路,Af=(1+RfR1)=9
R、C――一阶高通滤波电路,截止频率
f0=12πRC=12×3.14×8×103×1×10?9=19.904kHZ
(1)观察频率特性
点击工具栏“显示图形”按钮,观察幅频特性。
(2)测量截止频率f0
打开波特图仪面板,连续点击“→”,测量通带内放大倍数(db),其值为19.08db;点击“→”,使放大倍数下降3db,测量截止频率。
测量值:f0=19.96kHz
计算值:f0=19.904kHZ
(3)改变输入信号频率f,分别观察f>>f0、f<<f0时的输出波形。
结论:
f>>f0时,输入信号频率f变化,幅值不变,则输出幅值不变;
f<<f0时,输入信号频率f变化,幅值不变,则输出幅值随输入信号频率f的下降而下降。
电路具有高通特性。
仿真实验演示
高通滤波器_高通滤波电路 -幅频特性
高通滤波电路的幅频特性曲线如下图所示:
高通滤波器_高通滤波电路 -二阶有源高通滤波电路
设置R1=1kΩ,Rf=8kΩ,R=8kΩ,C=1nF。
.
(1)观察二阶有源高通滤波电路频率特性,与一阶有源高通滤波电路进行比较。
结论:
阻带内放大倍数衰减更快。
(2)设置R1=10kΩ,Rf=10kΩ,将R1接至输出端,得到改进型二阶有源高通滤波电路,观察其频率特性,与二阶有源高通滤波电路进行比较。
改变Rf分别为5kΩ、10kΩ、15kΩ和20kΩ,对应得Q值分别为0.5、1、2、∞,观察幅频特性。
结论:
1)在f=f0处,放大倍数下降得少,阻带内放大倍数衰减更快。
2)Q=1时幅频特性较好,接近理想特性。
高通滤波器_高通滤波电路 -高通滤波器的应用
这样的滤波器能够把高频率的声音引导至专用高音喇叭(tweeter),并阻止可能干
 爱华网
爱华网