《初二几何证明题》证明书
初二几何证明题1.
已知:如图,在△ABC中,AD⊥BC,垂足为D,BE⊥AC,垂足为E。M为AB中点,联结ME,MD、ED
求证:角EMD=2角DAC
证明:
∵M为AB边的中点,AD⊥BC, BE⊥AC,∴ MD=ME=MA=MB(斜边上的中线=斜边的一半)∴△MED为等腰三角形∵ME=MA
∴∠MAE=∠MEA∴∠BME=2∠MAE∵MD=MA(散文阅读:www.www.AihuAu.com.net )
∴∠MAD=∠MDA, ∴∠BMD=2∠MAD, ∵∠EMD=∠BME-∠BMD=2∠MAE-2∠MAD=2∠DAC
2.
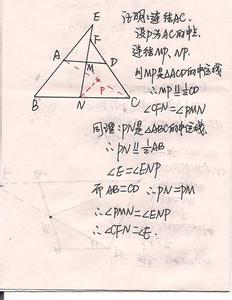
如图,已知四边形ABCD中,AD=BC,E、F分别是AB、CD中点,AD、 BC的延长线与EF的延长线交于点H、D
求证:∠AHE=∠BGE
证明:连接AC,作EM‖AD交AC于M,连接MF.如下图:
∵E是CD的中点,且EM‖AD,
∴EM=1/2AD,M是AC的中点,又因为F是AB的中点
∴MF‖BC,且MF=1/2BC.
∵AD=BC,
∴EM=MF,三角形MEF为等腰三角形,即∠MEF=∠MFE.
∵EM‖AH,∴∠MEF=∠AHF
∵FM‖BG,∴∠MFE=∠BGF
∴∠AHF=∠BGF.
3.
写出“等腰三角形两底角的平分线相等”的逆命题,并证明它是一个真命题
这是经典问题,证明方法有很多种,对于初二而言,
下面的反证法应该可以接受
如图,已知BD平分∠ABC,CE平分∠ACB,BD=CE,求证:AB=AC
证明:
BD平分∠ABC==>BE/AE=BC/AC==>BE/AB=BC/(BC+AC)
==>BE=AB*BC/(BC+AC)
同理:CD=AC*BC/(BC+AB)
假设AB≠AC,不妨设AB>AC.....(*)
AB>AC==>BC+ACAC*BC
==>AB*AB/(BC+AC)>AC*BC/(BC+AB)
==>BE>CD
AB>AC==>∠ACB>∠ABC
∠BEC=∠A+∠ACB/2,∠BDC=∠A+∠ABC/2
==>∠BEC>∠BDC
过B作CE平行线,过C作AB平行线,交于F,连DF
则BECF为平行四边形==>∠BFC=∠BEC>∠BDC.....(1)
BF=CE=BD==>∠BDF=∠BFD
CF=BE>CD==>∠CDF>∠CFD
==>∠BDF+∠CDF>∠BFD+∠CFD==>∠BDC>∠BFC...(2)
(1)(2)矛盾,从而假设(*)不成立
所以AB=AC。
2、
两地角的平分线相等,为等腰三角形
作三角形ABC,CD,BE为角C,B的角平分线,交于AB,BE.两平分线交点为O
连结DE,即DE平行BC,所以三角形DOC与COB相似。
有DO/DC=EO/EB,又EB=DC所以DO=EO,三角形COB为等腰
又角ODE=OCB=OED=OBC
又因为BE和DC是叫平分线,所以容易得出角C=角B(这个打出来太麻烦了),即ABC为等腰。
 爱华网
爱华网



