拉马努金印度现代数学家。1887年12月22日生于印度南方坦焦尔区的埃罗德,1920年4月26日卒于马德拉斯附近。幼年时即显示出数学才能,家境贫困,1904年获奖学金入贡伯戈讷姆学院,潜心研习数学。
标题:拉马努金是谁?拉马努金函数介绍
网址:http://u.www.AihuAu.com.net/subject/1010770.html
沙发回目录
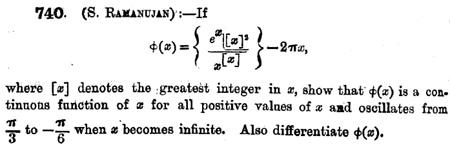
Re:拉马努金个人履历
捧心西子 | 2013-01-05 17:08
拉马努金(泰米尔文:????????? ?????????,拉丁字母转写:Srinivasa Aiyangar Ramanujan)(1887年12月22日-1920年4月26日),印度数学家。
1914年在G.H.哈代的帮助下进入剑桥大学,和哈代共同研究。数年间成果累累。在堆垒数论特别是整数分拆方面有突出贡献。此外在椭圆函数、超几何函数、发散级数等领域也有不少工作。他有较强的直觉洞察力,常能预见某些数学的结论,日后有许多得到了证实。1918年被选为英国皇家学会会员。1919年因患肺结核病被迫回到家乡,次年病逝。
主要贡献:椭圆函数、超几何函数、发散级数、堆垒数论
板凳回目录Re:拉马努金天才之路
捧心西子 | 2013-01-05 17:08
天才不可培养,也不易发现
一般来说天才大致可分为两种,一种是“才思敏捷型”,象棋大师就属此类;另一种是“思想深沉型”,爱因斯坦无疑是其代表。无论哪一种,首先必须是成功者才能为人所知,而成功更多地依赖于非智力因素。建立原创性理论的机会并不多,所以换个时代爱因斯坦可能成不了爱因斯坦,海森伯成不了海森伯……这也就是为什么认知心理学一般对科学大师或象棋冠军并不特别感兴趣的原因。
拉马努金就截然不同,似乎比较难以归类。他经常宣称梦中娜玛卡尔女神给他启示,一早醒来就能写下半打子极为夸张的公式,这显然比速算家远为罕见。哈代认为,拉马努金的高超技巧(不妨称之为“数感”),历史上只有欧拉和雅可比才能与之相比。但是自高斯、黎曼、庞加莱以后,崇尚数感的时代渐渐过去,到20世纪布尔巴基结构主义的崛起,数感被彻底埋葬。
所以,拉马努金本不该引起当时的数学家太多的兴趣,然而事实恰恰相反,这是因为,比起前辈他的数感自有独特之处。他没有受过严格的数学训练,却独立发现了3000~4000个公式。写给哈代信中的那部分,显然只是“冰山之一角”。哈代仔细查看了这些在印度时就开始积累的公式,它们通常有高得不可思议的幂次,多重积分、和式或连分数,犹如“言简意赅的警句,一两行之间压缩了极其丰富的数学真理”(卡尼格尔语)。哈代估计大约有2/3是欧洲数学家已经发现的,他感慨道,一个印度人孤独地对抗着欧洲积累百年的智慧。
#4楼回目录Re:拉马努金研究成果
捧心西子 | 2013-01-05 17:09
这些公式写在著名的“笔记本”上。后世许多数学家参与整理、论证后认为,创新的内容不止1/3,加上改进与推广,总的说来约有2/3的公式是新的,都可算是欧洲数学家的疏漏!尤其是其中也有少量错误,这样一来,拉马努金的思维方式更难以捉摸了,从而也就吊足了人们的胃口。所以哈代曾说,如果拉马努金在青少年时期就被发现并进行一些培养,他可能会成为更伟大的数学家。但他就再也不是拉马努金,而是一个欧洲教授了。
20世纪中叶,随着布尔巴基淡出历史舞台,数感又得到了一定的重视。毕竟证明华林猜想与比贝尔巴赫猜想时,“数感”就引起了轰动,尤其是1978年阿佩瑞运用极其娴熟的古典技巧证明 ζ(3)是无理数,被评价为“一个布尔巴基无能为力然而欧拉应该想得到的证明”。显然,对严肃的认知科学研究来说,拉马努金突出的数感比布尔巴基的思考方式有价值得多。目前,研究拉马努金的论文已超过300篇,至今仍无令人满意的结果。
#5楼回目录Re:拉马努金教育意义
捧心西子 | 2013-01-05 17:09
《知无涯者》。天才都不具有普遍性。如今一些“望子成龙”心切的家长和一批关于“天才”
拉马努金传
的书,在对孩子未来的设计方面产生多大误导,实在无法估计。也许这就是《知无涯者》的教育意义所在。在书中卡尼格尔写道,与其说是哈代发现了拉马努金,还不如说是拉马努金发现了哈代。哈代不是说过,一切天才都是自己造就自己。本书译者之一、知名数学家齐民友教授也说,天才是不可培养的,只能是可遇而不可求。这里的“求”除了培养,还可指发现的意思。也就是说,天才不仅是不可培养,也极不容易发现。据说每500个天才要扼杀499个。在哈代之前,拉马努金也曾给霍布森、贝克两位著名数学家写信,结果还不是石沉大海?所以,这方面没有固定的操作程序(比如考试之类)。拉马努金恐怕在一千年里也不会出第二个!
真正要紧的问题在于,一旦发现天才,就要给他创造良好的条件(所以这本书对决策者也有价值)――正如哈代所做的(到处宣传,合作研究,并使拉马努金成为皇家学会成员等)。人才难得,天才更是凤毛麟角,自古天才与天才相知相遇的故事其稀罕程度可想而知,变成佳话也就不足为奇,而主人公来自不同国家和文化背景的,恐怕只能举出哈代与拉马努金的动人例子。
#6楼回目录拉马努金与哈代
捧心西子 | 2013-01-05 17:09
拉马努金与哈代:一段佳话传千古
哈代
《知无涯者》:
发现天才的传奇故事
1913年初的一天,英国数学大师哈代收到了一封奇特的信。信是这样开头的:
“谨自我介绍如下:我是马德拉斯港务信托处的一个职员……我未能按常规念完大学的正规课程,但我在开辟自己的路……本地的数学家说我的结果是‘惊人的’……如果您认为这些定理是有价值的话,请您发表这些结果……”
落款处,是一个素昧平生的印度人的名字――拉马努金。接下去的几张纸,密密麻麻地写满了公式。
通常这类信件的命运只能是废纸篓――那是每个数学家常干的事。但是从8000公里外的南印度寄来的这封信,总让哈代觉得有点蹊跷。他没有把信扔掉,跑到户外活动去了,心头却牵挂着什么。晚上,哈代特地把同事李特尔伍德请来,一道仔细研究一下。
南印度可是个贫穷落后的地方,那儿会出什么人才呢?难道竟然是个剽窃者,不太像,因为有些夸张的公式即便是博学的哈代也感到陌生;是一个妄想者在瞎编乱造?更不可能,因为“有本事造出这类公式的骗子比起数学天才来更为罕见”。经过三个小时的鉴定,他们得出了唯一的结论,这些公式确实出自一位顶尖水平的数学家之手。
深刻影响
这本书给人最深的印象是,卡尼格尔作为一个现代人,能对当时的历史文化背景把握得非常之好(而这正是写好传记的关键),就好像生活在那个时代似的,实属不易。读《知无涯者》,感觉完全像在看一部精彩的纪录片。卡尼格尔首先将我们引向19世纪末的南印度,1887年,拉马努金出生在一个小村庄,他家族的种姓属婆罗门,尽管高贵,但那时已很贫穷。父母都没受过什么高等教育,兄弟姐妹也都很平庸。大概是读到一本数学公式手册,促使他对数学产生了浓厚的兴趣,结果其他课程受到了影响。后来,他结了婚(是包办婚姻),又到马德拉斯打工,生活比较艰难。但总算认识了一些好心人,他们都帮不上大忙,于是有人建议他与国外联系……在那封信出场前,卡尼格尔把镜头切换到剑桥这个庄严的地方,介绍另一位天才哈代。包括精英们的学术聚会,哈代如何反对陈腐的Tripos制度等,都写得很有味。由于哈代的邀请,拉马努金颇费周折到了英国。他工作很出色,但生活上不很适应,甚至自杀未遂。多亏哈代的努力,使他受到了学术界的尊敬。一战结束后,拉马努金因为不习惯英国的生活,回到了印度,与母亲、妻子团聚,但家里也是矛盾重重。因为疾病,这位传奇人物于1920年去世,年仅33岁,临死前仍在写写划划。在当时拉马努金就已成为印度的一面旗帜,鼓舞了无数年轻人(后来印度出现了不少诺贝尔奖获得者)。
#7楼回目录拉马努金奖
捧心西子 | 2013-01-05 17:10
拉马努金是位富有传奇色彩的印度怪才数学家。当年哈代慧眼识珠的故事,为数学史增添荣光。 我喜欢哈代的一句话:他看到拉马努金写来的满是奇特数学公式的信,起初认为这应当又是一个民间数学骗子,但转念一想:有本事造出这类公式的骗子比数学天才更为罕见。 至于拉马努金,出生于印度南部,信奉婆罗门教。他应当是“数感”最好的诠释者:有一次Hardy去医院看望他,抱怨自己搭乘的出租车号码为1729:“是个乏味透顶的数字,是个不好的预兆。”拉马努金安慰他:“不是的,先生,事实上它很有趣――它是可用两种方法表为两数立方和的最小自然数。”
现在国际上主要有两项拉马努金为名的奖:SASTRA Ramanujan Prize和The Ramanujan Prize。 SASTRA Ramanujan Prize由拉马努金故乡的Shanmugha Arts, Science, Technology&Research Academy在2005年创立,颁发给与拉马努金有相同数学兴趣的杰出数学家。拉马努金的天才与寿命成反比,32岁即辞世,因此SASTRA特意将获奖者的年龄限制在32岁。2006年的获奖者,是我们都听说过的陶哲轩。 至于The Ramanujan Prize是ICTP于2005年创立的,颁发给发展中国家的优秀数学家。获奖者的年龄限制在相对宽松45岁,但总体看来这奖以Ramanujan为名是很匪夷所思的事情(另外,ICTP,不就是国际理论物理中心,实在与一项数学奖扯不上关系)。但这项奖的评奖委员会由IMU(是International Mathematical Union,不是Inner Mongolia University)成员组成,算是很有权威性的;并且奖金为15,000美元,和SASTRA的10,000美元比起来更为慷慨。清华数学中心访问学者张伟荣获2010 SASTRA Ramanujan奖。
#8楼回目录拉马努金百年秘神数函被解
捧心西子 | 2013-01-05 17:10
据国外媒体报道,1920年,印度数学天才斯里尼瓦瑟-拉马努金在临终前提出一系列数学函数。不幸的是,这些函数直到他死后近100年才得到证实。研究人员表示拉马努金提出的函数可用于解释黑洞的行为。
1920年,拉马努金在临终前给他的导师――英国数学家G. H。哈代写了一封信,概述几个此前从未听说过的新数学函数。他自称在梦中想出这些函数,对它们的特性存在强烈的直觉。几十年后,美国研究人员证明了拉马努金所提出数学函数的正确性,可用于解释黑洞的行为。美国埃默里大学数学家肯-小野表示:“我们破解了他最后几封神秘信件中的问题。对于数学领域的研究人员来说,这个问题存在了90多年。”
拉马努金是一位自学成才的数学家,出生在印度南部的一个村落,曾两次从大学辍学。他的大部分时间都在思考数学问题。拉马努金在信中阐述了几个新的数学函数,与已知的θ函数或者模形式不同,但又是对它们的一种极为接近的模拟。拉马努金提出的函数能够以轴线图表的形式表示,例如正弦波,可针对任何选定的值进行计算。
拉马努金指出他的模拟模形式与卡尔-雅可比早期确定的普通模形式相一致,可产生类似的结果。拉马努金是一位虔诚的印度教教徒,他认为这些函数是娜玛卡尔女神给他的启示。不幸的是,当时没有人能够理解他提出的函数。小野表示:“直到2002年我们才通过的桑德尔-泽维格斯的研究了解拉马努金在1920年的信件中描述的函数。”
小野和他的同事利用现代数学研究工具证明拉马努金的理论是正确的。这些研究工具是拉马努金所处时代所没有的。小野说:“我们证明拉马努金是对的。我们发现了他用于阐述自己理论的方程式。他相信之所以想出这个方程式是因为受到神灵的启示。”
此外,研究人员还吃惊地发现拉马努金提出的函数至今仍具有应用价值。小野说:“在拉马努金首次提出模拟模形式的上世纪20年代,还没有一个人讨论黑洞问题。不过,他提出的函数可用于揭示黑洞的秘密。毫无疑问,拉马努金为我们留下了一份宝贵遗产。”在11月于佛罗里达州立大学举行的纪念拉马努金诞辰125周年的会议上,研究人员公布了他们的研究发现。12月22日是拉马努金诞辰125周年。
 爱华网
爱华网