《初一几何证明题》证明书
初一几何证明题一、
1)D是三角形ABC的BC边上的点 且CD=AB,角ADB=角BAD,AE是三角形ABD的中线,求证AC=2AE。
(2)在直角三角形ABC中,角C=90度,BD是角B的平分线,交AC于D,CE垂直AB于E,交BD于O,过O作FG平行AB,交BC于F,交AC于G。求证CD=GA。
延长AE至F,使AE=EF。BE=ED,对顶角。证明ABE全等于DEF。=》AB=DF,角B=角EDF角ADB=角BAD=》AB=BD,CD=AB=》CD=DF。角ADE=BAD+B=ADB+EDF。AD=AD=》三角形ADF全等于ADC=》AC=AF=2AE。
题干中可能有笔误地方:第一题右边的E点应为C点,第二题求证的CD不可能等于GA,是否是求证CD=FA或CD=CO。如上猜测准确,证法如下:第一题证明:设F是AB边上中点,连接EF角ADB=角BAD,则三角形ABD为等腰三角形,AB=BD;∵ AE是三角形ABD的中线,F是AB边上中点。∴ EF为三角形ABD对应DA边的中位线,EF∥DA,则∠FED=∠ADC,且EF=1/2DA。∵ ∠FED=∠ADC,且EF=1/2DA,AF=1/2AB=1/2CD∴ △AFE∽△CDA∴ AE:CA=FE:DA=AF:CD=1:2AC=2AE得证第二题:证明:过D点作DH⊥AB交AB于H,连接OH,则∠DHB=90°;∵ ∠ACB=90°=∠DHB,且BD是角B的平分线,则∠DBC=∠DBH,直角△DBC与直角△DBH有公共边DB;∴ △DBC≌△DBH,得∠CDB=∠HDB,CD=HD;∵ DH⊥AB,CE⊥AB;∴ DH∥CE,得∠HDB=∠COD=∠CDB,△CDO为等腰三角形,CD=CO=DH;四边形CDHO中CO与DH两边平行且相等,则四边形CDHO为平行四边形,HO∥CD且HO=CD∵ GF∥AB,四边形AHOF中,AH∥OF,HO∥AF,则四边形AHOF为平行四边形,HO=FA∴ CD=FA得证
有很多题(散文阅读:www.www.AihuAu.com.net )
1.已知在三角形ABC中,BE,CF分别是角平分线,D是EF中点,若D到三角形三边BC,AB,AC的距离分别为x,y,z,求证:x=y+z
证明;过E点分别作AB,BC上的高交AB,BC于M,N点.
过F点分别作AC,BC上的高交于P,Q点.
根据角平分线上的点到角的2边距离相等可以知道FQ=FP,EM=EN.
过D点做BC上的高交BC于O点.
过D点作AB上的高交AB于H点,过D点作AB上的高交AC于J点.
则X=DO,Y=HY,Z=DJ.
因为D 是中点,角ANE=角AHD=90度.所以HD平行ME,ME=2HD
同理可证FP=2DJ。

又因为FQ=FP,EM=EN.
FQ=2DJ,EN=2HD。
又因为角FQC,DOC,ENC都是90度,所以四边形FQNE是直角梯形,而D是中点,所以2DO=FQ+EN
又因为
FQ=2DJ,EN=2HD。所以DO=HD+JD。
因为X=DO,Y=HY,Z=DJ.所以x=y+z。
2.在正五边形ABCDE中,M、N分别是DE、EA上的点,BM与CN相交于点O,若∠BON=108°,请问结论BM=CN是否成立?若成立,请给予证明;若不成立,请说明理由。
当∠BON=108°时。BM=CN还成立
证明;如图5连结BD、CE.
在△BCI)和△CDE中
∵BC=CD, ∠BCD=∠CDE=108°,CD=DE
∴ΔBCD≌ ΔCDE
∴BD=CE , ∠BDC=∠CED, ∠DBC=∠CEN
∵∠CDE=∠DEC=108°, ∴∠BDM=∠CEN
∵∠OBC+∠ECD=108°, ∠OCB+∠OCD=108°
∴∠MBC=∠NCD
又∵∠DBC=∠ECD=36°, ∴∠DBM=∠ECN
∴ΔBDM≌ ΔCNE ∴BM=CN
3.三角形ABC中,AB=AC,角A=58°,AB的垂直平分线交AC与N,则角NBC=( )
3°
因为AB=AC,∠A=58°,所以∠B=61°,∠C=61°。
因为AB的垂直平分线交AC于N,设交AB于点D,一个角相等,两个边相等。所以,Rt△ADN全等于Rt△BDN
所以 ∠NBD=58°,所以∠NBC=61°-58°=3°
4.在正方形ABCD中,P,Q分别为BC,CD边上的点。且角PAQ=45°,求证:PQ=PB+DQ
延长CB到M,使BM=DQ,连接MA
∵MB=DQ AB=AD ∠ABM=∠D=RT∠
∴三角形AMB≌三角形AQD
∴AM=AQ ∠MAB=∠DAQ
∴∠MAP=∠MAB+∠PAB=45度=∠PAQ
∵∠MAP=∠PAQ
AM=AQ AP为公共边
∴三角形AMP≌三角形AQP
∴MP=PQ
∴MB+PB=PQ
∴PQ=PB+DQ
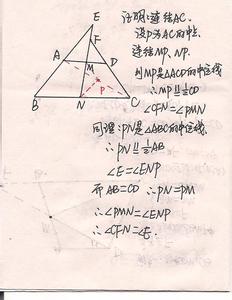
5.正方形ABCD中,点M,N分别在AB,BC上,且BM=BN,BP⊥MC于点P,求证DP⊥NP
∵直角△BMP∽△CBP
∴PB/PC=MB/BC
∵MB=BN
正方形BC=DC
∴PB/PC=BN/CD
∵∠PBC=∠PCD
∴△PBN∽△PCD
∴∠BPN=∠CPD
∵BP⊥MC
∴∠BPN+∠NPC=90°
∴∠CPD+∠NPC=90°
∴DP⊥NP。
 爱华网
爱华网